Определение. Пусть даны две плоскости комплексных чисел: плоскость Z точек z = x + i y и плоскость W точек 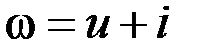 υ, где x, y, u, υ - действительные переменные.
υ, где x, y, u, υ - действительные переменные.
Рассмотрим некоторое множество точек М в плоскости Z и множество D в плоскости W.
Если каждому значению z Î М по какому-то закону поставлено в соответствие значение другого комплексного переменного w Î D, то говорят, что на множестве М определена функция комплексной переменной z и пишут
| y |
| υ |
| Z |
| x |
| u |
| W |
| O |
| z |
| w |
| M |
| D |
Так как z = x + i y, 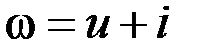 υ, то функция f (z) может быть записана в виде
υ, то функция f (z) может быть записана в виде
f (z) = u (x, y) + i υ (x, y),
u = Re f (z), υ = Im f (z).
Определение. Функция w = f (z) называется однозначной, если каждому значению z Î М можно поставить в соответствие только одно значение w ÎD, в противном же случае функция w = f (z) называется многозначной.
Будем откладывать значения z на одной комплексной плоскости, а значения w- на другой.
Тогда функцию комплексного переменного можно геометрически представить как отображение множества М плоскости Z на множество D плоскости W.
Пусть функция w = f (z) однозначна на множестве М и двум различным точкам М всегда соответствуют различные точки D, то такое отображение принято называть взаимно однозначным или однолистным.
Точки множества D называют образами соответствующих точек множества М при отображении
w = f (z),
а точки множества М – прообразами соответствующих точек множества D.
Определение. Область, ограниченная замкнутой несамопересекающейся линией называется односвязной.
К односвязным областям принадлежит вся плоскость. Другие примеры односвязных областей приведены на рисунке. Сами области заштрихованы. Если граница области входит в область задания, то она изображается сплошной линией, если нет - пунктиром.
Ограниченная замкнутая область Ограниченная открытая область
| у |
| х |
| О |
| у |
| х |
| О |
Определение. Область называется двусвязной, если она ограничена двумя замкнутыми непересекающимися и несамопересекающимися линиями.
К примеру, область будет двусвязной, если внутри рассматриваемой части плоскости имеется одна точка или односвязная ограниченная область, не принадлежащая к области задания функции.
Двусвязные области:
| у |
| х |
| О |
Ограниченная двусвязная область
| у |
| х |
| J |
Многосвязные области:
Трехсвязная область Четырехсвязная область
| у |
| х |
| О |
| у |
| х |
| О |
| z 1= i |
| х |
| О |
Производная функции
Комплексного переменного.
Определения, формулы и теоремы в изучении производной и дифференциала функции комплексного переменного практически полностью совпадают с аналогичными определениями, формулами и теоремами в случае действительного переменного. Но дифференцируемые функции комплексного переменного по сравнению с дифференцируемыми функциями действительного переменного обладают многими дополнительными свойствами.
Определение. Пусть однозначная функция w =f (z) определена в точке z и ее окрестности.
Производной функции f (z) в точке z называется предел отношения приращения функции к приращению аргумента, если такой предел существует:
 (15.18)
(15.18)
В формуле (15.18) D z стремится к нулю по любому закону (по любому пути). Точка z +D z может приближаться к точке z по любому из бесконечного множества различных лучей и для существования производной для функции f (z) комплексного переменного требуется совпадение всех этих пределов.
| (В случае функции действительного переменного, если функция y=f (x) имеет производную, это означает, что существует предел |
отношения 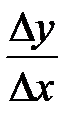 при стремлении точки х+ D х к точке х только по двум направлениям: справа (D х >0) и слева (D х <0) и эти пределы совпадают.)
при стремлении точки х+ D х к точке х только по двум направлениям: справа (D х >0) и слева (D х <0) и эти пределы совпадают.)
Функция, которая имеет производную в данной точке, называется дифференцируемой, а также моногенной или голоморфной в этой точке.
Аналитические функции
Основное содержание общей теории комплексного переменного составляет теория аналитических функций.
Известны различные подходы к понятию аналитичности. Один из них, тесно связанный с геометрическими представлениями, впервые был освещен в работах О. Коши, затем развит в трудах Б. Римана. В его основе лежит так называемое структурное свойство функции – существование производной по комплексному переменному.
Другой подход, связанный с аналитическим аппаратом, которым может быть изображена функция, основан на возможности представления функций степенными рядами. Этот подход был развит в работах К. Вейерштрасса.
Определение. Функция  , определенная в области D, называется аналитической (голоморфной) в точке
, определенная в области D, называется аналитической (голоморфной) в точке 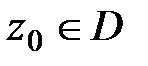 , если существует некоторая окрестность этой точки, в которой функция
, если существует некоторая окрестность этой точки, в которой функция  может быть представлена степенным рядом
может быть представлена степенным рядом
 .
.
Функция  называется аналитической (голоморфной) в области D, если это свойство выполняется в каждой точке
называется аналитической (голоморфной) в области D, если это свойство выполняется в каждой точке  этой области.
этой области.
Как указывалось ранее, функция  , голоморфная в точке
, голоморфная в точке 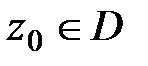 , дифференцируема в этой точке.
, дифференцируема в этой точке.
Голоморфность функции  в области означает, что в каждой точке этой области функция
в области означает, что в каждой точке этой области функция  бесконечно дифференцируема и ее ряд Тейлора сходится к ней в некоторой окрестности этой точки.
бесконечно дифференцируема и ее ряд Тейлора сходится к ней в некоторой окрестности этой точки.






