проецирующей в плоскость уровня
Алгоритм графических построений:
Проводим первую ось вращения i;
В треугольнике АВС проводим горизонталь C2M2 и находим ее проекцию на П1;
Поворачиваем A1B1C1 вокруг оси i до положения, при котором C1M1 будет перпендикулярен оси проекций П1П2;
A1'B1'C1' - горизонтальная проекция после первого поворота;
Параллельно оси проекций проводим фронтальные проекции дуг, по которым двигаются точки А В С на П2. На чертеже это вспомогательные линии серого цвета;
Из A1'B1'C1' проводим линии проекционной связи до пересечения с соответствующими проекциями дуг. A2'B2'C2' - новая фронтальная проекция АВС после первого поворота. a - искомый угол наклона плоскости АВС к П1;
Проводим ось j через точку В';
Поворачиваем A2'B2'C2' до положения параллельного оси проекций. A2"B2"C2" - фронтальная проекция АВС после второго поворота;
Параллельно оси проекций проводим горизонтальные проекции дуг, по которым двигаются точки А В С на П1. На чертеже это вспомогательные линии серого цвета;
Из A2"B2"C2" проводим линии проекционной связи до пересечения с соответствующими проекциями дуг. A1"B1"C1" - новая горизонтальная проекция треугольника АВС в натуральную величину после второго поворота.
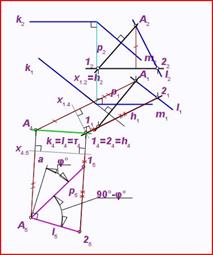
Определение угла между прямой и плоскостью
Углом между прямой и плоскостью является линейный угол между пересекающимися прямыми, проведенными параллельно заданным. Задача 61
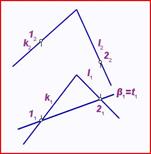
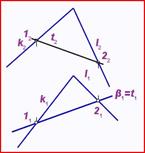
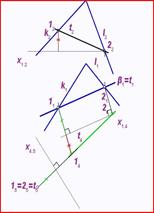
Определение угла между плоскостями
Углом между двумя плоскостями называется один из двух смежных двугранных углов между этими плоскостями.
задача 62
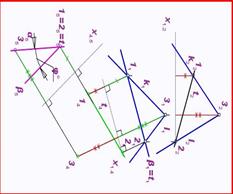
Кривые линии. Классификация кривых линий
Кривая линия - это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по-разному.
В начертательной геометрии кривую рассматривают как траекторию, описанную движущей точкой, как проекцию другой кривой, как линию пересечения двух поверхностей, как множество точек, обладающих каким-либо общим для всех их свойством и т.д.
Например, (рис.80) циклоида – траектория движения точки окружности, катящейся без скольжения по прямой линии. Эта кривая состоит их ряда «арок», каждая из которых соответствует полному обороту окружности.
1. Парабола
2. Эллипс
3. Синусоида
4. Гипербола
Задача 69
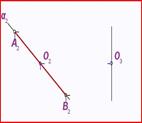
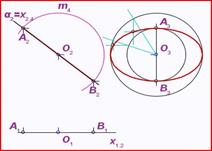
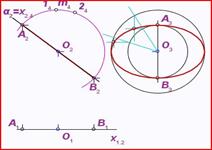
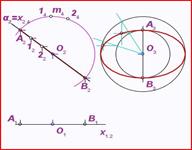
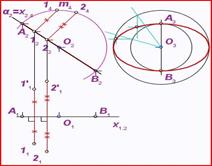
Поверхность
Поверхность можно рассматривать, как совокупность последовательных положений l1,l2… линии l перемещающейся в пространстве по определенному закону (рис.93). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму - изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в одной линии или целого семейства линий (m, n, p...). Подвижную линию принято называть образующей, неподвижные - направляющими. Такой способ образования поверхности принято называть кинематическим.
По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.
Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.
Если же группировать поверхности по закону движения образующей линии и производящей поверхности, то большинство встречающихся в технике поверхностей можно разделить на:
· поверхности вращения;
· винтовые поверхности;
· поверхности с плоскостью параллелизма;
· поверхности параллельного переноса.
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают ее форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).
Для графического изображения поверхности на чертеже используется её каркас.
Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности.
Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом.
Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.
Различают две части определителя: геометрическую и алгоритмическую.
Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.
Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.
Определитель кривой поверхности - направляющие и образующие.
20. Поверхности вращения и их задание на чертеже
Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси
Геометрическая часть определителя состоит из двух линий: образующей m и оси i
Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Из закона образования поверхности вращения вытекают два основных свойства:
1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.
2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум
симметричным относительно оси линиям – меридианам.
Плоскость, проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.
Сфера – образуется вращением окружности вокруг её диаметра.
При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг малой оси, то эллипсоид называется сжатым или сфероидом, если вокруг большой – вытянутым.
Тор – образуется при вращении окружности вокруг оси, не проходящей через центр окружности
Параболоид вращения – образуется при вращении параболы вокруг своей оси
Гиперболоид вращения – различают одно и двух полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.
