Этот способ является частным случаем способа плоскопараллельного перемещения, когда точка фигуры описывает дугу окружности, плоскость которой также параллельна плоскости проекций.
Графический алгоритм построения точек в способе вращения вокруг проецирующей прямой отличается лишь тем, что здесь траектория движения точки имеет вид окружности, а не произвольной прямой, как в плоскопараллельном проецировании.
Способ вращения вокруг проецирующей прямой более удобен при решении некоторых задач. Найдем с применением этого метода длину отрезка AB. Отрезок AB спроецируется на П2 в натуральную величину, если он будет ей параллелен. Для этого повернем его вокруг оси, проходящей через точку B до состояния параллельности П2, при этом точка A опишет дугу в горизонтальной плоскости.
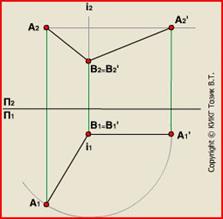
Алгоритм графических построений:
Проведем ось вращения i через точку B. Ось i перпендикулярна П2;
Повернем отрезок AB до состояния параллельности оси проекций П1П2. Где A1'B1' - новая проекция AB;
Проводим вспомогательную линию на П2. Эта линия символизирует горизонтальную плоскость, в которой поворачивалась точка A;
Проводим линию связи и находим новую проекцию A2'B2' отрезка AB на П2;
A2'B2' - натуральная величина отрезка AB.
1) натуральную величину отрезка к Я,;
2) натуральную величину треугольника ABC. А В и угол наклона
|
13. Взаимное положение прямой и плоскости (параллельная и перпендикулярная прямая)
Параллельная
При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой плоскости.
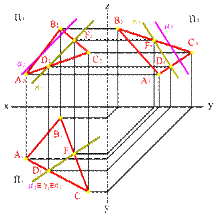
Задача. Дано: плоскость общего положения ABC и прямая общего положения а.
Требуется оценить их взаимное положение (рис.59).
Для этого через прямую а проведем вспомогательную секущую плоскость g - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей g и АВС - прямую п (DF). Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а1 и со следом плоскости g. Проекция прямой п2 параллельна а2, п3 параллельна а3, следовательно, прямая а параллельна плоскости AВС.
Перпендикулярная
Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.
Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.
Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n1^h1. Аналогично для фронтали – f^n Þ f2^ n2.
Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.
Доказательство следует из теоремы о проецировании прямого угла.
Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.61).
Задача. Дано: плоскость ВСD и точка А.
Требуется построить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.
В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А1 прямую n1 перпендикулярно горизонтальной проекции горизонтали h1, а на фронтальной плоскости проекций через точку А2 прямую n2 перпендикулярно фронтальной проекции фронтали f2, согласно, теореме о перпендикуляре к плоскости, полученная прямая n будет перпендикулярна плоскости ВСD.
