Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла).
|
|

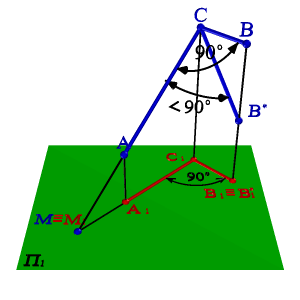
Дано: Ð АВС = 90о; [ВС] // П1; [АС] # П1.
Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П1 (рис. 39) получим горизонтальный след прямой - точку М º М1, одновременно принадлежащую прямой и ее проекции. Из условия следует, что [ВС] // [В1С1]. Если через точку М проведем прямую МD параллельную С1В1, то она будет параллельна и СВ, а следовательно Ð СМD= 90о. Согласно теореме о трех перпендикулярах Ð С1МD=90о. Таким образом, [MD]^[А1С1] и [MD]//[В1С1], следовательно, Ð А1С1В1= 90о, что и требовалось доказать. В случае, когда [АС]^П1 проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.
2. Если проекция угла представляет угол 900, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций (рис. 40).
3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу.
4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.
5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением.
7. Метод прямоугольного треугольника и его использование на двухкартийном чертеже
Длину отрезка АВ и a - угол наклона отрезка к плоскости П1 можно определить из прямоугольного треугольника АВС |AС|=|A1B1|, |BС|=DZ. Для этого на эпюре (рис.31) из точки B1 под углом 900 проводим отрезок |B1B1*|=DZ, полученный в результате построений отрезок A1B1* и будет натуральной величиной отрезка АВ, а угол B1A1B1*=a. Рассмотренный метод называется методом прямоугольного треугольника. Тот же результат можно получить при вращении треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций».

Длину отрезка АВ и b-угол наклона отрезка к плоскости П2 можно определить из прямоугольного треугольника АВС |AС|=|A2B2|, |BС|=DY. Построения аналогичные рассмотренным, только в треугольнике АВВ* сторона |BВ*|=DU и треугольник совмещается с плоскостью П2








