Þ 
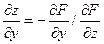(12)
Пр. exp z + xy + zx = 0; ¶z/¶x =?, ¶z/¶y =?. Пусть F(x,y,z) = exp z + xy + zx,
тогда ¶F/¶x = y + z; ¶F/¶y = x; ¶F/¶z = exp z + x и по формулам (11),(12) имеем
¶z/¶x = - (y + z)/(exp z + x); ¶z/¶y = - x / (exp z + x)
Кривые в пространстве.
Дифференциальная геометрия изучает линии и поверхности в пространстве методами дифференциального исчисления и использует для их описания непрерывные функции.
Линию L в пространстве можно задать параметрическим уравнением: x = x(t), y = y(t), z = z(t), где x, y, z – координаты точки линии М и t1 < t < t2 или векторным уравнением 
= (t) = x(t) i + y(t) j + z(t) k, т.к. каждой точке M(x,y,z) кривой L соответствует радиус-вектор 
= = x i + y j + z k.
К каждой точке кривой можно провести касательную прямую и ее направление легко определить из векторного уравнения. Производной от векторной функции = (t) по t
наз. вектор ’(t) = lim 
/ t = lim [ (t + t) – (t) ] / t =
t 
0 t 0
= x’(t) i + y’(t) j + z’(t) k (13)
Разность векторов (t+ t) – (t) = – 
= 
определяет секущую прямую, проходящую через точки кривой М и М0 . При t 0 М М0 и секущая превращается в касательную, направление которой задает вектор ’ = {x’(t), y’(t), z’(t)} 
.
Зная направляющий вектор касательной и точку приложения, легко построить уравнение касательной к L. Пусть M(x,y,z)произвольная точка касательной, проходящей через точку кривой M0 (x0, y0, z0). Тогда направляющий вектор касательной ={x’(t0), y’(t0), z’(t0)} коллинеарен вектору и условие их коллинеарности = 
превращается в каноническое уравнение касательной к кривой L в точке М0
(x – x0) / x`(t0) = (y – y0) / y`(t0) = (z – z0) / z`(t0) (14)
Плоскость пересекающая кривую L в точке М0 и перпендикулярная касательной к кривой в этой точке, наз. нормальной плоскостью. Пусть М(x,y,z) произвольная точка плоскости, тогда вектор лежит в этой плоскости и перпендикулярен вектору . Из условия их перпендикулярности = 0 получаем уравнение нормальной плоскости
(x – x0) x`(t0) + (y – y0) y`(t0) + (z – z0)z`(t0) = 0 (15)
Пр. Написать уравнение касательной и нормальной плоскости к винтовой линии L: x = 2 cos t, y = 2 sin t, z = t/ 
при t = /4
Еще используют следующие локальные параметры кривой: | r``(t) | = K – кривизна кривой в точке; R = 1/K - радиус кривизны; кручение T – выражается через первые три производные.
Поверхности в пространстве.
Способы задания:
· явная форма - z = f(x,y), (x,y) Î D – уравнение гладкой поверхности. Каждой точке (x,y) соответствует одно значение z. Поверхность однослойная, двухсторонняя;
· неявная форма - F(x,y,z) = 0, (x,y,z) Î V – общее уравнение поверхности. Точке (x,y) может соответствовать несколько значений z. Замкнутые поверхности;
· параметрическая форма – x = x(u,v), y = y(u,v), z = z(u,v), (u,v) Î D. Переход от одного к двум параметрам приводит к множеству линий, которые формируют поверхность. Пр. На сфере радиуса r параметры u, v это широта и долгота точки.;
· векторная форма = (u,v), (u,v) ÎD.
Опр. Касательной плоскостью к поверхности F(x,y,z) = 0 в точке M0 (x0, y0, z0) наз. плоскость, в которой расположены касательные ко всем линиям, лежащим на поверхности и проходящим через т. М0.
Пусть некоторая линия L проходит по поверхности F(x,y,z) = 0 через точку M0 (x0, y0, z0). Ее уравнение дано в векторной форме = (t) и = {x’(t0), y’(t0), z’(t0)} -направляющий вектор касательной к кривой в т. M0. Объединим оба уравнения F(x(t),y(t),z(t)) = 0, получим функцию зависящую от параметра t и продифференцируем её
= 0
По своей структуре это выражение соответствует условию ^ двух векторов: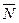 
= 0,
где вектор 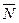= {¶F/¶x, ¶F/¶y, ¶F/¶z } (16)
определяется только свойствами поверхности. Т.к. линия L произвольна, то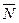 
к касательным всех линий, проходящих через т. М0 по поверхности и, следовательно, вектор 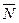(16) является нормальным вектором касательной плоскости к этой точке, при условии, что частные производные от F(x,y,z) существуют, непрерывны и не равны нулю одновременно.
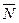Пусть M(x,y,z) произвольная точка касательной плоскости. Тогда вектор лежит на плоскости и . У словие перпендикулярности 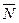= 0 приводит к уравнению касательной плоскости
(x – x0) (¶F/¶x) + (y – y0) (¶F/¶y) + (z – z0) (¶F/¶z) = 0 (17)
где частные производные вычислены для точки М0
Нормалью к поверхности в точке М0 наз. прямая касательной плоскости к этой точке. Направляющим вектором нормали является вектором 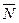, который коллинеарен любому отрезку прямой . Условие их коллинеарности = приводит к каноническому уравнению нормали
(x – x0) /(¶F/¶x) = (y – y0) / (¶F/¶y) = (z – z0) / (¶F/¶z) (18)
Пр. Записать уравнения касательной плоскости и нормали к поверхности
x2 – y2 – z = 0 в т. М(1,1,2).
Решение: (¶F/¶x)М = (2х)М = 2, (¶F/¶y)М = - 2, (¶F/¶z)М = - 1
Уравнение касательной плоскости: 2(х – 1) – 2(y – 1) – (z – 2) = 0
Уравнение нормали: (x – 1) / 2 = (y – 1) / -2 = (z – 2) / -1
Экстремумы ФНП.
Опр. Точка. M 0 (x0, y0) наз. точкой MIN функции z = f(x,y), если для любых точек из ближайшей 
- окрестности М0 выполняется неравенство f(x,y) > f(x0, y0). Точка MAX определяется обратным неравенством f(x,y) < f(x0, y0).
Поверхность вблизи экстремальной точки имеет вид чаши. Рассмотрим плоскость сечения проходящую через точку MIN (х0, у0) | | оси O z с нормальным вектором 
={ P; Q; 0 }:
P(x – x0) + Q(y – y0) = 0 или y = -P/Q x + b,(19)
где координаты P, Q произвольны. Плоскость пересекает ось О х под углом 
, причем, tg = -P/Q. Линия пересечения плоскости сечения с поверхностью z = f(x,y) имеет экстремум в т. (х0, у0) при любом значении .
Необходимое условие экстремума. Если функция z = f(x,y) имеет экстремум в точке М, то ее частные производные в т. М или обращаются в ноль или не существуют. Условие
(¶z/¶x)M = 0, (¶z/¶y)M = 0 (20)
определяет стационарную точку, подозрительную на экстремум, и означает, что линии пересечения поверхности плоскостями х = х0, у = у0, т.е. при = 900 и = 00 , имеют экстремумы в т. М по теореме Ферма.
Пр. z = x2 – y2. Условия ¶ z /¶ x = 2 х =0, ¶ z /¶ у = 2 у =0 определяют стационарную точку (0, 0), которая экстремальной не является, т.к. при у = 0 имеем min параболы z = x2, а при х = 0 имеем max параболы z = – y2.
Необходимо проверять на экстремум линии сечения поверхности плоскостями сечения при произвольном угле .
Достаточное условие экстремума. Пусть плоскость сечения проходит через точку min (x0, y0) и точку (x0 + dx, y0 + dy), где выбор величин dx, dy произволен. Плоскость пересекает ось О х под углом , где tg 
= dy/dx,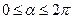 
. При этом приращение функции z = dz + ½ d2z +.. > 0. Однако, это условие сразу упрощается: d2z > 0, т.к. dz = (¶z/ ¶x)М dx + (¶z/ ¶y)М dy = 0. Введем обозначения А = ¶ 2z/ ¶x2, В = ¶ 2z/ ¶x¶y, С = ¶ 2z/ ¶y2, тогда по формуле(6) d2z = Adx2 + 2Bdxdy + Cdy2. Т.к. величины dx, dy могут менять свой знак, то условиеmin: d2z > 0 для любых , будет выполняться только при некоторых ограничениях на А, В, С. Определим их.
Дифференциалы dx, dy образуют прямоугольник с диагональю 
и dx = 
cos , dy = sin . В полярных координатах
d2z = 
2(A cos2 + 2B cos sin + C sin2 ) = 2sin2 (At2 + 2Bt + C) > 0,
где t = ctg . Исследуем неравенство At2 + 2Bt + C = А(t – t1)(t – t2) > 0. Если дискриминант B2 – AC > 0 икорни t1, t2 действительные числа, то знак трехчлена меняется при изменении угла : d2z > 0 при t < t1 и t > t2,а при t1 < t < t2 d2z < 0. Т.е. условие экстремума – постоянство знака d2z при любом не выполняется. В случае отрицательного дискриминанта АС – В2 = (М) > 0 основной вклад в трехчлен уже вносят члены с постоянным знаком At2, C; корни комплексные и условие постоянства знака для d2z выполняется. Значение знака определяет вторая производная AM. В результате имеем
1) (M)> 0, AM > 0 - условие MIN в т. М.; 2) (M)> 0, AM < 0 - условие MAX в т.М;
3) (M)< 0 -экстремума нет; 4) (M) = 0 – требуется дополнительное исследование.
Пр. Исследовать на экстремум функцию z = 2 x3 + xy2 + 5x2 + y2 , (x,y) 
R2
z’x = 6x2 + y2 + 10x = 0; z’y = 2y(x + 1) = 0. Если y =0, то 6x2 + 10x =0 или x =0, x = -5/3.
Если x = -1, то y2 – 4 = 0 или x =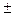 
2. 
M1(0,0); M2(-5/3, 0); M3(-1,-2); M4(-1,2)
A = z’’xx = 12x + 10, B = z’’xy = 2y, C = z’’yy = 2(x + 1), (АС – В2) = (М)
1. (M1) = 20>0, AM = 10>0 MIN 2. (M2) = 40/3, AM = -10<0 MAX
3. (M3) = -16<0 - экстремума нет 4. (M4) = -16<0 - экстремума нет 
Условный экстремум ФНП.
Задача. Найти экстремумы функции z = f(x,y) при условии, что F(x,y) = 0.
Пр.1 Найти длины сторон прямоугольника, имеющего наибольшую площадь S = xy при заданной величине его периметра p =2x + 2y.
Условие F(x,y) = 0 также наз. уравнением связи. Геометрически оно определяет некоторую цилиндрическую поверхность в пространстве, которая пересекается с поверхностью z = f(x,y) по некоторой линии. Фактически необходимо исследовать на экстремум эту линию пересечения.
Главная идея решения – использовать уравнение связи для уменьшения числа переменных в исходной функции. Возможны два случая.
А) Уравнение связи имеет явный вид y = g(x). Тогда сразу переходим к функции одной переменной z = f(x, g(x)) и исследуем ее обычным образом
Пр.1 S = xy; p =2x + 2y y = x – p/2, S = x (x – p/2) S’ = 2x – p/2 = 0, x = p/4
Б) Уравнение связи имеет неявный вид F(x,y) = 0. Тогда задача решается методом множителей Лагранжа.
Определим те условия, которые накладываются на функции f(x,y), F(x,y) факт существования в точке М (x 0, y 0)условного экстремума.
Пусть F(x,y) имеет непрерывные частные производные в точке M и Fy’ 
0. Из уравнения связи F(x,y) = 0 следует dF = 0 и dF/dx = 0, кроме того,фактически f(x,y) зависит только от х и поэтому в точке экстремума df/dx = 0. Запишем полные дифференциалы функций f(x,y), F(x,y) в точке M и разделим их на dx.
df / dx = (fx’ + fy’ dy/dx)|M = 0
dF / dx = (Fx’ + Fy’ dy/dx) |M = 0
Из этой системы уравнений исключим неизвестную нам производную dy/dx |M. Для этого умножим нижнее уравнение на число и прибавим его к верхнему уравнению. Число определим из условия (fy’ + Fy’)|M = 0. В результате получаем, что в точке условного экстремума М (х0, у0) должны выполняться следующие соотношения
(fx’ + Fx’)|M = 0; (fy’ + Fy’)|M = 0; F(x0, y0) = 0
Их можно использовать для определения координаты точки условного экстремума, решив эту систему трех уравнений для x 0, y 0, .
Идея метода Лагранжа - задачу определения условного экстремума функции f заменить на задачу определения простого экстремума другой функции Ф.
Алгоритм метода множителей Лагранжа
1.Составляем функцию Лагранжа: Ф(x,y, ) = f(x,y) + F(x,y)
2.Вычисляем частные производные от Ф, приравниваем их к нулю (необходимое условие простого экстремума)
f ’x + F ’x = 0; f ’y + F ’y = 0; F(x, y) = 0
В результате получаем систему трех уравнений, которая определяет координаты точки условного экстремума для f(x,y).
3.Решаем систему этих уравнений, определяем и находим координаты точек экстремума, который для функции Ф(х,у, ) является простыми экстремумами, а для функции f(x,y) условными.
4.Проверим стационарные точки достаточным условием существования экстремума ФНП.
Пр.1. 1) Ф = xy + (p –2x – 2y); 2) Ф’x= y -2 = 0, Ф’y = x - 2 = 0, p = 2x + 2y
3) решение системы x = y = p/4, = p/8
Пр.2.Найти точки экстремума функции z = 9 – (x – 1)2 – (y –2)2, если уравнение связи y – x = 0. Рассмотрим оба способа решения.
Функция определяет параболоид вращения с вершиной в точке N(1,2,9), который пересекает плоскость у = х. Наша задача – исследовать на экстремум линию их пересечения.
Решение Б.
1) Составим функцию Лагранжа Ф = 9 – (x – 1)2 – (y –2)2 + (у – х)
2) Ф’x = - 2(x – 1) - = 0; Ф’y = - 2(y – 2) + = 0; Ф’ = (y – x) = 0
3) Решение системы уравнений: x = y = 3/2, = - 1
4) Ф’’xx = - 2 A; Ф’’xy = 0 B; Ф’’yy = - 2 C;
AC – B2 = 4 > 0, A = - 2 < 0 max в точке (3/2, 3/2, 8,5)
Решение А. Условие у = х приводит функцию к виду z = - 2 x2 + 6 x + 4. Исследуем ее на экстремум: z` = 6 – 4 x; 2) 6 – 4x = 0 x = 3/2; 3) z`` = - 4;4) z``( 3/2) = - 4 < 0 max; 5) z (3/2) = 8,5. Ответ: max в точке (3/2; 3/2; 8,5).
