Лк-3.
Сила тяжести – частный вид гравитационной силы. Величина гравитационной силы притяжения двух точечных масс m1 и m2 определена Ньютоном и известна как закон всемирного тяготения:
, (3.1)
где r - расстояние между массами, а G = 6,67 10 -11 Нм2/кг2 - гравитационная постоянная. В частности, для силы тяжести на поверхности земли:
(3.2)
Откуда определится формула для ускорения свободного падения:
Радиус земли известен Rземл=6380 км. Данная формула позволяет вычислить массу земли.
Динамика вращательного движения материальной точки
Рассмотрим ситуацию вращательного движения материальной точки с массой m вокруг оси, которую для определенности направим вертикально, как показано на рис. 2.5. Линейная скорость движения точки по окружности - v связана с угловой скоростью - ω формулой (2…)
Импульс точки 
. Назовем моментом импульса величину
(3.3)
Подставим в (2.14) вместо р его выражение через линейную скорость:
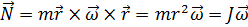(3.4)
Величина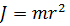 
называется моментом инерции материальной точки, а формула (3.4) по форме аналогична формуле импульса, в которую вместо массы точки подставлен ее момент инерции, а вместо скорости - угловая скорость. Продифференцируем по времени (3.4)
Первое слагаемое в правой части равно нулю, так как векторы импульса - р и скорости dr/dt параллельны. Во втором слагаемом производная от импульса, согласно второму закону Ньютона, представляет силу, действующую на точку. Следовательно
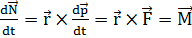(3.5)
Величина
(3.6)
называется моментом силы F относительно оси вращения. Таким образом, производная по времени от момента импульса равна моменту силы. Вновь получаем аналогию с поступательным движением, при котором производная по времени от импульса равна силе.
С другой стороны, взяв производную по времени от (3.4), получим
, где ε - угловое ускорение. Заменив dN/dt моментом силы, получим аналог второго закона Ньютона для вращательного движения:
(3.7)
Все формулы для вращательного движения материальной точки легко запомнить, поскольку по форме они аналогичны формулам поступательного движения. Необходимо только заменить массу на момент инерции, силу - на момент силы, скорость - на угловую скорость, импульс - на момент импульса.
| Поступательное движение | Вращательное движение |
| Масса m | Момент инерции j=mr2 |
Линейная скорость 
| Угловая скорость 
|
Линейное ускорение 
| Угловое ускорение 
|
Сила 
| Момент силы 
|
Импульс 
| Момент импульса 
|
Основное уравнение динамики 
| Основное уравнение динамики 
|
Пример: Качание тела, подвешенного на нити длиной l, является движением по окружности с центром в точке подвеса. Составить уравнение движения тела, используя в качестве координаты угол отклонения нити от вертикали. Поместим начало координат в точку подвеса - О. Координатой материальной точки будет угол α между нитью подвеса и вертикалью. Этот угол мы считаем векторной величиной, причем направлен этот вектор перпендикулярно плоскости рисунка от нас. В ту же сторону направим ось Z. Очевидно, что точка будет совершать колебательное движение по окружности с радиусом |r|. Составим уравнение движения. Само уравнение движения очень простое, его можно записать в форме (3.7). Однако, для этого необходимо выразить векторы момента силы и углового ускорения через данные задачи. Мы считаем данными длину нити подвеса |r|=l. Обозначим через m массу мат. точки.
Момент силы тяжести: 
Момент инерции J=m|r|2=ml2
Уравнение движения:
Подставим это в уравнение движения 
После сокращения на m приходим к выводу о том, что масса точки не влияет на характер движения.
При работе с векторами на какой-то стадии требуется переход к скалярным величинам. Этот переход осуществляется путем проецирования векторов на произвольно выбранную ось. Умножим левую и правую части векторного уравнения на единичный вектор оси, перпендикулярной плоскости рисунка.
Векторное произведение 
направлено против оси Z, поэтому 
. Вектор углового ускорения со направлен с осью Z, поэтому 
. В результате получим скалярное уравнение
Это и есть искомое уравнение движения. Его нужно сократить на l и вместо углового ускорения - ε подставить вторую производную по времени от угла α:
Если решить это уравнение, то мы получим зависимость угла α от времени. Из вида уравнения следует, что единственным параметром этой зависимости является отношение g/l.
Работа и энергия. Элементарной работой dA силы F на перемещении dl называется их скалярное произведение (см. рис):
(3.8)
В декартовой системе координат величину элементарной работы (по правилам записи скалярного произведения) можно записать в следующем виде:
dA=Fxdx+Fydy+Fzdz (3.9)
где Fx, Fy, Fz - проекции силы на оси координат и dx, dy, dz - cоответствующие проекции перемещения. Для подсчета работы переменной силы на конечном перемещении необходимо просуммировать все элементарные работы
Когда суммируются бесконечно много бесконечно малых слагаемых типа 
, вместо значка Σ используется значок ∫, а вместо индекса суммирования –i указываются начальная и конечная точки пути, например a и b. В результате запись формулы для работы примет следующий вид:
Размерность работы [Н*м] называется Джоулем: 1Дж=1Н*1м.
Пятиминутка. Человек везет сани, как показано на рисунке. Пройденный путь – 1 км, модуль приложенной силы 10 Н, угол α=60о. Вычислить совершенную работу.
Кинетическая энергия. Если на тело массы m действует некоторая сила F, сообщая ему ускорение - а, то эта сила совершает работу, которая связана с изменением скорости тела. Вычислим элементарную работы на участке траектории dl.
Поменяем местами множители в скалярном произведении:
Скалярное произведение v*dv представляет собой произведение модуля скорости - v на проекцию приращения скорости на направление вектора скорости. Эта проекция называется тангенциальным приращением скорости, которое равно увеличению ее модуля. Следовательно
Или так: 
. В данном случае v – это модуль скорости. Определим скалярную величину, производная от которой по модулю скорости равна mv, и назовоем ее кинетической энергией.
Эта величина называется кинетической энергией движущегося тела. Поскольку и 
, мы приходим к выводу о том, что dA=dWк. Элементарная работа, совершенная силой, разгоняющей материальную точку, перешла в приращение кинетическую энергию этой точки. Этот же вывод справедлив и на конечном участке траектории: работа, совершенная разгоняющей силой равна приращению кинетической энергии тела.
Пятиминутка. Тело массой 1 кг брошено горизонтально с начальной скоростью 50 м/с. Вычислить работу силы тяжести и кинетическую энергию в конце 2 секунды движения.
Потенциальная энергия. Во многих случаях сила, действующая на тело, оказывается зависимой от его положения, от координат тела. И величину силы вдоль координатной оси можно вычислить путем дифференцирования некоторой величины по этой координате.
(3.12)
В этом случае сила называется потенциальной, а величина U – потенциальной энергией тела.
Элементарная работа потенциальной силы
Т.е. равна убыли потенциальной энергии тела.
В качестве примера рассмотрим вычисление работы центральной силы, т.е. силы, которая действует по прямой, соединяющей два взаимодействующих тела (материальные точки), и величина этой силы зависит только от расстояния между ними.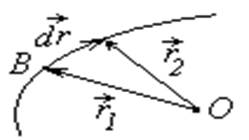 
Пусть материальная точка О действует на другую точку В центральной силой F. Точка В перемещается из положения 1 с радиусом-вектором r1 в близкую точку 2, радиус-вектор которой - r2 (см. рис.3.2). Перемещение точки В равно dr и формула для элементарной работы запишется в обычном виде:
Так как сила является центральной она направлена вдоль радиус-вектора, поэтому скалярные произведения и оказываются равными произведениям модулей силы и радиус-вектора. Тогда
(3.11)
где dr - приращение расстояния между взаимодействующими точками на малом участке траектории. Знак ± соответствует двум возможным знакам скалярного произведения Если вектор силы параллелен радиус-вектору, косинус угла между ними равен 1, ставится знак +. Это случай отталкивания между телами. Если же вектор анти параллелен радиус-вектору, угол между ними равен π, а косинус его равен -1. Этот случай соответствует притяжению между телами, ему соответствует знак -. Работа центральной силы на конечном участке траектории между точками 1-2 находится суммированием всех элементарных работ, с учетом того. что величина силы зависит от расстояния между телами, т.е.
(3.12)
где U(r) - потенциал силы.
Из (3.12) видно, что работа центральной силы не зависит от формы траектории и определяется только расстояниями между взаимодействующими мат. Поскольку ребота потенциальных сил не зависит от формы траектории, а определяется только положением начальной и конечной точки, работа потенциальной на траектории, где начальная и конечная точки совпадают, равна нулю.
Для силы тяготения земли, которая является центральной силой, работа при увеличении расстояния от земной поверхности от r1 до r2 согласно выражению (3.12) равна:
В частности, если r1=R3 - радиусу земли, а r2=∞, т.е. тело удаляется от земли в бесконечность, сила притяжения совершает работу
