for i:=1 to k do writeln(mr[i].tb:3,mr[i].ch:4); writeln; {вывод массива MR}
{----------------сортировка MR по табельному номеру-----------------------------}
for i:=1 to k-1 do begin;
for j:=i+1 to k do if mr[i].tb>mr[j].tb then
begin x:=mr[i]; mr[i]:=mr[j];mr[j]:=x end;
End;
{вывод отсортированного массива Работ}
for i:=1 to k do writeln(mr[i].tb:3,mr[i].ch:4); writeln;
{--обобщение записей с одинаковыми табельными номерами: для группы повторяющихся номеров в первой записи производится суммирование часов, в остальных – поле номера устанавливается в 0}
i:=1;
while i<k do begin
j:=1;
while mr[i].tb=mr[i+j].tb do begin
mr[i+j].tb:=0; mr[i].ch:=mr[i].ch+mr[i+j].ch; j:=j+1 end;
i:=i+1
End;
for i:=1 to k do if mr[i].tb>0 then writeln(mr[i].tb:3,mr[i].ch:4); writeln; {вывод объединенного массива Работ}
{------------------считывание тарифов в массив Tar-----------------------------------}
assign(t,'tarif'); reset(t);
m:=0; {количество строк тарифов}
while not eof(t) do begin m:=m+1; read(t,mt[m]) end;
for i:=1 to k do writeln(mt[i].tb:3,mt[i].im:6,mt[i].tr:5); writeln;
Close(t);
{------------------расчет ведомости на оплату-------------------------------------------}
assign(v,'ved'); rewrite(v);
sch:=0;szr:=0;snl:=0;zvd:=0; {суммы}
for i:=1 to k do begin
if mr[i].tb=0 then continue; {если номер пуст - пропуск}
mv.tb:=mr[i].tb; mv.ch:=mr[i].ch;
for j:=1 to m do begin {поиск табеля в массиве MT}
if mv.tb=mt[j].tb then begin {расчет}
mv.im:=mt[j].im; mv.zr:=mv.ch*mt[j].tr;
mv.nl:=mv.zr*0.13; mv.vd:=mv.zr-mv.nl;
sch:=sch+mv.ch; szr:=szr+mv.zr;
snl:=snl+mv.nl; zvd:=zvd+mv.vd;
writeln(mv.tb:2,mv.im:5,mv.ch:4,mv.zr:5,mv.nl:5:0,mv.vd:5:0);
write(v,mv); {занесение записи в ведомость Ved}
Continue
End;
end; {for j}
end; {for i}
mv.tb:=0; mv.im:='Итог'; mv.ch:=sch; mv.zr:=szr; mv.nl:=snl; mv.vd:=zvd;
write(v,mv); {занесение итоговой записи в ведомость Ved}
{-------------------------------печать ведомости-------------------------------------------}
Reset(v);
writeln(' Платежная ведомость');
writeln('Таб Имя Дни Зарп Налог Выдать');
While not eof(v) do begin
Read(v,mv);
writeln(mv.tb:3,mv.im:5,mv.ch:4,mv.zr:6,mv.nl:7:1,mv.vd:7:1);
End;
End.
Замечание. Предложенное решение имеет недостаток. Хотя данные и хранятся в файлах, обрабатываются они в массивах. Т.е., если объем данных велик и они не могут быть размещены в основной памяти (в виду ограниченности ее размера), этот метод непригоден. На практике, возможно, придется обрабатывать данные непосредственно в файлах.
В приведенной программе для наглядности предусмотрен вывод всех промежуточных данных.
@ Задание 9.1. Составить программу вычисления суммы S(3х2) двух произвольных матриц А(3х2) и В(3х2) и записи матрицы S в файл sum типа Integer. Составить программу чтения и вывода из файла этой информации.
ПОДПРОГРАММЫ
Подпрограммы дают возможность делать приложения более компактными, позволяя для повторяющихся процессов писать код только один раз. Различают два вида подпрограмм: процедуры и функции.
üPROCEDURE имя_процедуры (список_параметров)
üFUNCTION имя_функции (список_параметров): тип_результата
Внутрь подпрограмм через список параметров передаются переменные для обработки. Для каждой из них указывается тип. Функция отличается от процедуры тем, что результат передается через ее имя. Ниже приведены примеры процедуры и функции, выполняющие одну и ту же операцию суммирования.
procedure Sum(x,y,s:real); function Sum(x,y:real):real;
begin begin
s:=x+y sum:=x+y
end; end;
Для обращения к процедуре нужно использовать оператор вида sum(a,b,c). Здесь переменные a,b,c называются фактическими параметрами, x,y,z – формальными. При исполнении процедуры значения a,b присваиваются переменным x,y и выполняются вычисления. Их результат через переменную с передается в вызывающую процедуру. К функции можно обращаться, используя оператор вида c:=sum(a,b).
@ Задание 10.1. Вычислить N элементов ряда:
y=x11!/2!–x32!/3!+x43!/4!–x54!/5!+... для Х<1 в двух вариантах:
При вычислении факториала использовать: 1). процедуру, 2). функцию.
ГРАФИКА
Графический режим ПК зависят от типа монитора и видиоадаптера. Мы будем использовать лучший доступный в Паскале режим: VGA, максимальное разрешение 640х480 точек (пикселей), 16 цветов. Соответствующий драйвер находится в файле EgaVga.bgi. Графический режим определяет команда
InitGraph(драйвер, мода, путь к файлу драйвера)
здесь: драйвер – номер драйвера (для VGA это 9), мода – номер режима (для 640х480 это 2), путь к файлу драйвера на диске.
Если файл находится в директории Паскаля, путь можно не указывать, а ввести пустые кавычки. Параметры драйвера и моду можно не задавать. Тогда они будут определены автоматически.
Возврат в текстовый режим экрана осуществляется оператором:
CloseGraph.
Паскаль располагает функциями, позволяющими осуществлять элементарные графические построения:
| GetMaxY | Вертикальный размер экрана по оси Y (в режиме VGA =479, поскольку отсчет точек от 0). |
| GetMaxX | Горизонтальный размер экрана по оси Х (в режиме VGA =639, поскольку отсчет от 0). |
| MoveTo(x,y) | Переместит курсор в позицию x,y. |
| MoveRel(dx,dy) | Переместит курсор от текущей точки на расстояние dx,dy |
| ClearDevice | Очищает экран. |
| PutPixel(x,y,цвет) | Выводит заданным цветом точку в координатах x,y. |
| Line(x1,y1,x2,y2) | Проводит прямую от точки с координатами x1,y1 до x2,y2. |
| LineTo(x,y) | Проводит прямую от текущей точки до точки с координатами x,y. |
| LineRel(dx,dy) | Проводит прямую от текущей точки на расстояние dx,dy. |
| Rectangle(x1,y1, x2,y2) | Строит контур прямоугольника с координатами левого верхнего (x1,y1) и правого нижнего (x2,y2) углов. |
| Bar(x1,y1,x2,y2) | Закрашивает прямоугольную область с координатами левого верхнего (x1,y1) и правого нижнего (x2,y2) углов, установленным командой SetFillStyle, цветом. |
| Cyrcle(x,y,r) | Строит круг с центром в точке x,y и радиусом r. |
| Ellipse(x,y,угол1, угол2,Rx,Ry) | Строит эллиптическую дугу с центром в точке x,y от начального угла1 (в градусах) до угла2. Rx и Ry задают горизонтальный и вертикальный радиусы эллипса. |
| PieSlice(x,y, угол1, угол2,r) | Строит сектор круга с центров в точке х,у радиусом r от угла1 (в целых градусах) до угла2. Заполнение и закрашивание секторов осуществляется функцией SetFillStyle. |
| SetFillStyle( заполнение, цвет) | Определяет тип заполнения (0 нет, 1 сплошное, 2 горизонтальное, 3 штриховка /, 4 толстая штриховка /, 5 толстая штриховка \, 6 штриховка \, 7 +, 8 x, 9 клетка, 10 точки, 11 частые точки) и цвет заполнения фигур. |
| SetColor(цвет) | Устанавливает текущий цвет линий и символов: Black – 0, Blue – 1, Green – 2, Cyan – 3, Red – 4, Magenta – 5, Brown – 6, LightGray – 7, DarkGray – 8, LightBlue – 9, LightGreen – 10, LightCyan – 11, LightRed – 12, LightMagenta – 13, Yellow – 14, White – 15. |
| SetBkColor(цвет) | Устанавливает текущий цвет фона. |
| SetLineStile(тип, вид, толщина) | Устанавливает стиль линий. Тип: 0 – сплошная линия, 1– точечная, 2 – штрих-пунктир, 3 – пунктир. Вид: 0. Толщина: 1 или 3 пикселя. |
 Пример 11-1. Нарисовать на экране: 1). Две диагонали, пересекающиеся в центре. 2) Четыре концентрических окружности с центрами в центре экрана и радиусами 50, 100, 150, 200. Отсчет экранных координат начинается с левого верхнего угла: Х – вправо, Y – вниз.
Пример 11-1. Нарисовать на экране: 1). Две диагонали, пересекающиеся в центре. 2) Четыре концентрических окружности с центрами в центре экрана и радиусами 50, 100, 150, 200. Отсчет экранных координат начинается с левого верхнего угла: Х – вправо, Y – вниз.
Program P11_1
Uses graph;
var d,i,m,rx,ry:integer;
Begin
initgraph(d,m,''); {переход в графику}
ry:=getmaxy; rx:=getmaxx; {размер экрана}
line(0,0,rx,ry); {первая диагональ}
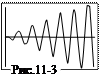 line(0,ry,rx,0); {вторая диагональ}
line(0,ry,rx,0); {вторая диагональ}
for i:=1 to 4 do begin {окружности}
circle(rx div 2,ry div 2,50*i);
End;
readln; {пауза для просмотра результата}
closegraph; {закрытие графического режима}
End.
Пример 11-2. Вывести на кран функцию f(x)=sin(x)×x вместе с координатными осями. Аргумент Х изменяется от начального значения Xn=0 до конечного Xk=20 с шагом dx=0.01. Главная проблема заключается в масштабировании исходной “натуральной” функции F в ее экранный вид Fэ: F(X)ðFэ(Xэ). Здесь следует учесть, что экранные координаты расположены (рис. 11.2) не так как мы привыкли. Точка 0э,0э находится в его верхнем левом углу (а не в центре), ось Yэ идет вниз (а не вверх), ось Xэ – идет вправо. Т.о. для адекватного отображения графика на экране нам понадобится реализовать три действия:
1. Масштабировать диапазоны D изменения натуральных Х и Y к желаемым экранным, т.е. привести DХ и DY к DХэ и DYэ соответственно с помощью масштабных коэффициентов Mx=DХэ/Dx и My=DYэ/DY.
2. Перенести координаты так, чтобы максимум Yэ приходился на верхнюю границу экранной области, а начальное значение X – на левую ее границу.
3. Перевернуть направление графика. Поскольку направление экранной оси ординат противоположно натуральному, знак изменения Yэ должен быть противоположен знаку Y.
Программа имеет следующую структуру. 1). Описывается функция вычисления f(x). 2). Выясняются размеры экрана, параметры аргумента, проводится вертикальная координата. 3).Находятся максимальные значения Y. 4). Выполняется масштабирование переменных (msy и msx). Эти значения указывают, сколько пикселей приходится на единицу изменения Y и Х соответственно. 5). Выполняется собственно рисование кривой. Здесь оно выполнено двумя способами – точками и отрезками линий. Проверьте результат в обоих случаях, поочередно убрав одну из них. 6). Проводится ось Х.
Program P11_2;
Uses graph;
var d,m,rx,ry:integer;
x,y,xn,xk,ymin,ymax,dx:real; msy,msx:real;
function f(x:real):real; {вычисление функции}
begin f:=sin(x)*x end;
Begin
initgraph(d,m,''); {переход в графический режим}
ry:=getmaxy+1; rx:=getmaxx+1; {размер экрана}
line(0,0,0,ry); {ось Y}
xn:=0; xk:=60; dx:=0.01;{параметры аргумента}
x:=xn; {начальное Х}
ymin:=f(x); ymax:=f(x);
while x<=xk do begin {поиск максимума и минимума Y}
y:=f(x);
if y>ymax then ymax:=y;
if y<ymin then ymin:=y;
x:=x+dx; {изменяем Х}
End;
msy:=ry/abs(ymax-ymin); {масштаб по Y}
msx:=rx/abs(xk-xn); {масштаб по X}
x:=xn; {начальное Х}
while x<=xk do begin {рисование}
y:=f(x);
putpixel(round((x-xn)*msx),-round((y-ymax)*msy),2); {точки}
lineto(round((x-xn)*msx),-round((y-ymax)*msy)); {отрезки}
x:=x+dx; {изменяем Х}
End;
line(0,-round(-ymax*msy),rx,-round(-ymax*msy)); {ось Х}
readln; {пауза для просмотра картинки}
Closegraph;
End.
 @ Здания для самостоятельного решения
@ Здания для самостоятельного решения
а). Решить аналогичную задачу, но ось Y направить горизонтально, а Х – вертикально.
б). Известна зарплата (массив z[1..5]) работников (N=5) бригады. Построить диаграмму из вертикальных линий.
в). Условие то же, но диаграмма столбиковая. Замечание. Ширина столбца определяется делением ширины экрана на число рабочих. Однако, если ширина столбца не кратна размеру экрана, крайний столбец будет отображен не полностью. При программировании следует учесть этот фактор, уменьшив ширину столбца.
г). Известна зарплата (массив z[1..5]) и премия (массив p[1..5]) каждого из N=5 работников бригады. Построить совмещенную столбиковую диаграмму (на столбике зарплаты стоит столбик премии). Премия должна быть заштрихована командой SetFillStyle.
д). Для той же задачи построить секторную диаграмму зарплат. Указание. Сначала следует найти сумму всех зарплат s. Затем перевести зарплату каждого работника в градусы его сектора на диаграмме z[i]/s*360 и запомнить ее в массиве z[1..5]. Далее вычислить начальный и конечный угол каждого радиуса каждого сектора, нарисовать диаграмму командой PieSlice и раскрасить ее.
Литература. При изучении предмета можно использовать любую доступную книгу, содержащую сведения по языку Паскаль. В библиотеке МГУТУ имеется учебное пособие: Попов А.А. Программирование и основы алгоритмизации, Программирование на языках высокого уровня. – М., МГУТУ, 2004.
Задание на курсовую работу
Оформление работы. Работа должна содержать формулировку задания, краткие объяснения по ее решению, математические выкладки (если необходимы) и подробно прокомментированный текст программы. Работа должна быть написана (или напечатана) на листах формата А4 (на гладких или в клетку) и помещена в пластиковый скоросшиватель. Каждый оператор программы должен быть размещен на отдельной строке. На титульном листе студенту следует указать свои обычные реквизиты.
Задание. Вариант определяется числом, образованным двумя последними цифрами шифра студента, следующим образом. Если это число меньше 33, из перечня вариантов берется вариант с идентичным номером, если более, то из числа, взятого из шифра вычитается 33 до тех пор, пока не останется число £32. Например, для шифра 26 необходимо выполнить 26-ой вариант, для шифра 50 вариант вычисляется как 50-33=17 (т.е. 17-тыи вариант), для 94 это 94-66=28.
В курсовой работе требуется составить программу, выполняющую указанные в варианте преобразования с квадратной А(N,N) матрицей. При этом следует нарисовать исходную матрицу с индексами ее элементов и преобразованную с новым содержимым (аналогично рисункам к примеру 6.4). Если в условии задачи речь идет о перемещении элементов матрицы, то в качестве исходных данных лучше брать не произвольные числа, а индексы этих элементов (например содержимым клетки А(2,5) лучше взять число 25). Тогда легче разработать алгоритм программы, написать ее и отладить. Программа должна строиться таким образом, чтобы существовала возможность ее использования с массивами любой размерности, содержащими произвольные элементы. В программе должна быть предусмотрена выдача на печать исходных и преобразованных матриц и других, указанных в задании, результатов вычислений. Если решение задачи критично к факту четности/нечетности числа столбцов или строк, студент сам выбирает этот параметр. Ниже для пояснения сути задания ниже некоторые варианты сопровождаются рисунками.
Полученные результаты должны быть занесены в последовательный файл и доступны для просмотра из него.
0. В матрице А(N,N) найти элементы, встречающиеся более одного раза. Из этих элементов составить и напечатать матрицу Х из двух столбцов. В первом столбце разместить сами значения таких элементов, во втором – количество раз, которое они встретились. Составить и напечатать новую матрицу B(N,N), элементами которой являются числа, указывающие сколько раз встретился элемент, находящийся в этой же позиции в А(N,N).
1. В матрице А(N,N) найти элементы, встречающиеся не более одного раза. Напечатать их значения, индексы и сумму S, а также исходную матрицу, где отображены только эти элементы (остальные элементы при печати замещаются значком “–“).
2. В матрице А(N,N) найти элемент, который является одновременно максимальным в строке и минимальным в столбце. Если такого элемента нет, должно быть выдано сообщение “элемент не найден”. Если такой элемент имеется, вычислить суммы S1, S2, S3, S4 чисел, находящихся в четвертях, отсекаемых найденными столбцом и строкой.
3. В матрице А(N,N) найти максимальный МХ и минимальный MN элементы, а также произведение P всех элементов, находящемся в прямоугольнике минимальных размеров, включающий оба этих элемента и сумму S элементов, находящихся вне этого прямоугольника. Замечание: в случае, если оба элемента находятся в одной строке/столбце, прямоугольник превращается в фрагмент этой строки/столбца.
4. В матрице А(N,N) все ее элементы повернуть на четверть по часовой стрелке и разместить их в матрице X(N,N). На рисунке к варианту слева показан исходный, а справа – преобразованный виды матрицы.
5. В матрице А(N,N) все ее элементы повернуть на четверть против часовой стрелки и разместить их в матрице X(N,N). На рисунке к варианту слева показан исходный, а справа – преобразованный вид матрицы.
6÷12. В матрице А(N,N) уплотнить все четные элементы в направлении указанном на рисунке. Остальные элементы сделать равными нулю.
13÷20. Заполнить матрицу А(N,N) числами натурального ряда в последовательности, указанной на рисунке и найти их сумму.
21÷28. В матрице А(N,N) уплотнить все нечетные элементы в направлении указанном на рисунке. Остальные элементы сделать равными нулю.
29÷32. Расположить в матрице А(N,N) элементы в порядке их убывания в последовательности, указанной на рисунке.
 | ||
 |
 | ||||
 | ||||
 |







