Содержание
Рабочая программа........................................................ 3
Программирование на Паскале.................................. 4
Введение...................................................................... 4
Простейшие операторы языка.............................. 5
Организация ветвлений........................................... 8
Логические функции.............................................. 10
Организация циклов............................................... 12
Массивы.................................................................... 19
Символьные данные.............................................. 25
Записи........................................................................ 29
Файлы........................................................................ 29
Графика..................................................................... 36
Литература..................................................................... 40
Задания на курсовую работу.................................... 40
РАБОЧАЯ ПРОГРАММА
Целью дисциплин Алгоритмизация и основы программирования, Программирование на языках высокого уровня является углубление навыков по технике программирования на ЭВМ.
ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ
Цель преподавания дисциплин является углубление навыков по технике программирования на ЭВМ.
Задачи изучения дисциплины. Студент должен:
ИМЕТЬ ПРЕДСТАВЛЕНИЕ: о современных алгоритмических языках.
ЗНАТЬ: Инструментальные средства языка Паскаль.
УМЕТЬ: Программировать на алгоритмическом языке Паскаль, включая постановку задачи, разработку алгоритма, составление программы, ее отладку и интерпретацию результатов счета.
ПРИОБРЕСТИ НАВЫКИ: самостоятельной работы на компьютере.
ТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ ПРОГРАММЫ
1. Алфавит языка. Константы и переменные. Типы данных.
2. Операторы ввода-вывода. Оператор присваивания. Основные функции.
3. Операторы анализа условий. Логические функции. Задачи с ветвлениями.
4. Построение циклов, их типы. Операторы циклов. Задачи на накопление.
5. Работа с массивами.
6. Символьные функции. Работа со строками.
7. Использование процедур.
9. Графические средства языка.
9. Записи. Работа с файлами.
ПЕРЕЧЕНЬ РЕКОМЕНДУЕМЫХ ЛАБОРАТОРНЫХ РАБОТ
1. Программирование алгоритмов с ветвлениями.
2. Программирование циклов. Числовые и функциональные ряды.
3. Работа с одномерными и двумерными массивами.
4. Работа с символьными данными.
5. Работа с графикой
6. Работа с файлами
Лабораторные работы приведены в данной методичке под заголовком “Задания для самостоятельного решения” (@).
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО ДИСЦИПЛИНЕ
На экзамен выносится один теоретический вопрос из следующего списка и задача для решения на компьютере.
Программирование процессов. Этапы решения задач на ЭВМ. Типы алгоритмических языков. Особенности изучаемого языка. Оператор присваивания. Оператор ввода. Операторы вывода. Форматирование вывода. Операторы перехода. Ветвящиеся программы. Итерационные циклы. Арифметические циклы. Оператор цикла. Работа с массивами. Методы сортировок. Организация процедур. Графические операторы. Погрешности при цифровых вычислениях.
Программирование на алгоритмическом
языке Паскаль
1. ВВЕДЕНИЕ
Алгоритмические языки предоставляют возможность человеку управлять действиями ЭВМ. Существует несколько таких языков, среди которых очень популярным является Турбо Паскаль (далее просто Паскаль).
Символы. В Паскале разрешены следующие основные символы: 1. Буквы латинского и русского языков (кириллица используется только в константах). 2. Цифры. 3. Символы: + – * / = > <., () [ ] ‘; ^: и другие.
Операции. Арифметические: +, –, * (умножение), / (вещественное деление). Операции отношений: =, >, <, >= (больше или равно), <= (меньше или равно), <> (не равно). Операции возведения в произвольную степень в Паскале нет. Кроме перечисленных, имеются еще две арифметические операции над целыми числами:
div – целочисленное деление (дробь отбрасывается, например 14 div 3=4),
mod – целочисленный остаток от деления (пример 14 mod 3=2),
Переменные снабжаются именами, которые могут содержать латинские буквы, цифры и знаки подчеркивания, но начинаться имя должно с буквы. Программист выбирает имена произвольно, но таким образом, чтобы они указывали на смысл переменной. За каждой переменной компьютер закрепляет одну ячейку памяти. Большие и маленькие буквы в именах воспринимаются компьютером одинаково, т.е. буквы W и w обозначают одну и ту же переменную. Примеры имен: Х, y, A24, VES_Netto, MAXIMUM.
Типы переменных. Всем переменным в программе предварительно должны быть указаны типы. Вот важнейшие.
числовой целый Integer (диапазон от –32768 до +32767)
числовой целый длинный Longint (от –2147483648 до +2147483647)
числовой вещественный Real (от 2,9Е-39 до 1,7Е+38)
символ Char (один символ)
строка символов String (до 255 символов)
логический Boolean (значения: true – истина, false – ложь).
Задание типа производится оператором VAR. Например:
VAR a,d: INTEGER; x: REAL; d: STRING;.
В разделе констант можно сразу задать и тип и значение переменной
CONST b: INTEGER=5; s:STRING=’поле’.
Здесь переменным придаются и типы и значения.
Выражения используются для отображения формул и записываются в строку. Вычисления в них реализуются слева направо в общепринятой последовательности: 1. вычисление функций, 2. умножение-деление, 3. сложение-вычитание. Порядок действий может быть изменен скобками. Следующий пример иллюстрируют правила построения выражений (слева в рамке формула в обычной записи, справа выражение на Паскале):
 è A/(3*B)+X/(Y+1)*4
è A/(3*B)+X/(Y+1)*4
Функции реализуют стандартные действия. Функции всегда содержат скобки (кроме Pi). Ниже показаны важнейшие:
| Функция | Назначение | Тип аргумента | Тип результата | Примеры |
| abs(x) | модуль х | целый/ веществ. | как у аргумента | abs(–6)=6 |
| sin(x) | синус угла х | веществ. в радианах | веществ. | |
| cos(x) | косинус угла х | |||
| arctan(x) | арктангенс х | |||
| sqrt(x) | квадратный корень из х (х≥0) | целый/ веществ. | как у аргумента | |
| sqr(x) | квадрат х | |||
| exp(x) | ex | веществ. | веществ. | |
| ln(x) | логарифм натуральный х (x>0) | |||
| int(x) | целая часть числа х | int(1.2)= int(1.9)=1 | ||
| frac(x) | дробная часть числа х | frac(2.5)=0.5 | ||
| odd(x) | выявление нечетности х | целый | логический | odd(3)=true |
| pi | число π=3.14159... | веществ. | ||
| trunc(x) | отбрасывает дробную часть х | веществ. | целый | trunc(3.7)=3 |
| round(x) | округляет вещественное х до целого | веществ. | целый | round(3.7)=4 |
Преобразование вещественного типа в целый осуществляется функциями round и trunc. Преобразование в вещественный тип может быть осуществлено простым присваиванием вида
вещественная переменная:=целочисленная переменная
(например a:=d). Такое преобразование называется неявным.
2. ПРОСТЕЙШИЕ ОПЕРАТОРЫ ЯЗЫКА
Оператор – основная единица программы и имеет множество разновидностей. Рассмотрим пока самые простые.
Оператор присваивания. Общий вид оператора присваивания:
üпеременная:=выражение
Такая запись означает, что выражение, стоящее справа, вычисляется и его результат присваивается переменной, стоящей слева. Примеры операторов: Z:=2, А:=3.5+exp(8), S:=X*4+Y/2.
Присваивание не является равенством в обычном смысле. Здесь справа и слева от знака равно можно указывать одну и туже переменную. Например, допустимо: М:=М+2, X:=X/3. Эти выражения следует понимать так, что новое содержимое ячейки М будет равно старому, увеличенному на два, и новое Х будет равно старому, деленному на три. Например, если ранее было М=3 и Х=12, то после вычислений получим М=3+2=5 и Х=12/3=4.
Оператор вывода. Для анализа результатов вычислений необходимо вывести их на внешний носитель – бумагу или экран дисплея. Для этой цели используется оператор.
üWRITE(список_выводимых _ переменных)
üWRITELN(список_выводимых _ переменных)
Так оператор WRITELN(a,m) читается – “Печатать переменные А, М”.
Различие двух форм оператора заключается в том, что вторая разновидность после вывода данных переводит курсор на новую строку (line). Оператор writeln может использоваться и без аргументов (и без скобок). Тогда при выводе будет формироваться только пустая строка. В оператор могут включаться не только переменные, но и константы и выражения. Например, если Х=12, а Y=100, то применение оператора WRITE('X=', x, ' Y=', y, ' СУММА=', x+y) даст такой результат: X=12 Y=100 СУММА=112.
С помощью оператора можно указать не только что будет выведено, но и как, т.е. отформатировать вывод. После имени вещественной переменной можно (через двоеточие) задать два числа. Первое из них задаст общую длину вывода числа, второе – размер дробной части. После имени целочисленной переменной нужно задать только одно число. Например, оператор WRITE(k:6,z:8:2) при выводе отведет для целочисленной переменной K 6 позиций, а для вещественной переменной Z – 8, из которых 2 под дробную часть. Лишние позиции, отведенные под целую часть, заместятся пробелами.
Оператор ввода. Исходные данные, обрабатываемые программой, должны вводиться пользователем с помощью оператора чтения данных:
üREADLN(список_вводимых_переменных)
Встречая такой оператор, компьютер останавливается и ждет вашего ввода. Число вводимых данных по количеству и типу должно соответствовать списку переменных. Если список содержит более одной переменной, действия пользователя зависят от типов, вводимых данных. Числовые значения разделяются нажатием Enter или пробелом, а в конце Enter. Если вводятся данные типа char – символы набирать следует подряд. Данные типа string разделяются пробелом. Оператор может и не иметь аргументов вовсе (readln()). Тогда все, что вы можете сделать, это нажать Enter.
Пример: READLN(r,l). Дословно, оператор интерпретируется так: “Читать в память компьютера, введенные с клавиатуры, переменные R и L”. Пусть в нашей программе R=5 и L=8.4. Тогда пользователь должен ввести 5 и 8.4 через пробел или Enter.
С тем, чтобы пользователь понимал, чего от него хочет компьютер, а не видел лишь черный экран с курсором, удобно прежде оператора ввода разместить оператор вывода с необходимым текстом-подсказкой.
üEXIT – Оператор завершения используется для принудительного завершения программы/процедуры в любом ее месте.
üREADKEY – Оператор ожидания нажатия клавиши может использоваться для создания паузы в программе, например, для того, чтобы разглядеть, что выведено на экране.
üCLRSCR – Оператор очистки освобождает экран и устанавливает курсор в левый верхний угол.
Этот оператор и оператор readkey находятся в библиотеке CRT Паскаля и, чтобы ими воспользоваться, следует ее подключить оператором USES CRT.
üКомментарии. Для того чтобы не забыть, зачем введен тот или иной оператор, программы снабжаются текстовыми комментариями. Они могут занимать целые строки или быть записаны непосредственно справа от комментируемого оператора. Комментарии ограничиваются фигурными скобками и никак не влияют на вычисления.
Операторные скобки используются, чтобы выделить некоторую группу операторов как единое целое.
üBEGIN...END
и особенно необходимы в конструкциях, которые будут рассмотрены позже, но в каждой программе они используются для указания начала и завершения рабочей части программы. При этом слово end замыкается точкой.
Запись операторов. Оператор может занимать любое количество строк и для переноса на другую строку не нужно никаких символов переноса. Все операторы Паскаля завершаются знаком “точка с запятой”. Однако после оператора begin и перед оператором end точку с запятой можно не ставить.
Структура программы на Паскале имеет две части: описательную (пункты 1,2,3) и вычислительную и состоит из следующих элементов (рис. 2.1):
1. Задается имя программы (необязательно).
2. Присоединяются нужные модули и библиотеки Паскаля (необязательно).
3. Описываются все участвующие метки, переменные, константы, типы и др.
4. Оператором Begin открывается вычислительная часть.
5. Внутри блока помещаются операторы собственно программы.
 6. Оператором End (с точкой) завершается вся программа.
6. Оператором End (с точкой) завершается вся программа.
Теперь напишем простую программу (рис. 2.2) вычисления площади круга S произвольного радиуса R по известной формуле S=πR2. Программу назовем KRUG. Переменные S и R обозначим как вещественные, поскольку они могут иметь дробную часть. Ввод радиуса осуществляется оператором readln(r). Чтобы пользователь понимал, что именно он должен ввести, прежде оператором write(‘радиус=’) на экран выводится слово “радиус=”. В конце программы видим оператор readkey. Он нужен для удобства отладки. Встречая его, компьютер ожидает от пользователя нажатия любой клавиши. В это время он может без спешки осмотреть результаты счета. Если этого не сделать Паскаль сразу же вернет нас в окно редактирования и тогда окно выдачи придется вызывать клавишами Alt+F5, что неудобно. Остальное очевидно.
Замечание. В текстах следующих примеров для компактности мы не будем использовать операторы очистки экрана, задержки readkey и, в большинстве случаев, операторы-подсказки ввода, однако студент должен это делать.
ОРГАНИЗАЦИЯ ВЕТВЛЕНИЙ
Программа, которую мы разобрали, называется линейной поскольку все операторы выполнялись один за другим в порядке их записи. На практике это редкий случай. Чаще бывает, что такой порядок должен быть нарушен. Для этого используются следующие операторы.
Условный оператор позволяет выполнять некоторые действия в зависимости от заданных условий.
üIF логическоеусловие THEN оператор1 ELSE оператор2
 Здесь, если условие истинно, выполняется оператор1, иначе оператор2. Например, оператор
Здесь, если условие истинно, выполняется оператор1, иначе оператор2. Например, оператор
IF a>b THEN WRITELN ('А больше В') ELSE WRITELN ('А не больше В');
выводит словесное сообщение о соотношении переменных А и В.
Оператор может использоваться и в усеченной форме без опции ELSE.
Другой пример. На практике иногда приходится выяснять кратность числа (например Х) некоторому другому числу (Y). Это можно сделать с помощью следующего выражения (оба числа должны быть целого типа)
IF x MOD y =0 THEN WRITELN ('X кратно Y')
ELSE WRITELN ('X не кратно Y')
Всюду, где в синтаксисе команд встречается слово “оператор”, может быть записано любое число операторов, заключенных в операторные скобки BEGIN...END.
Пример. Напишем оператор взятия корня числа х с учетом его знака.
IF x>0
THEN BEGIN y:=SQRT(x); WRITELN('корень=', y) END
ELSE WRITELN('число отрицательно')
За мечание. С целью придания наглядности подчиненные (вложенные) операторы удобно вводить с некоторым отступом, как показано выше.
 Внутрь оператора if могут быть вложены другие if. Например, пусть в последовательности чисел a,b,c требуется вывести первое по порядку положительное число. Если таковых не оказалось, печатать “Все числа меньше 0”. Программа справа.
Внутрь оператора if могут быть вложены другие if. Например, пусть в последовательности чисел a,b,c требуется вывести первое по порядку положительное число. Если таковых не оказалось, печатать “Все числа меньше 0”. Программа справа.
 Оператор безусловного перехода. Оператор вида:
Оператор безусловного перехода. Оператор вида:
üGOTO меткаоператора
вынуждает программу выполнять не следующий по порядку оператор, а оператор с указанной меткой. Например, оператор GOTO m читается как “Идти к оператору с меткой m” и передает ему управление. Метки должны быть предварительно объявлены оператором label в разделе объявлений программы (в нашем случае label m). Меткам можно давать произвольные символьные или числовые имена, важно чтобы все метки были разными, т.е. никогда не совпадали в пределах программы. В операторе, на который происходит ссылка, метка ставится перед ним и отделяется двоеточием.
Очень распространенной задачей является программирование алгоритмов с несколькими исходами – ветвящихся процессов. Здесь удобно (по крайней мере, на первом этапе) сначала построить блок-схему, дающую наглядное графическое представление алгоритма. В блок-схеме отдельные операции или их группы помещаются в прямоугольные блоки. Операции анализа отображаются ромбами. Обозначение других операций будет рассмотрено позже. Блок-схемы обрамляют блоки НАЧАЛО и КОНЕЦ. Мы будем изображать последние только в случае, если возможно разночтение.
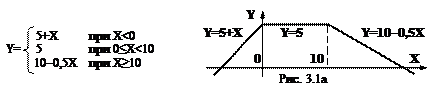 Пример 3-1. Для произвольного аргумента Х вычислить значение кусочно-ломаной функции Y(X) (рис. 3.1а).
Пример 3-1. Для произвольного аргумента Х вычислить значение кусочно-ломаной функции Y(X) (рис. 3.1а).
Отметим, что практически любая задача может быть запрограммирована по-разному. Два таких решения приведены в program p3_1 (рис. 3.1б и 3.1в). Второй вариант работает быстрее поскольку, если обнаружено выполняющееся условие, следующие условия не проверяются.
 |
Пример 3-2. Даны три произвольных числа А, В, С. Составить программу, которая анализирует их и, если сумма первых двух чисел не меньше третьего, а второе больше первого – выдает сообщение ВЕРНО. Если хотя бы одно из условий не выполняется, – то сообщение НЕВЕРНО. Иными словами
 “ ВЕРНО ” если А+В>=C и В >A
“ ВЕРНО ” если А+В>=C и В >A
“ НЕВЕРНО ” – в противном случае
Несмотря на простое условие, программа (program P3_2) получилась достаточно запутанной. При необходимости выполнять анализ одновременно нескольких условий удобно пользоваться логическими функциями. Аргументами логических функций являются высказывания, которые могут быть либо истинными, либо ложными. К таким высказываниям относятся операции отношения (равно, больше, меньше и т.д.). Так, например, отношение вида Х=Y всегда может быть только истинным или только ложным.
ЛОГИЧЕСКИЕ ФУНКЦИИ
Функция одного аргумента НЕ (NOT) истинна тогда, когда ложен ее аргумент (значение функции обратно аргументу). Поведение функции полностью описывает таблица. Например, следующие два оператора идентичны
if x<10 then y=5 if not (x>=10) then y=5
Функций двух аргументов. Функция И (AND) истинна когда истинны все ее аргументы. Функция ИЛИ (OR) истинна, если истинен хотя бы один из аргументов. Если нет скобок, функции вычисляются в следующей последовательности: НЕ, И, ИЛИ. Значениям Истина и Ложь в Паскале соответствуют значения True и False.
| аргу- мент | функция НЕ | 1-й аргумент | 2-й аргумент | функция И | функция ИЛИ | |
| ложь | истина | ложь | ложь | ложь | ложь | |
| истина | ложь | ложь | истина | ложь | истина | |
| истина | ложь | ложь | истина | |||
| истина | истина | истина | истина |
Логические операции имеют приоритет перед операциями отношения, поэтому, если таких условий несколько, последние берутся в скобки. Для иллюстрации снова рассмотрим пример 3-2. Решение будет очень компактным (вспомогательные операторы опущены):
Readln(a,b,c);
if (a+b>=c) and (b>a) then writeln('верно') else writeln('неверно');
Пример. Для чисел А, В, С выяснить, правда ли что первое число самое большое, а последнее – самое маленькое.
if (a>b) and (a>c) and (c<a) and (c<b)
then writeln('верно') else writeln('неверно');
Еще. Верно ли, что среди чисел есть отрицательные.
if (a<0) or (b<0) or (c<0) then...
Еще. Верно ли, что среди чисел ровно одно меньше нуля.
if (a<0)and(b>0)and(c>0) or (a>0)and(b<0)and(c>0) or (a>0)and(b>0)and(c<0)
then writeln('верно') else writeln('неверно');
В этом решении перебираются все возможные, интересующие нас, комбинации переменных. Иногда проще (см. справа) воспользоваться косвенным способом, например, увеличивать вспомогательную переменную Х, каждый раз, когда встречается число меньше нуля. Если в конце окажется, что Х=1 значит, имеется ровно одно число меньшее нуля.

 Оператор выбора (селектор). При необходимости сделать выбор из многих альтернатив конструкция с вложением if становится очень громоздкой. В этом случае полезным оказывается оператор case. Здесь выражение может быть целого или символьного типа. Если его значение равно одной из констант, выполняется соответствующий оператор. Если ни одна из констант не подходит, выполняется оператор, следующий после слова else (если есть). Любая из констант может быть диапазоном (через две точки) и/или множеством констант (через запятую). Любой оператор может быть блоком begin и содержать свои операторы case и if.
Оператор выбора (селектор). При необходимости сделать выбор из многих альтернатив конструкция с вложением if становится очень громоздкой. В этом случае полезным оказывается оператор case. Здесь выражение может быть целого или символьного типа. Если его значение равно одной из констант, выполняется соответствующий оператор. Если ни одна из констант не подходит, выполняется оператор, следующий после слова else (если есть). Любая из констант может быть диапазоном (через две точки) и/или множеством констант (через запятую). Любой оператор может быть блоком begin и содержать свои операторы case и if.
Пример 4-1. Пусть требуется по числу прожитых лет Т отнести человека к какой-то возрастной группе. Решение очевидно, но нуждается в одном пояснении. Поскольку женщины и мужчины уходят на пенсию в разное время (55 и 60 лет), кроме возраста нужно учитывать и пол Р.
 |
Пример 4-2. Положим, введен какой-то знак в переменную S и его нужно отнести к соответствующей группе. Следует сказать, что латинские символы в символьной таблице ПК находятся не вместе. Подряд идут буквы с А по Z, затем идут не буквы, затем буквы с а по z. В виду этого пришлось указать два диапазона констант ('A'..'Z','a'..'z'). Символы русского алфавита состоят из еще большего числа диапазонов (см. раздел ‘Символьные данные’).
@ Здания для самостоятельного решения
Задание 4.1. Имеются числа a, b, c. Выяснить, правда ли, что они расположены в порядке возрастания.
Задание 4.2. Выяснить, правда ли, что среди чисел a,b,c имеется хотя бы одно отрицательное и одно положительное (ответ Да/Нет)
Задание 4.3. Имеются числа a, b, c. Вывести их в порядке возрастания.
Задание 4.4. Выяснить, правда ли, что среди a,b,c имеется точно один 0.
 Задание 4.5. На рис. 4.1 изображены две пересекающиеся линии Y1=X2и Y2=1–X/2. По произвольным значениям координат некоторой точки X и Y найти область ,‚, ƒ,„, в которой находится эта точка. Ответ должен быть выдан в виде числа 1, 2, 3, 4. Если точка находится вне этих областей, ответом должно быть выражение – “Вне областей”.
Задание 4.5. На рис. 4.1 изображены две пересекающиеся линии Y1=X2и Y2=1–X/2. По произвольным значениям координат некоторой точки X и Y найти область ,‚, ƒ,„, в которой находится эта точка. Ответ должен быть выдан в виде числа 1, 2, 3, 4. Если точка находится вне этих областей, ответом должно быть выражение – “Вне областей”.
Сейчас определим только принадлежность точки к области 2. Сначала выясним диапазон изменения Х в области. Очевидно, он простирается от Х=0 до координаты Х, где пересекаются прямая и парабола (белая точка на рисунке). Чтобы ее найти, надо приравнять выражения для обеих функций X2=1–X/2 и, преобразовав его в квадратное уравнение 2X2+X–2=0, вычислить левый корень Х=–1,28. Отсюда можно записать –1,28<X<0. Для Y можно сказать, что он лежит под прямой Y<1-X/2 и над параболой Y>X2. Таким образом, должны выполняться условия –1,28<X<0 и Y<1–X/2 и Y>X2. Отсюда можно записать оператор IF:
IF (–1,28<X)and(X<0)and(Y<1–X/2)and(Y>X*X) then?”Это область 2”
Завершите решение для остальных областей.
Задание 4.6. Используя оператор CASE, написать программу, в которой вводятся два числа-операнда Х и Y и знак операции Z (+,–,/,*). Вычислить результат S в зависимости от знака. Предусмотреть реакции на возможный неверный знак операции, а также на ввод Y=0 при попытке выполнить деление ('Деление на ноль не возможно')
ОРГАНИЗАЦИЯ ЦИКЛОВ
В простых примерах, рассмотренных выше, вообще говоря, не требовалось привлечения программирования. Все они легко могли быть решены вручную или с помощью калькулятора. Сила ЭВМ заключается в возможности простыми средствами осуществлять многократное повторение заданных действий – циклов.
Итерационные циклы. В случае, если число циклов, необходимых для решения задачи, заранее неизвестно, такие циклы называются итерационными. Рассмотрим ряд примеров.
Пример 5-1. Пусть для некоторого множества чисел Х нужно вычислить и отпечатать функцию Х/2. Ввод и вычисления следует прекратить после обнаружения первого Х, равного нулю. Очевидна следующая блок-схема (рис. 5.1а). Блоков ввода, вычисления, печати и анализа столько, сколько чисел в последовательности до первого нуля. Чисел может быть очень много и подобный подход, конечно, неприемлем, не говоря уже о том, что заранее неизвестно, когда встретится ноль.
Такие программы строятся по-иному. Обрабатывающая часть цикла записывается только раз, но охватывается петлей возврата (рис. 5.1б). Тогда одни и те же операторы будут выполняться многократно до тех пор, пока Х¹0. Для реализации цикла здесь понадобилась метка (m).
 |
@ Задание 5.1. Наберите программу Р5_1. Затем улучшите ее: введите необходимые подсказки, отформатируйте вывод, сделайте очистку экрана, введите подсчет количества точек Х, для которых был вычислен Y. Выдайте сообщение “Х=0” по завершении программы.
Пример 5-2. Пусть для аргумента Х в диапазоне 3÷9, требуется вычислить значение функции Y=(X–6)2, где Х изменяется с шагом 2 (рис. 5.2а,б). Справа от текста программы сделаны выкладки по проверке решения. В каждой строке вручную вычисляется значение соответствующей переменной. Проверка выполняется сверху-вниз, слева-направо по ходу исполнения программы. Стрелки показывают связи между циклами. Видим, что заданная последовательность изменения Х (3,5,7,...) наблюдается и последнее Y вычисляется для Х=9. При следующем приращении Х оно становится равным 11 и пятый цикл не выполняется, поскольку Х>9. Программа завершается. Следует отметить, что нет никакого технически простого способа проверки правильности написанных программ. Для этой цели программисту приходится вручную по тексту программы рассчитывать значения переменных и сличать их с желаемыми (известными из условия). Конечно, проверка выполняется не для всей задачи, а только для небольшого числа (например, 3-х) начальных циклов и при этом тщательно анализируется значение условия выхода из цикла (здесь оператор IF).
 |
Задание 5.2. Вычислите функцию в обратном порядке. Подсчитайте среднее арифметическое всех Х и Y (SX и SY).
Арифметические циклы. Если число повторений известно заранее – такие циклы называются арифметическими.
Пример 5-3. Пусть в условиях предыдущего примера не известно предельное значение аргумента, но зато задано количество точек аргумента – 4. Поскольку в данном случае не задано последнее значение Х, признак окончания циклов придется формировать самим. Для этого вводится переменная, которая фиксирует число уже выполненных циклов – счетчик циклов (назовем ее I). В исходном состоянии (рис. 5.3) берем его равным 1. После выполнения очередного цикла счетчик получает приращение на единицу (I=I+1). В начале каждого цикла в операторе IF делается проверка на достижение счетчиком последнего разрешенного значения (у нас 4). Если I<=4 программа продолжает вычисление функции, если нет (I>4) – счет прекращается. Рядом с программой приведены выкладки по ее проверке. Как видим, результат проверки совпал с результатом, полученным ранее. Очевидным что счетчик циклов I должен быть целого типа.
 |
@ Задание 5.3. Напишите программу вычисления функции в обратном порядке. Сделайте число точек не константой (4), а переменной N, вводимой оператором read. При прогоне программы задайте N=100. Поскольку весь результат теперь не умещается на экране, организуйте паузу при выдаче каждых 20-ти строк (понадобится операция mod и readkey).
 program P5_3; program P5_3;
| проверка | ||||
| label d; var x,y:real; i:integer; begin | цикл | цикл | цикл | цикл | |
| x:=3; i:=1; d: if i>4 then exit; y:=sqr(x–6); writeln(x,y); x:=x+2; i:=i+1; goto d; end. | x=3, i=1
 i=1<4
y=9
3, 9
x=5
i=2 i=1<4
y=9
3, 9
x=5
i=2
|
 2<4
y=1
5, 1
x=7
i=3 2<4
y=1
5, 1
x=7
i=3
|
 3<4
y=1
7, 1
x=9
i=4 3<4
y=1
7, 1
x=9
i=4
|
 4=4
y=9
9, 9
x=11
i=5 4=4
y=9
9, 9
x=11
i=5
|
5>4
 конец
конец
|
Оператор арифметического цикла. Принципы построения программ с арифметическими циклами можно проиллюстрировать обобщенной блок-схемой (рис. 5.4). Только обрабатывающая часть программы полезна. Остальные операторы являются обслуживающими, необходимыми для организации цикла. Построение цикла способами, описанными выше, неудобно, поэтому рассмотрим специальные операторы цикла, упрощающие этот процесс.
Оператор цикла for:
üFOR переменнаяцикла:= начальноезначение
ТО конечноезначение DO оператор
реализует приращение счетчика циклов на единицу в заданных пределах и контроль его значения. Цикл завершается в момент, когда переменная цикла становится больше конечного значения цикла. Например, оператор:
 FOR a = 3 TO 7 DO WRITELN(a);
FOR a = 3 TO 7 DO WRITELN(a);
дословно интерпретируется следующим образом: “ Оператор WRITELN после слова DO будет повторяться столько раз, сколько нужно, чтобы переменная А, изменяясь с шагом 1 от значения равного 3, достигла 7”. Т.е.: A=3; 4; 5; 6; 7 и цикл будет выполнен 5 раз.
Если после слова DO поместить конструкцию begin...end, цикл может содержать неограниченное число операторов, например
FOR i = 1 TO n DO BEGIN WRITELN(i); READLN(x) END;
Имеется форма оператора, работающего на убывание (шаг равен –1).
üFOR переменнаяцикла:= начальноезначение
DOWNТО конечноезначение DO оператор
В качестве параметров оператора цикла разрешены и выражения, например, FOR c=b+2 TO 4*k DO...
Важно: все параметры в операторе FOR должны быть целого типа.
Задачи на накопление. В практике очень распространены задачи на накопление, т.е. на нахождение сумм и произведений последовательности переменных. Такие задачи могут встречаться как в формулировке итерационных, так и арифметических циклов.
Пример 5-4. Пусть требуется найти сумму N произвольных целых чисел Х. В программе P5_4 сумма накапливается в переменной S с помощью оператора S=S+X. Начальное значение суммы берется равным нулю (S=0).
 |
@ Задание. 5.4. Переделайте программу таким образом, чтобы она вычисляла еще среднее арифметическое и произведение.
 Числовые ряды. Типичной циклической задачей на накопление является вычисление числовых рядов.
Числовые ряды. Типичной циклической задачей на накопление является вычисление числовых рядов.
Здесь каждый следующий член прогрессии Аi равен предыдущему Ai-1, умноженному на два. Если учесть введенные обозначения, можно записать так называемые рекуррентные формулы:
Si = Si-1 + Ai, где Sо=0
Ai = 2Ai-1 A1=3..
Или, как принято в программировании:
S=S+A, S=0
A=2A, A=3
Действие оператора FOR отражено блок-схемой рис. 5.5. Сам оператор FOR помещается в фигуру “прямоугольник в ромбе”, которая имеет два выхода. Выход ДА соответствует случаю, когда переменная цикла £ своему предельному значению (здесь I<=N) – цикл продолжает выполняться. Выход НЕТ – случаю превышения переменной этой границы – цикл завершается.
 |
Аналогично строятся программы для циклического произведения, однако исходное значение искомого произведения берется равным единице. Если по аналогии с суммой сделать его равным нулю, то результат всегда будет также нулем, поскольку умножение на ноль дает только ноль.
 @ Задание. 5.5. Напишите программу вычисления произведения N элементов числового ряда.
@ Задание. 5.5. Напишите программу вычисления произведения N элементов числового ряда.
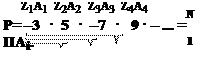 |
Здесь справедливы формулы:
P=PZA, P=1
A=A+2, A=3
Z=–Z, Z=–1
Для формирования изменяющегося знака вводим специальную переменную Z и задаем ей первоначальное значение, совпадающее со знаком первого сомножимого (–1). Далее знак будет изменяться на противоположный при каждом умножении на минус 1 (Z=–Z).
Оператор цикла является сильнейшим средством программиста. Он один заменяет несколько операторов в цикле, построенном обычным образом, а именно: оператор задания исходного значения циклической переменной (или счетчика циклов) и операторы ее приращения и анализа.
Пример 5-6. Для N произвольных целых чисел Х вычислить и отпечатать: 1) сумму отрицательных чисел S, 2) количество положительных чисел КР, 3) произведение положительных чисел Р. Все вычисления производить до появления первого нуля в последовательности. Если ноль не встретился, кроме S, KP и Р, печатать сообщение Нулей нет. Блок-схема алгоритма на рис. 5.6. Проверка в программе сделана для N=5 и Х=3, –2, 1, –3, 2. В результате: S=–5, P=6, KP=3.
@ Задание 5.6. Программа имеет один дефект. Произведение положительных элементов может оказаться равным 1, как в случае, если оно действительно таким получилось, так и если положительных чисел не было совсем (ведь исходное значение произведения =1). Исправьте программу.
| program P5_6; label t; | проверка для n=5 (х=3, –2, 1, –3, 2) | |||||
| var i,n,kp,x,s,p:integer; begin | цикл | цикл | цикл | цикл | цикл | |
| readln(n); kp:=0; s:=0; p:=1; for i:=1 to n do begin readln(x); if x=0 then goto t; if x<0 then s:=s+x; if x>0 then begin kp:=kp+1; p:=p*x end; end; writeln('0 нет'); t: writeln(s,p,kp); end. | n=5 i=1<5 x=3 kp=1 p=3 | 2<5 x=–2 s=–2 | 3<5 x=1 kp=2 p=3 | 4<5 x=–3 s=–5 | 5=5 x=2 kp=3 p=6 | 6>5 0 нет –5,6,3 |
Оператор цикла с предусловием имеет вид
üWHILE условие DO оператор
 Такая конструкция позволяет легко организовывать итерационные циклы (циклы с заранее неизвестным числом повторений). Оператор, входящий в тело цикла выполняется до тех пор, пока истинно условие. Для примера решим задачу – вычислять и печатать Y=Х/2 до обнаружения первого Х=0. Программа приведена ниже.
Такая конструкция позволяет легко организовывать итерационные циклы (циклы с заранее неизвестным числом повторений). Оператор, входящий в тело цикла выполняется до тех пор, пока истинно условие. Для примера решим задачу – вычислять и печатать Y=Х/2 до обнаружения первого Х=0. Программа приведена ниже.
readln(x); {Y=Х/2}
while x<>0 do begin
writeln(х, х/2);
Readln(x)
end; {оператор while}






