Электр өрісінің суперпозиция принципі бойынша:
немесе 
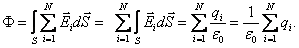
N заряд жүйесінің тұйық бет арқылы электр өрісінің кернеулік векторының ағыны осы бет қамтитын зарядтардың алгебралық қосындысына тура пропорционал.
54-СҰРАҚ
Гаусс теоремасы. Электростатикалық өрісті есептеу әдістері. Гаусс теоремасын әр текті өріс кернеулігі үшін орыс математигі М.В.Остроградский қорытып шығарды. Заряд көлемдік тығыздығы r болатын тұйықталған беттің ішінде үздіксіз таралса, яғни r=dq/dV, онда V көлем ішінде зарядтың шамасы:Sqi= òr dV. Бұдан Гаусс теоремасы Ф= 
(9.18) болып шығады. Енді Гаусс
теоремасын вакуумдағы кейбір электро-
+s -s статикалық өрістер үшін жазайық.
1.Біркелкі зарядталған шексіз жазықтық
өрісі үшін E=s/2 e0(9.19).
2. Әртекті зарядталған екі шексіз парал-
лель жазықтықтар өрісі үшін (28-сурет):
E=0 E=s/ e0 E=0 E=s/ e0 (9.20)- жазықтықтар аралығындағы
қорытқы кернеулік, ал жазықтық сыртында
кернеулік нольге тең.
55-СҰРАҚ
Электрстатикалық өрістердің қасиеттері
1. Электрстатикалық өрісте заряд орын ауыстырғанда орындалатын жұмыс. Нүктелік 
зарядының өрісінде екінші нүктелік заряд 
1-ші нүктеден 2-ші нүктеге қайсыбір траекториямен қозғалсын (12.1-сурет).
12.1-сурет. Электр өрісінің жұмысы
Орындалатын элементар жұмыс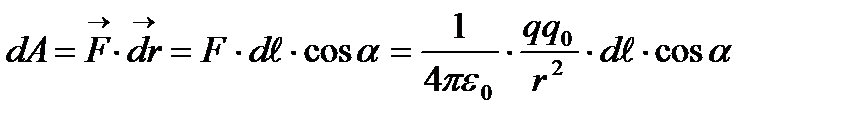 
, 
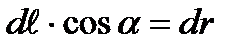болғандықтан, 
болады. 
зарядын 1-ші нүктеден 2-ші нүктеге дейін орын ауыстырғанда орындалатын жұмыс:
, (12.1)
мұндағы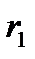 
мен 
- 
зарядынан қозғалушы 
орналасқан бастапқы және соңғы нүктелерге дейінгі қашықтықтар. Осыған сәйкес (11.1) теңдігінен электростатикалық өрісте жұмыс зарядтың жүріп өткен жолының траекториясына байланысты емес екендігін және тек қана 1-ші мен 2-ші нүктелердің орнымен анықталатынын көруге болады. Олай болса, бұл электрстатикалық өріс потенциалды, электрлік күштер консервативті болады деген сөз. Егер бірнеше нүктелік зарядтардың өрісінде қозғалатын болса, оған суперпозиция принципі бойынша,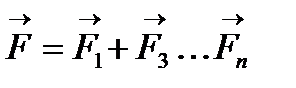 
күші әсер еткендіктен, атқарылатын жұмыс әр күш жұмыстарының алгебралық қосындысына тең, яғни
, (12.2)
бұл жердегі 
мен 
мөлшері 
зарядтан орналасқан бастапқы және соңғы нүктелерге дейінгі қашықтық. Жоғарыдағы (12.2) формуладан туындайтын тағы бір қорытынды –электрстатикалық өрісте зарядтың тұйық контурдың бойымен орын ауыстыру жұмысының нөлге теңдігі, яғни 
болуы. Егер қозғалушы зарядты бірлік өлшемді зарядқа тең деп алсақ, онда (12.2) теңдіктен:
,
немесе 
. (12.3)
Бұл интеграл электрстатикалық өрістің кернеулік векторының тұйық контур бойымен циркуляциясы деп аталады.
векторының циркуляциясы теоремасынан бірнеше маңызды қорытындылар шығаруға болады:
1) электрстатикалық өріс кернеулігінің күш сызықтары тұйық болуы мүмкін емес
Шындығында да, егер векторының қандай да бір сызығы тұйық болса, онда осы сызық бойымен векторының циркуляциясын алсақ (12.3)
теориямен қарама-қайшылыққа келуші едік.
2) 12.2-суретте көрсетілген түрдегі электрстатикалық өрістің болуы мүмкін емес.
12.2-сурет.Электрстатикалық өрістің күш сызықтары тұйықталған болуы
мүмкін емес
Егерде 12.2-суретте көрсетілген үзік-үзік сызықтарға векторының циркуляциясы теоремасын қолданса, онда ол нөлден ерекше болады, ал ол теоремаға қарама-қайшы келеді.
56-СҰРАҚ
Электрстатикалық өріс потенциалы. Потенциалдық өрістегі консервативтік күштер жұмысы потенциалдық энергияның кемуі нәтижесінде орындалатынын ескере отырып, (12.1) теңдеуін былай жазуға болады:
. (12.4)
Демек, зарядының 
заряды өрісіндегі потенциалдық энергиясын:
(12.5)
деп алуға болады. Бұл формуладағы С-тұрақтысын потенциалдық энергияның шексіздіктегі мәні нөлге тең болуы шартынан табуға болады. Осыған сәйкес зарядының 
өрісіндегі потенциалдық энергиясы:
, (12.6)
не екінші жағынан соңғы формуланы -дің өрісінде орналасқан зарядының энергиясы деп те есептеуге болады. (12.6) өрнегінен берілген нүктедегі 
қатынасының -дің мөлшеріне байланысты емес екені байқалады. Сондықтан бұл қатынас - электрстатикалық өрістің энергетикалық сипаттамасы бола алады. Оны өрістің потенциалы деп атайды:
. (12.7)
Бұл формуладан, электрстатикалық өрістің берілген нүктесіндегі потенциалы - сол нүктеде орналасқан бірлік өлшемдегі оң зарядтың потенциалдық энергиясына тең деген қорытынды шығады. Келтірілген (12.6) және (12.7) өрнектерінен нүктелік зарядтың потенциалы
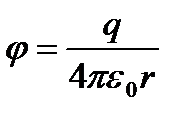(12.8)
екені шығады. Зарядты өрістің бір нүктесінен оның екінші нүктесіне дейін орын ауыстырғанда орындалатын жұмысты (12.8) теңдігін ескере отырып, төмендегідей түрде жазуға болады:
. (12.9)
Бұдан көретініміз, орындалатын жұмыс орын ауыстырушы зарядтың мөлшері мен электрстатикалық өрістің заряд орналасатын бастапқы және соңғы нүктелерінің потенциалдар айырымының көбейтіндісіне тең болады екен. Егер өрісті бір ғана заряд емес, бірнеше 
зарядтар құрайтын болса, онда (12.9) формуласы бойынша, осы өрісте орналасқан -дің потенциалдық энергиясы
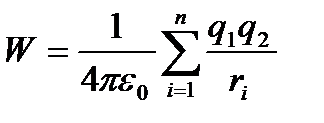, (12.10)
бұдан нүктедегі ізделініп отырған потенциал
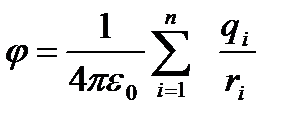(12.11)
болады. Жоғарыдағы (12.10) теңдігімен салыстырғанда, (12.11) өрнегінен зарядтар системасының берілген нүктедегі потенциалы - ол өрістегі әрбір заряд потенциалдарының алгебралық қосындысына тең болатындығы байқалады. Егер зарядтардың берілген көлемдегі тығыздығы 
болса, онда (12.11) теңдігін төмендегідей түрде жазуға болады:
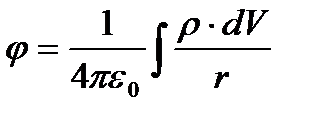. (12.12)
Бұл интеграл зарядтар орналасқан кеңістікті толық қамтиды. Егер зарядтар берілген бір бетте 
беттік тығыздықпен орналасса, онда:
, (12.13)
мұндағы 
- зарядтың беттік тығыздығы; 
- беттік аудан 
-тің элементі
Электрстатикалық өрісті графиктік түрде күш сызықтары арқылы ғана емес эквипотенциалды беттер арқылы да кескіндеуге болады. Эквипотенциалдық беттер деп барлық нүктелерінің потенциалдары бірдей беттерді айтады. Егер өрісті нүктелік заряд тудырса, онда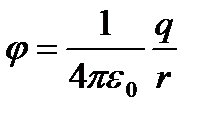 
формуласына сәйкес эквипотенциалдық беттер сфера түрінде болады
12.3-сурет. Эквипотенциалдық беттер.
57-СҰРАҚ
Кернеулік векторы 
мен потенциал 
арасындағы байланыс. 
заряды туғызатын электр өрісінде 
-ші заряды 
осінің бойымен 
қашықтыққа орын ауыстырғанда орындалатын жұмыс 
болсын. Екіншіден, бұл жұмыс 
болады. Олардың оң жақтарын теңестіргенде:
. (12.14)
Дәл осылай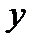 
және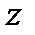 
өстерін қарастыра отырып, 
векторының төмендегідей өрнегіне келеміз
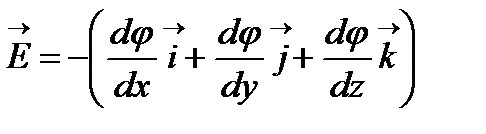, (12.15)
мұндағы 
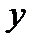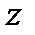- , , – координат осьтері бойымен бағытталған бірлік векторлар.
Градиент туралы анықтамадан:
немесе 
, (12.16)
мұндағы 
- Гамильтон операторы (набла операторы). (12.16) бойынша - кернеулік теріс таңбамен алынған потенциалдың градиентіне тең болады.
Электрстатикалық өрісті графиктік түрде күш сызықтары арқылы ғана емес эквипотенциалды беттер арқылы да кескіндеуге болады. Эквипотенциалдық беттер деп барлық нүктелерінің потенциалдары бірдей беттерді айтады. Егер өрісті нүктелік заряд тудырса, онда 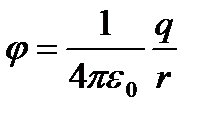формуласына сәйкес эквипотенциалдық беттер сфера түрінде болады (12.3-суретті қара). Нүктелік зарядтың күш сызықтары радиус бойымен бағатталғандығын айтқанбыз, яғни эквипотенциалдық беттер мен күш сызықтары өзара ортогональ болып келеді. Суретте күш сызықтары үзік-үзік сызықтармен жүргізілген. Эквипотенциалды беттердің жиілеуі (қоюлануы) потенциалдың мәнінің өзгеруіне сәйкес келеді. Зарядтан алыстаған сайын эквипотенциалдық беттер сирей береді. Эквипотенциалдық беттердің бағытын біле отырып күш сызықтарын жүргізуге болады немесе керісінше.
12.3-сурет. Эквипотенциалдық беттер.
58-СҰРАҚ
