Ядро, область значений, собственные значения и собственные векторы

ЛИНЕЙНОГО ОПЕРАТОРА

 

Вопросы для самоконтроля:

1.Что такое характеристический корень линейного оператора?

2.Что такое собственное значение и собственный вектор линейного оператора?

3.Как связаны характеристические корни и собственные значения линейного оператора линейного пространства над полем действительных чисел, над полем комплексных чисел?

4.Как найти собственные векторы линейного оператора линейного пространства?

5.Что такое ядро и область значений (образ) линейного оператора? Чему равны их размерности?

6.Как найти базисы ядра и образа линейного оператора?

 

ВАРИАНТ 1

1.Описать образ и ядро оператора дифференцирования пространства многочленов степени £n.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) 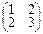; б) .

 

ВАРИАНТ 2

1.В пространстве А₃ линейный оператор φ переводит вектор x=(x₁,x₂,x₃) в вектор φx=(x₁–x₂+x₃, x₁–x₂+x₃, x₁–x₂+x₃). Найти базисы и размерности образа и ядра этого оператора.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .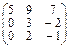

 

 

ВАРИАНТ 3

1.Найти образ и ядро линейного оператора φ в линейном пространстве V₃ векторов-отрезков, заданного формулой φx=[x,a], где а – фиксированный вектор.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 4

1.В пространстве А₃ линейный оператор φ переводит вектор x=(x₁,x₂,x₃) в вектор φx=(2x₁–x₂–x₃, x₁–2x₂+x₃, x₁+x₂–2x₃). Найти базисы и размерности образа и ядра этого оператора.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 5

1.Найти образ и ядро линейного оператора линейного пространства V₃ векторов-отрезков, заданного формулой φx=[a,[x,b]], a и b – фиксированные векторы.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 6

1.В пространстве А₃ линейный оператор φ переводит вектор x=(x₁,x₂,x₃) в вектор φx=(–x₁+x₂+x₃, x₁+x₂–x₃, x₁–x₂+x₃). Найти базисы и размерности образа и ядра этого оператора.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .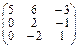

 

ВАРИАНТ 7

1.В пространстве P_n многочленов степени £n задан разностный оператор φ(f(x))=f(x+1) – f(x). Найти образ и ядро этого оператора.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 8

1.В пространстве А₄ линейный оператор φ вектор x=(x₁,x₂,x₃,x₄) переводит в вектор φx=(x₁+x₂–x₃–x₄, x₁+x₂–x₃–x₄, 2x₁+2x₂–2x₃–2x₄, x₁+x₂+2x₃–x₄). Найти базисы и размерности ядра и образа этого оператора.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 9

1.Линейное пространство L является прямой суммой подпространств L₁ и L₂, 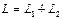; оператор φ, который любому вектору x из L с разложением x=x₁+x₂, x₁ÎL₁, x₂ÎL₂ ставит в соответствие вектор x₁, называется оператором проектирования пространства L на L₁ параллельно L₂. Найти образ и ядро оператора φ.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 10

1.В пространстве многочленов степени £3 дан оператор φ такой, что φ(f(x))=f(x+2) – f(x)/2. Найти его образ и ядро.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 11

1.В пространстве А₄ линейный оператор φ вектор x=(x₁,x₂,x₃,x₄) переводит в вектор φx=(x₁+x₂+x₃–x₄, x₁+x₂+x₃–x₄, x₁+x₂+x₃–x₄, x₁+x₂+x₃–x₄). Найти базисы и размерности ядра и образа этого оператора.

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

 

ВАРИАНТ 12

1.В трехмерном линейном пространстве линейное преобразование φ задается матрицей А. Найти базисы и размерности ядра и образа этого преобразования.

.

 

2.Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

ВАРИАНТ 13

1.В пространстве А₃ оператор φ переводит вектор x=(x₁,x₂,x₃) в вектор φx=(x₁+x₂, x₂, x₁+x₂+x₃). Найти базисы и размерности образа и ядра этого оператора.

2. Найти собственные значения и собственные векторы операторов, заданных матрицами:

а) ; б) .

 

Список литературы

 

1.Шевцов Г.С. Линейная алгебра: теория и прикладные аспекты/ «Финансы и статистика», Москва, 2003.

 

СОДЕРЖАНИЕ

 

Лабораторная работа 8

ЛИНЕЙНОЕ ПРОСТРАНСТВО. ПОДПРОСТРАНСТВО

БАЗИС И РАЗМЕРНОСТЬ. 3

 

Лабораторная работа 9

МАТРИЦА ПЕРЕХОДА. КООРДИНАТЫ ВЕКТОРОВ.. 8

 

Лабораторная работа 10

МАТРИЦА ЛИНЕЙНОГО ОПЕРАТОРА. СВЯЗЬ КООРДИНАТ ВЕКТОРА И ЕГО ОБРАЗА 13

 

Лабораторная работа 11

ОРТОНОРМИРОВАННЫЙ БАЗИС. ОРТОГОНАЛЬНОЕ ДОПОЛНЕНИЕ. ПРОЕКЦИЯ, ПЕРПЕНДИКУЛЯР, НАКЛОННАЯ. ПЛОСКОСТЬ В ЛИНЕЙНОМ ПРОСТРАНСТВЕ 22

 

Лабораторная работа 12

ПОДПРОСТРАНСТВА. СУММА И ПЕРЕСЕЧЕНИЕ ПОДПРОСТРАНСТВ 27

 

Лабораторная работа 13

ЯДРО, ОБЛАСТЬ ЗНАЧЕНИЙ, СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ

ЛИНЕЙНОГО ОПЕРАТОРА.. 32

 

Список литературы.. 37

 

Линейная алгебра: лабораторные работы 8-13

 

Составители: Галина Александровна Маланьина

Яков Давидович Половицкий

Валентина Ивановна Хлебутина

Редактор Н.В. Коваль

Корректор В.Н. Ушакова

 

Подписано в печать 27.07.2006. Формат 60х84 1/16.

Бум.ВХИ. Печать офсетная. Усл. печ. л. 2,32.

Уч.– изд. л. 2,1. Тираж 500 экз. Заказ

 

Редакционно-издательский отдел Пермского университета

614990. Пермь, ул. Букирева, 15

Типография Пермского университета

614990. Пермь, ул. Букирева, 15