Вопросы для самоконтроля:
1.Что называется подпространством линейного пространства?
2.Как найти размерность и базис линейной оболочки конечной системы векторов (то есть подпространства, натянутого на эти векторы)?
3.Что называется суммой подпространств, пересечением подпространств? Чему равна размерность суммы подпространств?
4.Как найти размерность и базис суммы и пересечения подпространств?
5.Когда сумма подпространств называется прямой суммой?
ВАРИАНТ 1
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
x1=(1,1,1,1), y1=(1,-1,-1,1),
x2=(1,1,-1,-1), y2=(2,-2,0,0),
x3=(1,-1,1,-1); y3=(3,-1,1,1).
2.Доказать, что если размерность суммы линейных подпространств пространства Аn на единицу больше размерности их пересечения, то сумма совпадает с одним из этих подпространств, а пересечение – с другим.
ВАРИАНТ 2
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(1,2,1), y1=(2,3,-1),
a2=(1,1,-1), y2=(1,2,2),
a3=(1,3,-3); y3=(1,1,-3).
2.Пусть L, L1, L2 – подпространства пространства Аn. Доказать, что L тогда и только тогда будет прямой суммой L1, L2, когда выполняются условия:
а) L содержит L1, L2;
б) каждый вектор xÎL однозначно представляется в виде x=x1+x2, где x1ÎL1, x2ÎL2.
ВАРИАНТ 3
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
x1=(0,1,1,1), y1=(-1,3,2,-1),
x2=(1,1,1,2), y2=(1,1,0,-1),
x3=(-2,0,1,1); y3=(-1,7,4,-3).
2.Доказать, что сумма S подпространств L1 и L2 тогда и только тогда будет прямой, когда хотя бы один вектор xÎS однозначно представляется в виде x=x1+x2, где x1ÎL1, x2ÎL2.
ВАРИАНТ 4
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(1,1,0,0), y1=(2,2,2,2),
a2=(1,1,2,2), y2=(2,0,1,-1),
a3=(3,1,3,1); y3=(3,1,2,0).
2.Пусть линейное пространство L является прямой суммой подпространств L1, L2. Доказать, что размерность L равна сумме размерностей L1, L2, причем любые базисы L1, L2 дают вместе базис L.
ВАРИАНТ 5
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
x1=(2,-1,0,0,3), y1=(2,1,1,-1,1),
x2=(4,-2,0,0,6), y2=(1,0,1,0,1),
x3=(0,1,1,0,2); y3=(1,1,0,-1,0).
2.Доказать, что сумма L подпространств L1, L2 тогда и только тогда будет прямой, когда объединение базисов этих подпространств дает базис L.
ВАРИАНТ 6
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(1,2,0,1), a2=(1,1,1,0), a3=(3,5,1,2);
b1=(1,0,1,0), b2=(1,3,0,1), b3=(3,6,1,2).
2.Доказать, что в пространстве Pn многочленов степени £n
а) множество L1 четных многочленов f(t) (то есть таких, что f(-t)=f(t)) и множество L2 нечетных многочленов (то есть таких, что f(-t)=-f(t)) являются подпространствами;
б) справедливо равенство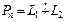 
.
ВАРИАНТ 7
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(1,1,0,0,1,1), a2=(2,1,0,2,1,0), a3=(0,0,2,0,0,-2);
b1=(1,0,0,2,0,-1), b2=(1,1,1,-1,-1,-1), b3=(3,1,1,3,-1,-3).
2.Линейное пространство V разложено в прямую сумму подпространств L1, L2. Доказать:
а) всякий вектор x из V имеет единственное разложение x=x1+x2, где x1ÎL1, x2ÎL2;
б) если вектор x имеет разложение x=x1+x2, x1ÎL1, x2ÎL2, то разложение вектора λx по подпространствам L1, L2 имеет вид λx=λx1+λx2;
в) если y – вектор с разложением y=y1+y2, y1ÎL1, y2ÎL2, то для вектора x+y разложение по пространствам L1, L2 будет x+y=(x1+y1)+(x2+y2).
ВАРИАНТ 8
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(1,-2,1), a2=(0,-3,3), a3=(2,-7,5), a4=(1,-3,2);
b1=(1,0,0), b2=(2,2,0), b3=(0,0,3), b4=(4,4,3).
2.Проверить, что подпространства L1 и L2, натянутые на системы векторов x1=(2,3,11,5), x2=(1,1,5,2), x3=(0,1,1,1) и y1=(2,1,3,2), y2=(1,1,3,4), y3=(5,2,6,2) соответственно, дают в прямой сумме все подпространство A4, и найти разложение вектора x=(2,0,0,3) по этим подпространствам.
ВАРИАНТ 9
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
x1=(1,-1,-1,1), x2=(0,2,2,0), x3=(0,3,2,-1);
y1=(0,1,2,-1), y2=(1,-1,1,1), y3=(2,-1,4,1).
2.Проверить, что симметрические матрицы и кососимметрические матрицы линейного пространства М3 матриц третьего порядка составляют подпространства L1 и L2. Доказать, что пространство М3 является их прямой суммой.
ВАРИАНТ 10
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(1,1,1,1), a2=(1,-1,1,-1), a3=(1,3,1,3);
b1=(1,2,0,2), b2=(1,2,1,2), b3=(3,1,3,1).
2.Доказать, что сумма подпространств L1, L2 будет их прямой суммой в том и только в том случае, если всякая система ненулевых векторов x1, x2, взятых по одному из каждого L1, L2, линейно независима.
ВАРИАНТ 11
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(1,1,0,0), a2=(0,1,1,0), a3=(0,0,1,1);
b1=(1,0,1,0), b2=(0,2,1,1), b3=(1,2,1,2).
2.Проверить, что симметрические матрицы и верхние треугольные матрицы пространства М3 матриц третьего порядка составляют подпространства P и Q. Что представляет собой сумма P+Q и пересечение PÇQ?
ВАРИАНТ 12
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
x1=(1,2,1,-2), x2=(2,3,1,0), x3=(1,2,2,-3);
y1=(1,1,1,1), y2=(1,0,1,-1), y3=(1,3,0,4).
2.Проверить, что в пространстве Pn множество Q={f(x)|f(1)=0} составляет подпространство. Найти такое подпространство R пространства Pn, что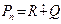 
. Найти разложение вектора 2x2+3x+2 по этим пространствам.
ВАРИАНТ 13
1.Найти базис и размерность суммы и пересечения подпространств, натянутых на векторы:
a1=(2,-5,3,4), a2=(1,2,0,7), a3=(3,-6,2,5);
b1=(2,0,4,6), b2=(1,1,1,1), b3=(3,3,1,5).
2.Доказать, что в пространстве An множества L1={(x1,…,xn)|x1+..+xn=0, x1,...,xnÎR} и L2={(x1,…,xn)|x1=…=xn, x1,…xnÎR} составляют подпространства, и пространство An является их прямой суммой.
Лабораторная работа 13
