АМ сигналдардың -диодтық детекторы үлкен деңгейдегі сигналдармен жұмыс істеу үшін кең қолданылады, бұндай детектор диодты тізбектей және RC-параллель(ол жиілікті фильтірдің жұмысын атқарады) қосылуынан құралады. Шарттарға сәйкес RC- тізбегін мына параметр арқылы таңдайды:
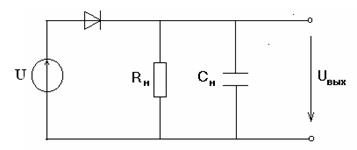
Сурет 7. Амплитуда - диодтық детектор
в) Кд берілген детектерлеу коэффициентін алу үшін Rж жүктеме кедергісін есептеу:
г) f0 және F берілген кездегі Сж детектордың жүктеме сыймдылығының мәнін таңдау:
д) Детектордың кірісі мен шығысындағы кернеу спектрлерін есептеу және тұрғызу:
Сурет 8. Детектордың кірісі мен шығысындағы кернеу спектрлері
Модуляцияланған тербелiстiң түрi келесiдей болады:
;
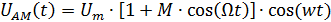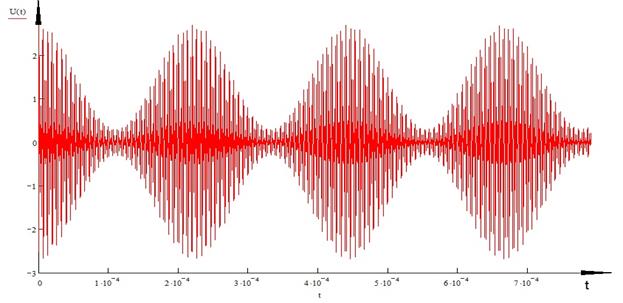
Сурет 9. Модуляциялық тербелістің түрі
Тапсырма
Q (0;1) қарапайым біріншілік коданың кодалық комбинациясы берілген
Талап етіледі:
а) (tтүз=1)бірретті қатені түзете алатындай, оны бөгеуілге төзімді циклдық код ретінде кодерлеу;
б) F(0;1) циклдық коданың кодалық комбинациясының дұрыс тұрғызылуын тексеру;
в) Циклдық коданың синдромдар кестесін құру;
г) Циклдық код кодерінің құрылымдық сұлбасын тұрғызу;
д) Циклдық кодтың кодалық комбинациясының і-ші разрядында бірретті қате түзеле ме, тексеру.
Берілгені:
4-кесте
| Сынақ кітапшасының соңғы саны | |
| Кодалық комбинацияның 1-ші жартысы | |
| Сын кітапшасының соңғы санының алдындағы сан | |
| Кодалық комбинацияның 2-ші жартысы | |
| і қателік разряд номері |
Кодалық комбинация – 1011
Ақпараттық символдар саны k=4
а) (tтүз=1)бірретті қатені түзете алатындай, оны бүгеуілге төзімді циклдық код ретінде кодерлеу:
Минималды кодалық арақашықтық түзетілген қателер саны:
d0=2∙tиспр+1=2∙1+1=3
r тексеру рәміздерінің санын анықтауға арналған, d0=3 кодасы ғана үшін нақты қатынас белгілі екенін ескерген жөн: мұндағы n=k+r. Бұдан k – жай коданың кодалық комбинациясының ұзындығы; n – түзетуші коданың ортақ ұзындығы.
2r≥n+1 n=k+r
2r≥k+r+1=4+r+1=5+r
r=3
n=k+r=4+3=7
Мұндағы
n - кодалық комбинацияның ұзындығы (разрядтардың);
k - кодалық комбинациялардың (разрядтардың) ақпараттық бөлігінің ұзындығы;
r -i қателік разряд номері.
б) F(0;1) циклдық коданың кодалық комбинациясының дұрыс тұрғызылуын тексеру:
Кодалық комбинацияның дұрыс тұрғызылуы құраушы полиномға құрастырылған комбинацияның бөлінуімен тексеріледі. Егер бөлу кезінде нөлдік емес қалдық қалатын болса, бұл алынған кодалық комбинация осы коданың тиым салынған комбинацияларына қатысты нөлдік қалдық алынса дұрыс кодерлеу туралы айтылады:
G(x)=x3+x+1
G(0,1)=1011
Көрсетілген кодалық комбинация есептеудің алгебралық түрде:
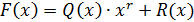
Мұндағы Q(x) – жай кодтың кодалық комбинациясы;
R(x) – бөлудің қалдығы; 
Көрсетілген кодалық комбинация есептеудің алгебралық және цифрлы түрде:
;
;
Циклдік кодтың кодалық комбинациясын есептейік:
Алгебралық түрде:
;
| х6+x4+х3 х6+х 4 +х3 R(X)= 0 | x3+х+1 |
| х3 |
R(x)= 0;
F(x)=Q(x)xr+R(x)=x6+ x4 +х3+ 0
F(0,1)=1011000;
| 1011000 1011 | |
R(0,1)=000
F(0,1)= Q(0,1)xr(0,1)+R(0,1)=1011000+000=1011000;
д) Циклдық кодтың кодалық комбинациясының і-ші разрядында бірретті қате түзеле ме, тексеру:
F(0,1)= 1011000; i = 3 (қате 
болады);
Ендеше:
;
1010000 1101
1101 111
01110
1101
1101
00100
;
Ығысу саны екіге тең болғандықтан, i=2 ендеше бір реттіқате разряды 
. Қате 3-ші жолда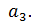 
Осыған сәйкес түзетілген кодтың кодалық комбинациясы 1011000 деген түрге келеді. Ол өз кезегінде бастапқы кодтың кодалық комбинациясына сәйкес.
в) Циклдық коданың синдромдар кестесін құру;
Циклдық кодтың матрицасын тұрғызу: n=7, r=3, k=4, G(x)=x3+x2+1, G(0,1)=1101 болғандықтан:
; 
Осылай келесілерін анықтаймыз:
Туынды матрица G7,4 келесі түрге ие:
| G7,4= | |||||||
Тексеруші матрица H3,4 түрге ие:
| H3,4= | |||||||
Тексеруші матрица құрылған туынды мартицаның дұрыс екендігіне көз жеткізеді.
Синдромдар матрицасы:
| C0,7= | |
| Бұрмаланған рәміз | X6 | X5 | X4 | X3 | X2 | X1 | X0 |
| G1(x)=x3+x2+1 |
5 кесте – синдром мен бұмаланған рәміз арасындағы байланыс
г) Циклдық код кодерінің құрылымдық сұлбасын тұрғызу:
Сурет 10. Циклдық код кодерінің құрылымдық сұлбасы
ҚОРЫТЫНДЫ
Есептік-сызбалық жұмыста телекоммуникациялық жүйелер мен желілерді тұрғызу ұстанымдарын, телекоммуникациялық жүйелердегі акпаратты берудің негізгі заңдылықтарын оқып үйрендім, сонымен қатар негізгі концепцияларды, модельдерді және бөгеуілге төзімді кодерлеу әдістермен, хабарды оптималды қабылдаумен, көпарналы тарату ұстанымдарымен, байланыс жүйесінің оптимизация сұрақтарымен, телекоммуникация облысындағы стандарттар мен қазіргі кезде өсу қарқынымен таныстым. Курстың тапсырмасы – пәнді оқып – үйрену нәтижесінде студенттерде телекомуникациялық жүйелердің бөгеуілге төзімділігі және өткізгіштік қасиеттің шекті мүмкіншітіктерін бағалау, дабылдардың түрленуімен өңделуі, электрлік дабылдардың математикалық талдау жүргізуге мүмкіншілік беретін талаптар мен білімдер қалыптастырдым.
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР
1. Гоноровский И.С. Радиотехнические цепи и сигналы – М.: Радио и связь,
1986 – 607с.
2. Васильев Д.В., Витоль М.Р., Горшенков Ю.Н., и др. Радиотехнические
цепи и сигналы: Учеб. Пос. для вузов. – М.: Радио и связь, 1982.-528с.
3. Баскаков С.Н. Радиотехнические цепи и сигналы: Учеб. Для вузов. – М.:
ВЫСШ. ШК., 2000.
4. Панфилов И.П. Дырда В.Е., Теория электрической связи. Учебник для
техникумов, Москва 1991.
5.Теория электрической связи:Учебник для вузов/Зюко А. Г., Кловский Д. Д.,
Коржик В. И., Назаров М.В.- М.: Радио и связь, 1999.
6. Зюко А. Г., Кловский Д. Д., Назаров М. В., Финк Л. М. Теория передачи
сигналов.- М.:Радио и связь, 1986.
7. Кловский Д. Д. Теория передачи сигналов.- М.: Радио и связь, 1973.
8. Баскаков С. И. Радиотехнические цепи и сигналы. Руководство к решению
задач.- М.: Высшая, 2002
9. Нефедов В. И. Основы радиоэлектроники и связи. М.: Высшая школа, 2002
10. Емельянов Г. А., Шварцман В. О. Передача дискретной информации. М.:
Радио и Связь,1982
