Цель:Научиться находить предел функции в точке и на бесконечности; раскрывать

Практическая работа № 4

По дисциплине «Математика»

для студентов очно – заочного отделения

Тема: Вычисление предела функции в точке. Вычисление предела функции на бесконечности.

Раскрытие неопределенностей.

Цель:Научиться находить предел функции в точке и на бесконечности; раскрывать

неопределенности вида

Перечень необходимых сведений из теории:

1. Предел функции в точке по Коши и Гейне.
2. Свойства предела.
3. Односторон­ние пределы функции в точке. Теорема о существовании двустороннего предела функции в точке.
4. Предел суммы, произведения и частного двух функций.
5. Предел функции на бесконечности.
6. Первый и второй замечатель­ные пределы и следствия из них.

Образец выполнения задания:

Так как знаменатель дроби при х=2 отличен от нуля, то по правилу нахождения предела дробно-рациональной функции получим: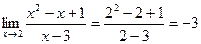

Здесь предел делителя равен нулю: . Следовательно, теорему о пределе частного применить нельзя. Т.к. 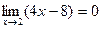то при есть величина бесконечно малая, а обратная ей величина 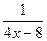- бесконечно большая. Поэтому при произведение есть величина бесконечно большая, т.е ее предел равен бесконечности

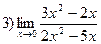
Здесь пределы числителя и знаменателя при 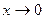равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислять предел нельзя, т.к. при 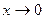получается отношение двух бесконечно малых величин.

Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент стремится к своему предельному значению, никогда не принимая этого значения, поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем:

Пределы числителя и знаменателя при равны нулю:

Разложим квадратный трехчлен в числителе на линейные множители по формул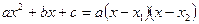е: , где – корни трехчлена. Разложив на множители и знаменатель, сократим дробь на . Используя следствие 4, получим:

Пределы числителя и знаменателя при 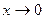равны нулю. Умножив числитель и знаменатель на сопряженный знаменателю множитель а затем сократив дробь на х, получим:

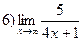
При 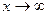знаменатель неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина – бесконечно малой. Произведение бесконечно малой на ограниченную величину есть величина бесконечно малая, и предел ее при 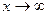равен нулю, следовательно:

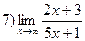
При 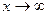числитель и знаменатель величины бесконечно большие. Поэтому при применении теоремы 3 получаем неопределенность . Для вычисления предела этой функции нужно числитель и знаменатель разделить на х (при 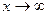слагаемые3/х и 1/х – величины бесконечно малые, и следовательно их пределы равны нулю):

Разделим числитель и знаменатель на наивысшую степень аргумента в знаменателе, т.е. на х³:

Задания для выполнения в аудитории: Вычислите предел функции:

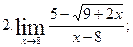
Задания для самостоятельного выполнения Вычислите предел функции.

Исходные данные по вариантам

	2.
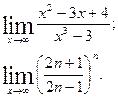
	4.
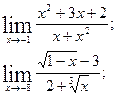
	6.
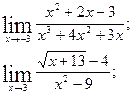
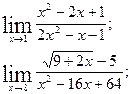
7.	8.
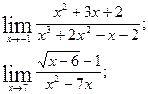
9.	10.

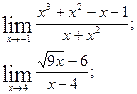
В результате выполнения практической работы студент должен:

знать:

- определение предела функции в точке;

- свойства предела;

- первый и второй замечательные пределы;

уметь:

- вычислять пределы функции в точке и на бесконечности;

- раскрывать неопределенности вида { }, { }, { },{ }.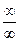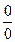