б) прямыми 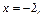

 и графиком функции
и графиком функции
 .
.
Вариант 14.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; ;
| б)  . .
|
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; ;
| б) 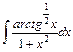 . .
|
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а) 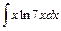 ; ;
| б)  . .
|
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; ;
| б) 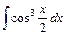 . .
|
5. Найдите неопределённые интегралы:
а)  ; ;
| б) 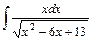 . .
|
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; ;
| б)  dx. dx.
|
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а) 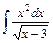 ; ;
| б)  . .
|
8. Вычислитe определённый интеграл:
a)  ; ;
| б)  . .
|
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
 .
.
10. Вычислитe определённый интеграл, используя указанную замену переменной:
 ,
, 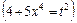 .
.
11. Вычислитe несобственные интегралы либо докажите их расходимость:
а)  ; ;
| б)  . .
| |||
12. Вычислитe площадь фигуры, ограниченной линиями:
а) 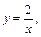

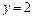 ,
,
б) прямыми 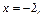

 и графиком функции
и графиком функции
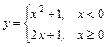 .
.
Вариант 15.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; ;
| б)  . .
|
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а) 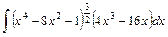 ; ;
| б)  . .
|
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; ;
| б)  . .
|
4. Найти неопределённые интегралы от тригонометрических функций:
а) 
| б) 
|
5. Найдите неопределённые интегралы:
а)  ; ;
| б)  . .
|
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; ;
| б)  dx. dx.
|
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а) 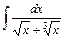 ; ;
| б)  . .
|
8. Вычислитe определённый интеграл:
a)  ; ;
| б)  . .
|
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
.
10. Вычислитe определённый интеграл, используя указанную замену переменной:
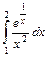 ,
,  .
.
11. Вычислитe несобственные интегралы либо докажите их расходимость:
а)  ; ;
| б) 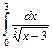 . .
| |||
12. Вычислитe площадь фигуры, ограниченной линиями:
а) 
 ,
,
б) прямыми 

 и графиком функции
и графиком функции
 .
.
Вариант 16.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а) 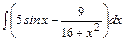 ; ;
| б)  . .
|
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; ;
| б)  . .
|
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; ;
| б)  . .
|
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; ;
| б)  . .
|
5. Найдите неопределённые интегралы:
а) 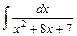 ; ;
| б)  . .
|
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а) 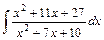 ; ;
| б) 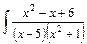 dx. dx.
|
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; ;
| б)  . .
|
8. Вычислитe определённый интеграл:
a)  ; ;
| б)  . .
|
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
 .
.
10. Вычислитe определённый интеграл, используя указанную замену переменной:
 ,
,  .
.
11. Вычислитe несобственные интегралы либо докажите их расходимость:
а)  ; ;
| б)  . .
| |||
12. Вычислитe площадь фигуры, ограниченной линиями:
а) 
 ,
,
б) прямыми 

 и графиком функции
и графиком функции
 .
.
Вариант 17.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; ;
| б)  . .
|
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; ;
| б)  . .
|
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; ;
| б)  . .
|
4. Найдите неопределённые интегралы от тригонометрических функций:
а) 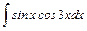 ; ;
| б)  . .
|
5. Найдите неопределённые интегралы:
а)  ; ;
| б) 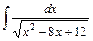 . .
|
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а) 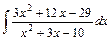 ; ;
| б)  dx. dx.
|
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; ;
| б)  . .
|
8. Вычислитe определённый интеграл:
a)  ; ;
| б)  . .
|
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
.
10. Вычислитe определённый интеграл, используя указанную замену переменной:
 ,
,  .
.
11. Вычислитe несобственные интегралы либо докажите их расходимость:
а)  ; ;
| б)  . .
| |||
12. Вычислитe площадь фигуры, ограниченной линиями:
а) 
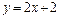 ,
,
б) прямыми 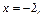

 и графиком функции
и графиком функции
 .
.
Вариант 18.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а) 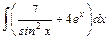 ; ;
| б)  . .
|
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; ;
| б) 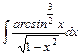 . .
|
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; ;
| б)  . .
|
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; ;
| б)  . .
|
5. Найдите неопределённые интегралы:
а)  ; ;
| б) 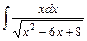 . .
|
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; ;
| б)  dx. dx.
|
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а) 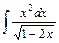 ; ;
| б)  . .
|
8. Вычислитe определённый интеграл:
a) 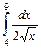 ; ;
| б)  . .
|
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
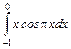 .
.
10. Вычислитe определённый интеграл, используя указанную замену переменной:
 ,
,  .
.
11. Вычислитe несобственные интегралы либо докажите их расходимость:
а)  ; ;
| б) 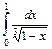 . .
| |||
12. Вычислитe площадь фигуры, ограниченной линиями:
а) 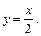
 ,
,
б) прямыми 

 и графиком функции
и графиком функции
 .
.
Вариант 19.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а)  ; ;
| б) 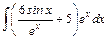 . .
|
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; ;
| б)  dx. dx.
|
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а) 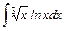 ; ;
| б) 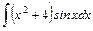 . .
|
4. Найдите неопределённые интегралы от тригонометрических функций:
а) 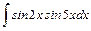 ; ;
| б)  . .
|
5. Найдите неопределённые интегралы:
а) 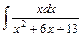 ; ;
| б)  . .
|
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а)  ; ;
| б)  dx. dx.
|
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; ;
| б) 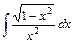 . .
|
8. Вычислитe определённый интеграл:
a)  ; ;
|
б)  . .
|
9. Вычислитe определённый интеграл, используя формулу интегрирования по частям:
 .
.
10. Вычислитe определённый интеграл, используя указанную замену переменной:
 ,
,  .
.
11. Вычислитe несобственные интегралы либо докажите их расходимость:
а)  ; ;
| б)  . .
| |||
12. Вычислитe площадь фигуры, ограниченной линиями:
а) 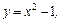
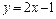 ,
,
б) прямыми 

 и графиком функции
и графиком функции
 .
.
Вариант 20.
1. Найдите неопределённые интегралы, непосредственно интегрируя:
а) 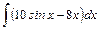 ; ;
| б) 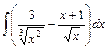 . .
|
2. Найдите неопределённые интегралы методом подведения под знак дифференциала:
а)  ; ;
| б)  . .
|
3. Найдите неопределённые интегралы, используя формулу интегрирования по частям:
а)  ; ;
| б)  . .
|
4. Найдите неопределённые интегралы от тригонометрических функций:
а)  ; ;
| б)  . .
|
5. Найдите неопределённые интегралы:
а)  ; ;
| б) 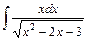 . .
|
6. Найдите неопределённые интегралы от дробно-рациональных функций:
а) 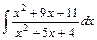 ; ;
| б) 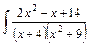 dx. dx.
|
7. Найдите неопределённые интегралы, применив необходимую замену переменной:
а)  ; ;
| б)  . .
|
8. Вычислитe определённый интеграл:
a) 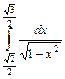 ; ;
|
б) 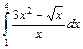 . .
|




