ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками в состоянии с квантовым числом n = 4. Если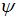 
-функция электрона в этом состоянии имеет вид, указанный на рисунке, то вероятность обнаружить электрон в интервале от 
до 
равна …
| 
| 
| |
| 
| ||
|
| 
| ||
|
| 
|
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Стационарное уравнение Шредингера имеет вид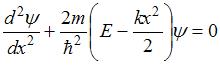 
.
Это уравнение описывает …
|
|
| линейный гармонический осциллятор | |
|
| движение свободной частицы | ||
|
| электрон в трехмерном потенциальном ящике | ||
|
| электрон в водородоподобном атоме |
Решение:
Стационарное уравнение Шредингера в общем случае имеет вид 
. Здесь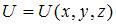 
– потенциальная энергия микрочастицы. В данной задаче 
соответствует гармоническому осциллятору, то есть движению частицы под действием квазиупругой силы. Следовательно, данное уравнение описывает движение частицы под действием квазиупругой силы, то есть линейный гармонический осциллятор.
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Если молекула водорода, позитрон, протон и 
-частица имеют одинаковую длину волны де Бройля, то наибольшей скоростью обладает …
|
|
| позитрон | |
|
| молекула водорода | ||
|
| протон | ||
|
| -частица
|
Решение:
Длина волны де Бройля определяется формулой 
, где 
– постоянная Планка, 
и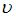 
– масса и скорость частицы. Отсюда скорость частицы равна 
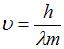. По условию задания 
, следовательно, 
. Тогда наибольшей скоростью обладает частица с наименьшей массой. Известно, что 
. Следовательно, наибольшей скоростью обладает позитрон.
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
Закон сохранения момента импульса накладывает ограничения на возможные переходы электрона в атоме с одного уровня на другой (правило отбора). В энергетическом спектре атома водорода (см. рис.) запрещенным является переход …
|
|
| 
| |
|
| 
| ||
|
| 
| ||
|
| 
|
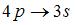
Решение:
Для орбитального квантового числа l существует правило отбора 
. Это означает, что возможны только такие переходы, в которых l изменяется на единицу. Поэтому запрещенным переходом является переход , так как в этом случае 
.
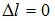ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Нестационарным уравнением Шредингера является уравнение …
|
|
| 
| |
|
| 
| ||
|
| 
| ||
|
| 
|
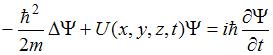
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
В результате туннельного эффекта вероятность прохождения частицей потенциального барьера увеличивается с …
|
|
| уменьшением массы частицы | |
|
| увеличением ширины барьера | ||
|
| уменьшением энергии частицы | ||
|
| увеличением высоты барьера |
Решение:
Вероятность прохождения частицей потенциального барьера прямоугольной формы или коэффициент прозрачности определяется формулой: 
где 
постоянный коэффициент, близкий к единице, 
ширина барьера, 
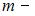масса частицы, 
высота барьера, 
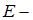энергия частицы. Следовательно, вероятность прохождения увеличивается с уменьшением массы частицы.
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
Собственные функции электрона в атоме водорода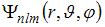 
содержат три целочисленных параметра: n, l и m. Параметр n называется главным квантовым числом, параметры l и m – орбитальным (азимутальным) и магнитным квантовыми числами соответственно. Магнитное квантовое число m определяет …
|
|
| проекцию орбитального момента импульса электрона на некоторое направление | |
|
| энергию электрона в атоме водорода | ||
|
| модуль орбитального момента импульса электрона | ||
|
| модуль собственного момента импульса электрона |
Решение:
Магнитное квантовое число m определяет проекцию орбитального момента импульса электрона на некоторое направление: 
, причем 
.
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Время жизни атома в возбужденном состоянии 10 нс. Учитывая, что постоянная Планка 
, ширина энергетического уровня (в эВ) составляет не менее …
|
|
| 
| |
|
| 
| ||
|
| 
| ||
|
| 
|
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Стационарное уравнение Шредингера имеет вид .
Это уравнение описывает движение …
|
|
| частицы в трехмерном бесконечно глубоком потенциальном ящике | |
|
| частицы в одномерном бесконечно глубоком потенциальном ящике | ||
|
| линейного гармонического осциллятора | ||
|
| электрона в водородоподобном атоме |
Решение:
Бесконечная глубина ящика (ямы) означает, что потенциальная энергия частицы внутри ящика равна нулю, а вне ящика – бесконечности. Таким образом, 
0. Поэтому движение частицы в трехмерном бесконечно глубоком потенциальном ящике описывает уравнение .
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса 
электрона. На рисунке приведены возможные ориентации вектора .
Значение орбитального квантового числа и минимальное значение главного квантового числа для указанного состояния соответственно равны …
|
|
|  , 
| |
|
| , 
| ||
|
|  , 
| ||
|
| , 
|
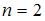
Решение:
Магнитное квантовое число m определяет проекцию вектора орбитального момента импульса на направление внешнего магнитного поля: 
, где 
(всего 2 l + 1 значений). Поэтому для указанного состояния . Квантовое число l не может превышать n – 1. Поэтому минимальное значение главного квантового числа .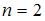
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
На рисунке дана схема энергетических уровней атома водорода, а также условно изображены переходы электрона с одного уровня на другой, сопровождающиеся излучением кванта энергии. В ультрафиолетовой области спектра эти переходы дают серию Лаймана, в видимой области – серию Бальмера, в инфракрасной области – серию Пашена и т.д.
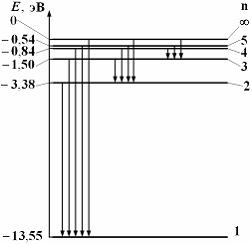
Отношение минимальной частоты линии в серии Бальмера 
к максимальной частоте линии в серии Лаймана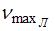 
спектра атома водорода равно …
|
|
| 
| |
|
| 
| ||
|
| 
| ||
|
| 
|
Решение:
Серию Лаймана дают переходы на первый энергетический уровень, серию Бальмера – на второй уровень. Максимальная частота линии в серии Лаймана 
. Минимальная частота линии в серии Бальмера 
. Тогда 
.
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Если протон и -частица прошли одинаковую ускоряющую разность потенциалов, то отношение их длин волн де Бройля равно …
|
|
| 
| |
|
| |||
|
| |||
|
| 
|
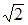
Решение:
-частица – это ядро атома гелия, состоящее из двух протонов и двух нейтронов. Длина волны де Бройля определяется по формуле 
, где p – импульс частицы. Импульс частицы можно выразить через ее кинетическую энергию: 
. По теореме о кинетической энергии, согласно которой работа сил электрического поля идет на приращение кинетической энергии, 
. Отсюда можно найти 
, полагая, что первоначально частица покоилась: 
Окончательное выражение для длины волны де Бройля через ускоряющую разность потенциалов имеет вид: 
Учитывая, что 
и 
отношение длин волн де Бройля протона и -частица равно: 
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса электрона. На рисунке приведены возможные ориентации вектора .
Величина орбитального момента импульса (в единицах 
) для указанного состояния равна …
|
|
| 
| |
|
| 
| ||
|
| |||
|
|
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Стационарное уравнение Шредингера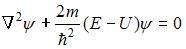 
описывает движение свободной частицы, если потенциальная энергия 
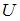имеет вид …
|
|
| 
| |
|
| 
| ||
|
| 
| ||
|
| 
|
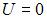
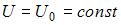
Решение:
Стационарное уравнение Шредингера в общем случае имеет вид 
Здесь 
– потенциальная энергия частицы. Свободной называется частица, не подверженная действию силовых полей. Это означает, что 
В этом случае приведенное уравнение Шредингера описывает движение свободной частицы.
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
На рисунке дана схема энергетических уровней атома водорода.
Наибольшая длина волны спектральной линии (в нм) серии Лаймана равна …
(h = 6,63·10-34 Дж·с)
|
|
| ||
|
| |||
|
| |||
|
|
Решение:
Серию Лаймана дают переходы в состояние с n = 1. Учитывая связь длины волны и частоты 
и правило частот Бора 
, можно сделать вывод о том, что линии с наибольшей длиной волны (то есть с наименьшей частотой) в серии Лаймана соответствует переход со второго энергетического уровня. Тогда 
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Отношение неопределенностей проекций скоростей нейтрона и α-частицы на некоторое направление при условии, что соответствующие координаты частиц определены с одинаковой точностью, равно …
|
|
| ||
|
| 
| ||
|
| |||
|
| 
|
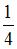
Решение:
Из соотношения неопределенностей Гейзенберга для координаты и соответствующей компоненты импульса 
следует, что 
Здесь 
– неопределенность координаты, 
– неопределенность x-компоненты импульса,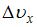 
– неопределенность x-компоненты скорости, – масса частицы; – постоянная Планка, деленная на 
. Неопределенность x-компоненты скорости можно найти из соотношения 
Поскольку соответствующие координаты частиц определены с одинаковой точностью, то есть 
с учетом того, что 
искомое отношение равно: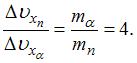 
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Стационарное уравнение Шредингера в общем случае имеет вид . Здесь 
потенциальная энергия микрочастицы. Электрону в одномерном потенциальном ящике с бесконечно высокими стенками соответствует уравнение …
|
|
| 
| |
|
|
| ||
|
|
| ||
|
| 
|
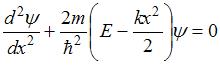
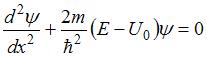
Решение:
Для одномерного случая 
. Кроме того, внутри потенциального ящика U = 0, а вне ящика частица находиться не может, так как его стенки бесконечно высоки. Поэтому уравнение Шредингера для частицы в одномерном ящике с бесконечно высокими стенками имеет вид .
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Отношение скоростей протона и α-частицы, длины волн де Бройля которых одинаковы, равно …
|
|
| ||
|
| |||
|
|
| ||
|
|
|
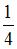
Решение:
Длина волны де Бройля определяется формулой , где – постоянная Планка, и 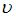– масса и скорость частицы соответственно. Отсюда скорость частицы 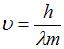. По условию задания 
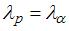; тогда с учетом того, что 
, искомое отношение 
.
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса электрона. На рисунке приведены возможные ориентации вектора .
Величина орбитального момента импульса (в единицах ) для указанного состояния равна …
|
|
|
| |
|
|
| ||
|
| |||
|
|
Решение:
Магнитное квантовое число m определяет проекцию вектора орбитального момента импульса на направление внешнего магнитного поля , где (всего 2 l + 1 значений). Поэтому для указанного состояния . Величина момента импульса электрона определяется по формуле 
. Тогда 
(в единицах ).
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
На рисунке представлена диаграмма энергетических уровней атома водорода:
Излучение фотона с наименьшей длиной волны происходит при переходе, обозначенном стрелкой под номером …
|
|
| ||
|
| |||
|
| |||
|
| |||
|
|
Решение:
Излучение фотона происходит при переходе электрона с более высокого энергетического уровня на более низкий. Учитывая связь длины волны и частоты 
и правило частот Бора , получаем 
. Отсюда можно сделать вывод о том, что излучение фотона с наименьшей длиной волны (то есть с наибольшей частотой) происходит при переходе электрона с энергетического уровня Е4 на уровень Е1, что соответствует переходу, обозначенному стрелкой под номером 3.
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
На рисунке представлена диаграмма энергетических уровней атома водорода:
Излучение фотона с наименьшей длиной волны происходит при переходе, обозначенном стрелкой под номером …
|
|
| ||
|
| |||
|
| |||
|
| |||
|
|
Решение:
Излучение фотона происходит при переходе электрона с более высокого энергетического уровня на более низкий. Учитывая связь длины волны и частоты и правило частот Бора , получаем . Отсюда можно сделать вывод о том, что излучение фотона с наименьшей длиной волны (то есть с наибольшей частотой) происходит при переходе электрона с энергетического уровня Е4 на уровень Е1, что соответствует переходу, обозначенному стрелкой под номером 3.
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Высокая монохроматичность лазерного излучения обусловлена относительно большим временем жизни электронов в метастабильном состоянии, равном
. Учитывая, что постоянная Планка 
, ширина метастабильного уровня будет не менее …
|
|
| 
| |
|
| 
| ||
|
| 
| ||
|
| 
|
Решение:
Соотношение неопределенностей для энергии и времени имеет вид 
, где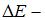 
неопределенность в задании энергии (ширина энергетического уровня), 
время жизни частицы в данном состоянии. Тогда 
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Стационарное уравнение Шредингера в общем случае имеет вид . Здесь потенциальная энергия микрочастицы. Электрону в одномерном потенциальном ящике с бесконечно высокими стенками соответствует уравнение …
|
|
|
| |
|
|
| ||
|
|
| ||
|
|
|
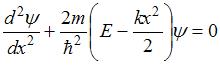
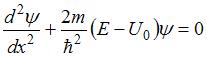
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса электрона. На рисунке приведены возможные ориентации вектора .
Величина орбитального момента импульса (в единицах ) для указанного состояния равна …
|
|
|
| |
|
|
| ||
|
| |||
|
|
Решение:
Магнитное квантовое число m определяет проекцию вектора орбитального момента импульса на направление внешнего магнитного поля , где (всего 2 l + 1 значений). Поэтому для указанного состояния . Величина момента импульса электрона определяется по формуле . Тогда (в единицах ).
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Уравнения Шредингера (общие свойства)
Стационарное уравнение Шредингера в общем случае имеет вид . Здесь 
потенциальная энергия микрочастицы. Трехмерное движение свободной частицы описывает уравнение …
|
|
|
| |
|
| 
| ||
|
|
| ||
|
| 
|
Решение:
Свободной называется частица, не подверженная действию силовых полей. Это означает, что 
. Поэтому трехмерное движение свободной частицы описывает уравнение .
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга
Отношение скоростей протона и α-частицы, длины волн де Бройля которых одинаковы, равно …
|
|
| ||
|
| |||
|
|
| ||
|
|
|
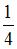
Решение:
Длина волны де Бройля определяется формулой , где – постоянная Планка, и 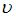– масса и скорость частицы соответственно. Отсюда скорость частицы 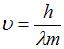. По условию задания 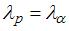; тогда с учетом того, что , искомое отношение .
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
Собственные функции электрона в атоме водорода 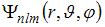содержат три целочисленных параметра: n, l и m. Параметр n называется главным квантовым числом, параметры l и m – орбитальным (азимутальным) и магнитным квантовыми числами соответственно. Орбитальное квантовое число l определяет …
|
|
| модуль орбитального момента импульса электрона | |
|
| энергию электрона в атоме водорода | ||
|
| проекцию орбитального момента импульса электрона на некоторое направление | ||
|
| модуль собственного момента импульса электрона |
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
На рисунках схематически представлены графики распределения плотности вероятности по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний электрона с различными значениями главного квантового числа n:
В состоянии с n = 2 вероятность обнаружить электрон в интервале от 
до 
равна …
|
|
|
| |
|
|
| ||
|
| 
| ||
|
|
|
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Спектр атома водорода. Правило отбора
На рисунке дана схема энергетических уровней атома водорода.
Наименьшая длина волны спектральной линии (в нм) серии Пашена равна _____.
(h = 6,63·10-34 Дж·с)
|
|
| ||
|
| |||
|
| |||
|
|
Решение:
Серию Пашена дают переходы в состояние с n = 3. Учитывая связь длины волны и частоты и правило частот Бора , можно сделать вывод о том, что линии с наименьшей длиной волны (то есть с наибольшей частотой) в серии Пашена соответствует переход с энергетического уровня Е = 0. Тогда 
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Уравнение Шредингера (конкретные ситуации)
Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса электрона. На рисунке приведены возможные ориентации вектора .
Минимальное значение главного квантового числа n для указанного состояния равно …
|
|
| |||||
|
| ||||||
|
|
|
|
|
|
|
|
Дата добавления: 2017-01-28; Мы поможем в написании ваших работ!; просмотров: 2323 | Нарушение авторских прав
Лучшие изречения:
| 2173 - 
Ген: 0.179 с.