 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Уравнения Максвелла
Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид:
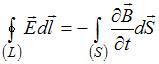 ,
,
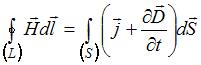 ,
,
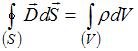 ,
,
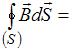 0.
0.
Следующая система уравнений:
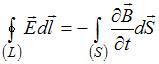 ,
,
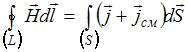 ,
,
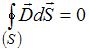 ,
,
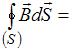 0 –
0 –
справедлива для …

| 
| электромагнитного поля в отсутствие свободных зарядов | |

| электромагнитного поля в отсутствие свободных зарядов и токов проводимости | ||

| электромагнитного поля в отсутствие токов проводимости | ||

| стационарных электрических и магнитных полей |
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Законы постоянного тока
Электропроводка должна выполняться из достаточно толстого провода, чтобы он сильно не нагревался и не создавал угрозы пожара. Если проводка рассчитана на максимальную силу тока 16 А и на погонном метре провода должно выделяться не более 2 Вт тепла, то диаметр медного провода (с учетом того, что удельное сопротивление меди равно 17 нОм·м) равен ______ мм.

| 
| 1,7 | |

| 0,83 | ||

| 1,5 | ||

| 0,97 |
Решение:
Мощность тока 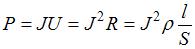 . Тогда мощность, выделяющаяся на погонном метре провода,
. Тогда мощность, выделяющаяся на погонном метре провода,  . Отсюда диаметр провода
. Отсюда диаметр провода 
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Магнитостатика
Электрон влетает в магнитное поле, создаваемое прямолинейным длинным проводником с током в направлении, параллельном проводнику (см. рис.).

При этом сила Лоренца, действующая на электрон, …

| 
| лежит в плоскости чертежа и направлена влево | |

| лежит в плоскости чертежа и направлена вправо | ||

| перпендикулярна плоскости чертежа и направлена «от нас» | ||

| перпендикулярна плоскости чертежа и направлена «к нам» |
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Электрические и магнитные свойства вещества
Вещество является однородным изотропным диамагнетиком, если …

| 
| магнитная восприимчивость мала, вектор намагниченности направлен в сторону, противоположную направлению внешнего магнитного поля | |

| магнитная восприимчивость мала, вектор намагниченности направлен в ту же сторону, что и внешнее магнитное поле | ||

| магнитная восприимчивость велика, вектор намагниченности направлен в ту же сторону, что и внешнее магнитное поле | ||

| магнитная восприимчивость велика, вектор намагниченности направлен в сторону, противоположную направлению внешнего магнитного поля |
КОЛЕБАНИЯ И ВОЛНЫ
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Волны. Уравнение волны
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 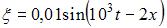 . Амплитуда ускорения колебаний частиц среды (в
. Амплитуда ускорения колебаний частиц среды (в  ) равна …
) равна …

| 
| 
| |

| |||

| |||

|
Решение:
Уравнение плоской синусоидальной волны имеет вид  , где
, где  – амплитуда волны;
– амплитуда волны;  – циклическая частота;
– циклическая частота;  – период колебаний;
– период колебаний; 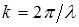 – волновое число;
– волновое число; 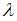 – длина волны; (
– длина волны; (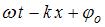 ) – фаза волны;
) – фаза волны;  начальная фаза. Скорость колебаний частиц среды
начальная фаза. Скорость колебаний частиц среды  . Ускорение частиц среды
. Ускорение частиц среды  . Амплитуда ускорения частиц среды
. Амплитуда ускорения частиц среды 
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Энергия волны. Перенос энергии волной
Если в электромагнитной волне, распространяющейся в вакууме, значение напряженности электрического поля равно:  , объемная плотность энергии
, объемная плотность энергии  , то напряженность магнитного поля составляет _______
, то напряженность магнитного поля составляет _______ 
5 | 
|
Решение:
Плотность потока энергии электромагнитной волны (вектор Умова – Пойнтинга) равна:  . Также
. Также  где
где  объемная плотность энергии,
объемная плотность энергии,  скорость света. Следовательно,
скорость света. Следовательно,  .
.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Сложение гармонических колебаний
Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами  .Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
.Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
1. 
2. 
3. 

| |||

| 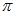
| ||
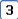
| 
| ||

| 
|
Решение:
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле  , где
, где  и
и 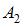 – амплитуды, (
– амплитуды, (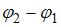 ) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания
) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания 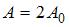 , то
, то  . Тогда
. Тогда  и разность фаз будет равна
и разность фаз будет равна 
Если  , то
, то  . Тогда
. Тогда 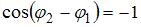 ; следовательно,
; следовательно, 
Если 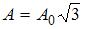 , то
, то  . Тогда
. Тогда  ; следовательно,
; следовательно, 
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Свободные и вынужденные колебания
На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону:
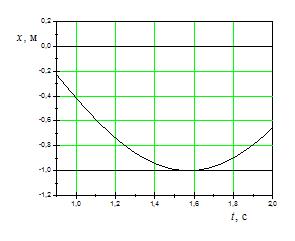

Циклическая частота колебаний точки (в  ) равна …
) равна …
2 | 
|
Решение:
При гармонических колебаниях смещение точки от положения равновесия изменяется со временем по закону синуса или косинуса. Пусть  . Скорость есть первая производная по времени от смещения точки:
. Скорость есть первая производная по времени от смещения точки: 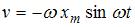 . Отсюда амплитудное значение скорости
. Отсюда амплитудное значение скорости  . Отсюда
. Отсюда  . Приведенные графики позволяют найти
. Приведенные графики позволяют найти  и
и  . Тогда циклическая частота колебаний точки
. Тогда циклическая частота колебаний точки  .
.
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Волны. Уравнение волны
Световые волны в вакууме являются …

| 
| поперечными | |

| продольными | ||

| упругими | ||

| волнами, скорость распространения которых в веществе больше, чем в вакууме |
Решение:
Световые волны – электромагнитные волны. В электромагнитной волне векторы напряженностей электрического и магнитного полей колеблются в плоскостях, перпендикулярных направлению распространения волны, следовательно, световые волны являются поперечными.
 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Свободные и вынужденные колебания
На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону:


Циклическая частота колебаний точки (в  ) равна …
) равна …
2 | 
|
Решение:
При гармонических колебаниях смещение точки от положения равновесия изменяется со временем по закону синуса или косинуса. Пусть  . Скорость есть первая производная по времени от смещения точки:
. Скорость есть первая производная по времени от смещения точки: 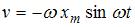 . Отсюда амплитудное значение скорости
. Отсюда амплитудное значение скорости  . Отсюда
. Отсюда  . Приведенные графики позволяют найти
. Приведенные графики позволяют найти  и
и  . Тогда циклическая частота колебаний точки
. Тогда циклическая частота колебаний точки  .
.
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Сложение гармонических колебаний
Сопротивление  катушка индуктивности
катушка индуктивности 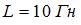 и конденсатор
и конденсатор  соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону
соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону  (В). Установите соответствие между сопротивлениями различных элементов цепи и их численными значениями.
(В). Установите соответствие между сопротивлениями различных элементов цепи и их численными значениями.
1. Активное сопротивление
2. Индуктивное сопротивление
3. Емкостное сопротивление

| 
| ||
| 
| ||

| 
| ||

| 
|
Решение:
Активное сопротивление  индуктивное сопротивление
индуктивное сопротивление  емкостное сопротивление
емкостное сопротивление 
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Энергия волны. Перенос энергии волной
Если в электромагнитной волне, распространяющейся в среде с показателем преломления 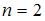 , значения напряженностей электрического и магнитного полей соответственно равны
, значения напряженностей электрического и магнитного полей соответственно равны  , то объемная плотность энергии составляет _____
, то объемная плотность энергии составляет _____ 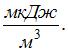
10 | 
|
Решение:
Плотность потока энергии электромагнитной волны (вектор Умова – Пойнтинга) равна:  . Также
. Также  где
где  объемная плотность энергии,
объемная плотность энергии,  скорость электромагнитной волны в среде,
скорость электромагнитной волны в среде,  скорость электромагнитной волны в вакууме,
скорость электромагнитной волны в вакууме, 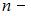 показатель преломления. Следовательно,
показатель преломления. Следовательно, 
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Волны. Уравнение волны
На рисунке представлен профиль поперечной упругой бегущей волны, распространяющейся со скоростью  . Циклическая частота волны равна …
. Циклическая частота волны равна …


| 
| 
| |

| 
| ||

| 
| ||

| 
|
Решение:
Волновое число  , где
, где 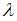 – длина волны, величину которой можно найти из графика:
– длина волны, величину которой можно найти из графика:  . Следовательно,
. Следовательно,  .
.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Энергия волны. Перенос энергии волной
На рисунке показана ориентация векторов напряженности электрического  и магнитного
и магнитного  полей в электромагнитной волне. Вектор Умова – Пойнтинга ориентирован в направлении …
полей в электромагнитной волне. Вектор Умова – Пойнтинга ориентирован в направлении …

3 | 
|
Решение:
Вектор Умова – Пойнтинга (вектор плотности потока энергии электромагнитного поля) равен векторному произведению:  , где
, где 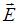 и
и  – векторы напряженностей электрического и магнитного полей электромагнитной волны соответственно. Векторы
– векторы напряженностей электрического и магнитного полей электромагнитной волны соответственно. Векторы 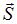 ,
, 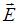 ,
,  образуют правую тройку векторов. Следовательно, вектор Умова – Пойнтинга ориентирован в направлении 3.
образуют правую тройку векторов. Следовательно, вектор Умова – Пойнтинга ориентирован в направлении 3.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Свободные и вынужденные колебания
Колебательный контур состоит из катушки индуктивности  конденсатора
конденсатора  и сопротивления
и сопротивления 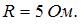 Добротность контура равна …
Добротность контура равна …
200 
|
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Сложение гармонических колебаний
Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными  и
и 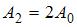 . Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания.
. Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания.
1. 0
2. 
3. 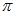

| 
| ||
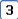
| 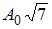
| ||

| 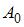
| ||

| 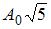
|
Решение:
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле  , где
, где  и
и 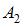 – амплитуды, (
– амплитуды, (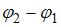 ) – разность фаз складываемых колебаний. Если разность фаз
) – разность фаз складываемых колебаний. Если разность фаз  ,
,  , то
, то 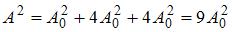 и
и  . Этот результат можно было получить сразу: при разности фаз
. Этот результат можно было получить сразу: при разности фаз  векторы
векторы  и
и 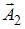 сонаправлены, и длина результирующего вектора
сонаправлены, и длина результирующего вектора 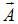 равна сумме длин складываемых векторов. Если
равна сумме длин складываемых векторов. Если 
 , то
, то  и
и  .
.
Если 
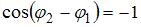 , то
, то  и
и 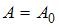 .
.






