ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Средняя энергия молекул
В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна:  . Здесь
. Здесь  , где
, где  ,
,  и
и  – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия (
– число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для гелия ( ) число i равно …
) число i равно …

| 
| ||

| |||

| |||

|
Решение:
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная  , а на каждую колебательную степень –
, а на каждую колебательную степень –  . Средняя кинетическая энергия молекулы равна:
. Средняя кинетическая энергия молекулы равна:  .
.
Здесь  – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:  , где
, где  – число степеней свободы поступательного движения, равное 3;
– число степеней свободы поступательного движения, равное 3;  – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;
– число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;  – число степеней свободы колебательного движения, минимальное количество которых равно 1.
– число степеней свободы колебательного движения, минимальное количество которых равно 1.
Для гелия ( ) (одноатомной молекулы)
) (одноатомной молекулы)  ,
, 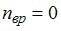 и
и  . Следовательно,
. Следовательно,  .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Распределения Максвелла и Больцмана
На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 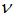 до
до  в расчете на единицу этого интервала.
в расчете на единицу этого интервала.

Для этих функций верными являются утверждения, что …

| 
| распределение 1 соответствует газу, имеющему наибольшую массу молекул | |

| 
| распределение 3 соответствует газу, имеющему наибольшую температуру | |

| распределение 1 соответствует газу, имеющему наименьшую массу молекул | ||

| распределение 3 соответствует газу, имеющему наименьшую температуру |
Решение:
Функция Максвелла имеет вид  .
.
Полная вероятность равна:  , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 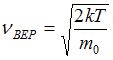 , при которой функция
, при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Второе начало термодинамики. Энтропия
При поступлении в неизолированную термодинамическую систему тепла в ходе обратимого процесса для приращения энтропии верным будет соотношение …

| 
| 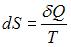
| |

| 
| ||

| 
| ||

| 
|
Решение:
Отношение  в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией
в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией  системы:
системы: 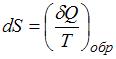 . В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах:
. В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах:  . Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса:
. Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса:  .
.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Первое начало термодинамики. Работа при изопроцессах
На рисунке представлена диаграмма циклического процесса идеального одноатомного газа:

За цикл газ получает количество теплоты (в  ), равное …
), равное …
33 | 
|
Решение:
Цикл состоит из изохорного нагревания (4–1), изобарного расширения (1–2), изохорного охлаждения (2–3) и изобарного сжатия (3–4). На первых двух этапах цикла газ получает теплоту. Согласно первому началу термодинамики, количество теплоты, получаемое газом, равно 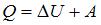 , где
, где  – изменение внутренней энергии,
– изменение внутренней энергии,  – работа газа. Тогда
– работа газа. Тогда  .
.

Таким образом, количество теплоты, получаемое газом за цикл, равно 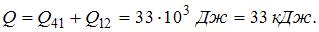
ЗАДАНИЕ N 21 сообщить об ошибке Тема: Первое начало термодинамики. Работа при изопроцессах Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна … 
|
5 | 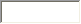
|
Решение:
Работу газа в циклическом процессе можно найти, определив площадь, ограниченную кривой цикла в координатах  Цикл имеет форму трапеции. Тогда
Цикл имеет форму трапеции. Тогда 
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Средняя энергия молекул
Средняя кинетическая энергия молекул газа при температуре  зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, отношение средней кинетической энергии колебательного движения к полной кинетической энергии молекулы азота (
зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, отношение средней кинетической энергии колебательного движения к полной кинетической энергии молекулы азота ( ) равно …
) равно …

| 
| 
| |

| 
| ||

| 
| ||

| 
|
Решение:
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная  , а на каждую колебательную степень –
, а на каждую колебательную степень –  Средняя кинетическая энергия молекулы равна:
Средняя кинетическая энергия молекулы равна:  . Здесь
. Здесь  – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:  , где
, где  – число степеней свободы поступательного движения, равное 3;
– число степеней свободы поступательного движения, равное 3;  – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;
– число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;  – число степеней свободы колебательного движения, минимальное количество которых равно 1.
– число степеней свободы колебательного движения, минимальное количество которых равно 1.
Для молекулярного азота (двухатомной молекулы)  ,
,  и
и  . Следовательно,
. Следовательно,  Полная средняя кинетическая энергия молекулы азота (
Полная средняя кинетическая энергия молекулы азота ( ) равна:
) равна:  , энергия колебательного движения
, энергия колебательного движения  , тогда отношение
, тогда отношение  .
.
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Распределения Максвелла и Больцмана
В трех одинаковых сосудах находится одинаковое количество газа, причем 

На рисунке представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 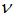 до
до  в расчете на единицу этого интервала.
в расчете на единицу этого интервала.

Для этих функций верными являются утверждения, что …

| 
| кривая 1 соответствует распределению по скоростям молекул газа при температуре 
| |

| 
| кривая 3 соответствует распределению по скоростям молекул газа при температуре 
| |

| кривая 2 соответствует распределению по скоростям молекул газа при температуре 
| ||

| кривая 3 соответствует распределению по скоростям молекул газа при температуре 
|
Решение:
Полная вероятность равна:  , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 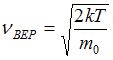 , при которой функция
, при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Второе начало термодинамики. Энтропия
В ходе необратимого процесса при поступлении в неизолированную термодинамическую систему тепла для приращения энтропии верным будет соотношение …

| 
| 
| |

| 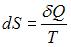
| ||

| 
| ||

| 
|
Решение:
Отношение  в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией
в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией  системы:
системы: 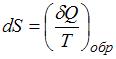 . В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах:
. В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах:  . Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса:
. Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса:  .
.
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Распределения Максвелла и Больцмана
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 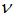 до
до  в расчете на единицу этого интервала.
в расчете на единицу этого интервала.

Если, не меняя температуры взять другой газ с меньшей молярной массой и таким же числом молекул, то …

| 
| максимум кривой сместится вправо в сторону больших скоростей | |

| 
| площадь под кривой не изменится | |

| высота максимума увеличится | ||

| площадь под кривой уменьшится |
Решение:
Функция Максвелла имеет вид  .
.
Полная вероятность равна:  , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры или массы молекул не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры или массы молекул не изменяется. Из формулы наиболее вероятной скорости 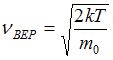 , при которой функция
, при которой функция  максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при уменьшении массы молекул газа максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при уменьшении массы молекул газа максимум функции сместится вправо, следовательно, высота максимума уменьшится.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Средняя энергия молекул
При комнатной температуре отношение  молярных теплоемкостей при постоянном давлении и постоянном объеме равно
молярных теплоемкостей при постоянном давлении и постоянном объеме равно  для …
для …

| 
| кислорода | |

| водяного пара | ||

| углекислого газа | ||

| гелия |
Решение:
Из отношения 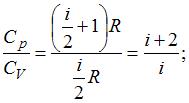
 найдем
найдем  ,
,  . Так как 3 поступательные и 2 вращательные степени свободы имеют двухатомные газы, следовательно, это кислород.
. Так как 3 поступательные и 2 вращательные степени свободы имеют двухатомные газы, следовательно, это кислород.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Второе начало термодинамики. Энтропия
На рисунке изображен цикл Карно в координатах (T, S), где S – энтропия. Адиабатное сжатие происходит на этапе …


| 
| 4 – 1 | |

| 2 – 3 | ||

| 1 – 2 | ||

| 3 – 4 |
Решение:
Адиабатные процессы происходят без теплообмена с окружающей средой, то есть система не получает тепла и не отдает его, 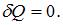 Изменение энтропии определяется как
Изменение энтропии определяется как  , следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном сжатии над газом совершают работу внешние силы, внутренняя энергия увеличивается:
, следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном сжатии над газом совершают работу внешние силы, внутренняя энергия увеличивается:  , температура газа увеличивается. Адиабатное сжатие происходит на этапе 4 – 1.
, температура газа увеличивается. Адиабатное сжатие происходит на этапе 4 – 1.
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Первое начало термодинамики. Работа при изопроцессах
На (P,V)-диаграмме изображены 2 циклических процесса.

Отношение работ  , совершенных в этих циклах, равно …
, совершенных в этих циклах, равно …
2 | 
|
Решение:
Работа газа в координатных осях  за цикл численно равна площади фигуры, ограниченной диаграммой кругового процесса. При осуществлении кругового процесса в прямом направлении (по часовой стрелке) работа газа за цикл положительна, так как при расширении газ совершает большую работу, чем затрачивается на его сжатие. Если круговой процесс осуществляется в обратном направлении (против часовой стрелки), то работа газа за цикл отрицательна. Работы газа в первом и втором циклах численно равны площадям прямоугольников:
за цикл численно равна площади фигуры, ограниченной диаграммой кругового процесса. При осуществлении кругового процесса в прямом направлении (по часовой стрелке) работа газа за цикл положительна, так как при расширении газ совершает большую работу, чем затрачивается на его сжатие. Если круговой процесс осуществляется в обратном направлении (против часовой стрелки), то работа газа за цикл отрицательна. Работы газа в первом и втором циклах численно равны площадям прямоугольников:  и
и  Отношение работ, совершенных в этих циклах:
Отношение работ, совершенных в этих циклах: 
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Первое начало термодинамики. Работа при изопроцессах
Один моль идеального одноатомного газа в ходе некоторого процесса получил  теплоты. При этом его температура понизилась на
теплоты. При этом его температура понизилась на  . Работа (
. Работа (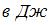 ), совершенная газом, равна …
), совершенная газом, равна … 






