Тема: Динамика поступательного движения 1 страница

МЕХАНИКА

ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Работа. Энергия
Частица совершила перемещение по некоторой траектории из точки 1 с радиус-вектором в точку 2 с радиус-вектором . При этом на нее действовала сила (радиус-векторы , и сила заданы в единицах СИ). Работа, совершенная силой , равна …

26 |

 

Решение:
По определению . С учетом того, что ,

 

ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Элементы специальной теории относительности
Релятивистское сокращение длины ракеты составляет 20%. При этом скорость ракеты равна …

			0,6 с
			0,8 с
			0,2 с
			0,4 с

 

Решение:
Движение макроскопических тел со скоростями, соизмеримыми со скоростью света в вакууме, изучается релятивистской механикой. Одним из следствий преобразований Лоренца является так называемое Лоренцево сокращение длины, состоящее в том, что линейные размеры тела сокращаются в направлении движения: . Здесь 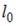– длина тела в системе отсчета, относительно которой тело неподвижно; 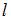– длина тела в системе отсчета, относительно которой тело движется со скоростью . При этом поперечные размеры тела не изменяются. По условию релятивистское сокращение длины ракеты . . Отсюда скорость ракеты .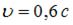

 

ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Кинематика поступательного и вращательного движения
Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике.

Угловое перемещение (в радианах) в промежутке времени от 2 с до 4 с равно …

 

Решение:
По определению . Отсюда и . Используя геометрический смысл интеграла, искомое угловое перемещение можно найти как площадь трапеции: 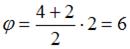рад.

 

ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Динамика поступательного движения
Вдоль оси OX навстречу друг другу движутся две частицы с массами m₁ = 4 г и m₂ = 2 г и скоростями V₁ = 5 м/с и V₂ = 4 м/с соответственно. Проекция скорости центра масс на ось ОХ (в единицах СИ) равна …

2 |

 

Решение:
Скорость центра масс механической системы равна отношению импульса системы к ее массе: . Для рассматриваемой системы из двух частиц . Проекция скорости центра масс на ось ОХ

 

ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Законы сохранения в механике
Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки с одной и той же высоты. Если трением и сопротивлением воздуха можно пренебречь, то отношение скоростей 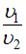, которые будут иметь эти тела у основания горки, равно …

 

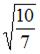
Решение:
В рассматриваемой системе «тело – Земля» действуют только консервативные силы, поэтому в ней выполняется закон сохранения механической энергии, согласно которому , или 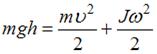, где J – момент инерции тела относительно оси, проходящей через центр масс, 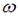– угловая скорость вращения вокруг этой оси, h – высота, с которой скатывается тело. Отсюда с учетом того, что , получаем: . Отсюда . Моменты инерции сплошного и полого цилиндров равны соответственно: и 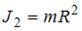. Тогда искомое отношение скоростей .

 

ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Динамика вращательного движения
Если ось вращения тонкостенного кругового цилиндра перенести из центра масс на образующую (рис.), то момент инерции относительно новой оси _____ раза.

			увеличится в 2
			уменьшится в 2
			увеличится в 1,5
			уменьшится в 1,5

 

Решение:
Момент инерции тонкостенного кругового цилиндра массы m и радиуса R относительно оси, проходящей через центр масс, вычисляется по формуле . Момент инерции относительно оси, проходящей через образующую, найдем по теореме Штейнера: . Тогда , то есть момент инерции увеличится в 2 раза.

ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Элементы специальной теории относительности
-мезон, двигавшийся со скоростью (с – скорость света в вакууме) в лабораторной системе отсчета, распадается на два фотона: g₁ и g₂. В системе отсчета мезона фотон g₁ был испущен вперед, а фотон g₂ – назад относительно направления полета мезона. Скорость фотона g₂ в лабораторной системе отсчета равна …

 

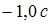
Решение:
Фотон является частицей, которая может существовать, только двигаясь со скоростью с, то есть со скоростью света в вакууме. Кроме того, согласно одному из постулатов специальной теории относительности – принципу постоянства скорости света, скорость света в вакууме не зависит от движения источника света и, следовательно, одинакова во всех инерциальных системах отсчета. Поэтому скорость фотона g₂ с учетом направления его движения в лабораторной системе отсчета равна: .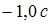

 

ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Работа. Энергия
Потенциальная энергия частицы задается функцией .
-компонента (в Н) вектора силы, действующей на частицу в точке А (3, 1, 2), равна …
(Функция 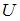и координаты точки А заданы в единицах СИ.)

36 |

 

Решение:
Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид , или , , . Таким образом,

 

ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Динамика вращательного движения
Направления векторов момента импульса и момента силы для равнозамедленного вращения твердого тела правильно показаны на рисунке …

 

Решение:
Момент силы определяется соотношением 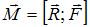, где – радиус-вектор точки приложения силы. Направление вектора момента силы можно определить по правилу векторного произведения или по правилу правого винта (буравчика). Таким образом, момент силы направлен вдоль оси вращения. Согласно основному закону динамики вращательного движения твердого тела, , где момент инерции тела, вектор углового ускорения, который сонаправлен с вектором момента силы. Момент импульса равен , где вектор угловой скорости, который по правилу правого винта направлен вдоль оси вращения, следовательно, и вектор момента импульса направлен так же. Поскольку вращение равнозамедленное, вектор углового ускорения направлен противоположно вектору угловой скорости, значит, векторы и противоположны. Условию задачи соответствует рисунок 3.

 

ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Кинематика поступательного и вращательного движения
Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике.

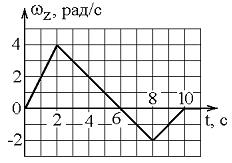
Угловое перемещение (в радианах) в промежутке времени от 2 с до 4 с равно …

 

Решение:
По определению . Отсюда и . Используя геометрический смысл интеграла, искомое угловое перемещение можно найти как площадь трапеции: рад.

 

ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Законы сохранения в механике
Сплошной цилиндр и шар, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми скоростями на горку. Если трением и сопротивлением воздуха можно пренебречь, то отношение высот , на которые смогут подняться эти тела, равно …

 

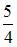
Решение:
В рассматриваемой системе «тело – Земля» действуют только консервативные силы, поэтому в ней выполняется закон сохранения механической энергии, согласно которому , или , где J – момент инерции тела относительно оси, проходящей через центр масс, 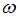– угловая скорость вращения вокруг этой оси, h – высота, на которую сможет подняться тело. Отсюда с учетом того, что , получаем: 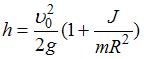. Моменты инерции сплошного цилиндра и шара равны соответственно и . Тогда искомое отношение высот .

 

ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Динамика поступательного движения
Импульс материальной точки изменяется по закону (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 4 c, равен …

26 |

 

Решение:
Согласно второму закону Ньютона скорость изменения импульса материальной точки равна действующей на нее силе: . Тогда зависимость силы от времени имеет вид . Модуль силы , и в момент времени t = 4 c

ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Динамика вращательного движения
Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил (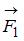, , 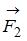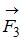или 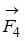), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение …

			,

 

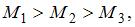
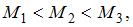
Решение:
При вращении тела вокруг неподвижной оси момент относительно этой оси создает только одна составляющая действующей на него силы, а именно касательная к траектории точки ее приложения 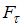. Тогда момент силы относительно неподвижной оси равен: 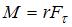, где r – радиус-вектор точки приложения силы. В данном случае составляющая 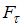одинакова для трех сил: 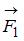, 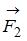и 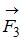, а для силы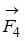 . Кроме того, все силы приложены в одной точке. Поэтому , .

 

ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Элементы специальной теории относительности
Космический корабль летит со скоростью 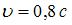( скорость света в вакууме) в системе отсчета, связанной с некоторой планетой. Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное направлению движения. Длина этого стержня с точки зрения другого космонавта …

			равна 1,0 м при любой его ориентации
			изменяется от 1,0 м в положении 1 до 1,67 м в положении 2
			изменяется от 1,0 м в положении 1 до 0,6 м в положении 2
			изменяется от 0,6 м в положении 1 до 1,0 м в положении 2