Мета: Ввести поняття репера на проективній площині, прямій; обґрунтувати властивості проективних координат точок на прямій, площині; навчитися будувати точки на проективній прямій і площині відносно різних реперів (які містять або не містять невласні точки).
План
1. Репер на проективній площині, на проективній прямій. Властивості репера
2. Координати точки на проективній площині, на проективній прямій.
3. Умова належності трьох точок прямій на площині.
4. Проекція точки на сторони координатного трикутника.
Ключові слова: точки загального положення, упорядкована четвірка точок, репер, координатний трикутник, погоджені вектори, координати точки, умова належності трьох точок прямій, проекції точки на сторони координатного трикутника.
РЕПЕР НА ПРОЕКТИВНІЙ ПЛОЩИНІ

 P2 V3/
P2 V3/
A, B, C, D Î P2
Означення: Упорядковану четвірку точок загального положення на проективній площині називають проективним репером R = (A,В,С, D)
інакше R = (A1, A2, A3, E)
 А2 Одинична точка
А2 Одинична точка
E
A1 A3
вершини координатного координатний трикутник
трикутника
Нехай R = (A1, A2, A3, E)




 1
1  1 ,
1 ,  2
2  2,
2,  3
3  3,
3, 
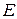
Якщо  1 +
1 +  2 +
2 +  3 =
3 =  , то
, то  1,
1,  2,
2,  3 - погодженн і
3 - погодженн і
1. Теорема Для " R =(A1, A2, A3, E), $  1,
1,  2,
2,  3,
3,  ê
ê  1+
1+  2+
2+  3=
3= 

 ● A1
● A1  1 RÌ P2 V3/
1 RÌ P2 V3/
 A2
A2  2
2

 A3
A3  3
3

 E
E 

 1,
1,  2,
2,  3,
3,  Î V3/ Þ
Î V3/ Þ  1,
1,  2,
2,  3,
3,  – л.з.
– л.з.

 = λ 1
= λ 1  1+ λ 2
1+ λ 2  2+ λ3
2+ λ3  3
3

 позначимо
позначимо

 1
1  2
2  3
3


 ,
,  1,
1,  2,
2,  3 – погоджені і визначають репер R ●
3 – погоджені і визначають репер R ●
 Зауваження: Якщо μ
Зауваження: Якщо μ  = μ
= μ  1+ μ
1+ μ  2+ μ
2+ μ  3
3

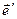 =
=  1+
1+  2+
2+  3 Þ
3 Þ 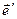 ,
,  1,
1,  2,
2,  3 - погоджені
3 - погоджені
 $ безліч систем погоджених векторів відносно R.
$ безліч систем погоджених векторів відносно R.
2. Теорема Якщо кожна з систем векторів  1,
1,  2,
2,  3,
3,  і
і  1 ,
1 ,  2,
2,  3,
3,  погоджена відносно R=(A1,A2, A3, E,) то $ λ¹0
погоджена відносно R=(A1,A2, A3, E,) то $ λ¹0
таке, що  i = λ
i = λ  і (i = 1,2,3)
і (i = 1,2,3)  = λ
= λ 
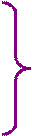
 ● За умовою
● За умовою 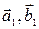 A1
A1  1 = λ1
1 = λ1  1
1


 A2
A2  2 = λ2
2 = λ2  2
2

 A3
A3  3 = λ3
3 = λ3  3
3

 E
E 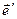 = λn
= λn 










 єдиність розкладу!
єдиність розкладу!
 |



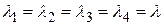
ОТЖЕ
 ● ●
|

 Аналогічно. Репер на прямій--- Три точки
Аналогічно. Репер на прямій--- Три точки 


 A1
A1  1 A2
1 A2  2 E
2 E 
Якщо  , то
, то  -погоджені
-погоджені
КООРДИНАТИ ТОЧКИ НА ПРОЕКТИВНІЙ ПЛОЩИНІ
 Р2 V3΄
Р2 V3΄
 R=(A1,A2,A3,E)
R=(A1,A2,A3,E)  P2
P2  – базис V3΄
– базис V3΄

 X
X 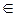 P2
P2 
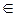 V3΄
V3΄

 (х1, х2, х3) координати
(х1, х2, х3) координати 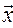 в базисі
в базисі 
 (х1, х2, х3) координати точки Х в репері R
(х1, х2, х3) координати точки Х в репері R

Означення Координати точки - це координати вектора, який її породжує.
Оскільки, то всі координати точки не можуть дорівнювати 0.
ВЛАСТИВОСТІ КООРДИНАТ ТОЧКИ
● X 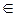 P2, R
P2, R  P2 R=(A1,A2, A3, E,)
P2 R=(A1,A2, A3, E,)
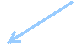




 R
R  (1)
(1)





 (х1, х2, х3)
(х1, х2, х3)  (2)
(2)

 X
X 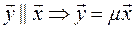 (3)
(3)

 (y1, y2, y3)
(y1, y2, y3)  (4)
(4)
 (4)
(4)  (3), (1), (2)
(3), (1), (2) 
 . (5)
. (5)
.



 Отже, проективні координати точки відносно заданого
Отже, проективні координати точки відносно заданого
репера визначаються з точністю до сталого множника. ●
 Зауваження 1) R=(A1,A2,A3,E): A1 (1,0,0)
Зауваження 1) R=(A1,A2,A3,E): A1 (1,0,0) 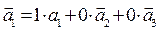


 A2 (0,1,0)
A2 (0,1,0)  .?....... A3 (0,0,1)
.?....... A3 (0,0,1)  .?......., E(1,1,1)
.?......., E(1,1,1) 
Зауваження 2) Координати точки на прямій
 R=(A1,A2,E)
R=(A1,A2,E)  d V2΄,
d V2΄,  – базис V2΄
– базис V2΄
 Якщо X
Якщо X 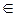 d, то
d, то 
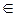 V2΄,
V2΄, 
(х1, х2) – координати точки Х в репері R на прямій.
Тоді A1 (1,0); A2 (0,1); Е (1,1) ----- R
Умова належності трьох точок прямій на площині
●  Р2 V3 ΄,
Р2 V3 ΄,  – базис V3΄
– базис V3΄
R  P2, X, Y, Z
P2, X, Y, Z 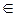 P2
P2


 X (х1, х2, х3) X
X (х1, х2, х3) X  ((х1, х2, х3)
((х1, х2, х3)
 Y (y1, y2, y3) R Y
Y (y1, y2, y3) R Y  (y1, y2, y3)
(y1, y2, y3) 
 Z (z1, z2, z3) Z
Z (z1, z2, z3) Z  (z1, z2, z3)
(z1, z2, z3)
Якщо X, Y, Z 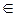 d
d 






Отже, якщо три точки належать прямій, то....●
ПРОЕКЦІЇ ТОЧКИ НА СТОРОНИ КООРДИНАТНОГО ТРИКУТНИКА.
 Р2 V3΄
Р2 V3΄
|

|
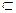 P2
P2  ,
,
|
|
|

|
|
|
 Проекції точки Е на сторони координатного
Проекції точки Е на сторони координатного
трикутника з центрів A1, A2, A3 E1 (?), E2 (?), E3 (?)
 ● Нехай E1 (y1, y2, y3) R
● Нехай E1 (y1, y2, y3) R

 E1
E1 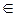 A1E
A1E  y2 = y3
y2 = y3
 E1
E1 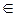 A2A3
A2A3  y1 = 0 E1(0, y2, y2)= E1(0, 1,1)
y1 = 0 E1(0, y2, y2)= E1(0, 1,1)
Аналогічно E2 (1,0,1) R1= (A1,A3,E2) – репер на A1,A3
E3 (1 1,0) R3= (A1,A2,E3) – репер на A1,A2 ●
Оскільки:
 A2
A2  (0,1,0)
(0,1,0)


 A3
A3  (0,0,1) звідки
(0,0,1) звідки 
 E1
E1  (0,1,1)
(0,1,1)
R1= (A2,A3,E1) – репер на A2A3
Аналогічно..........
● 


 Нехай M (х1, х2, х3) R, а M2 проекція точки M на A1A3 M2 (?,?,?)
Нехай M (х1, х2, х3) R, а M2 проекція точки M на A1A3 M2 (?,?,?)
Нехай M2 (y1, y2, y3) - R

 1) M2
1) M2 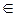 A1A3
A1A3 

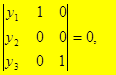 y2=0 2) M2
y2=0 2) M2 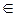 A2M
A2M 
 y1x3 - x1y3 =0
y1x3 - x1y3 =0




 M2 (
M2 ( ) = M2 (
) = M2 ( )
)

 Отже, M1 (
Отже, M1 ( ) M1 (
) M1 ( ) R1= (A2,A3,E1)
) R1= (A2,A3,E1)

 M2 (
M2 (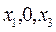 ) R M2 (
) R M2 ( ) R2= (A1,A3,E2)
) R2= (A1,A3,E2)
 M3 (
M3 (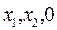 ) M3 (
) M3 ( ) R3= (A1,A2,E3)
) R3= (A1,A2,E3)

 М= A1 M1
М= A1 M1  A2 M2
A2 M2  A3 M3. ●
A3 M3. ●
Питання для самоперевірки.
1. Що називається репером на проективній площині?
2. Як позначається репер?
3. Якщо R=(A1, A2, A3, E)-- репер на площині,то як називаються точки A1, A2, A3, E?
4. Які вектори породжують точки A1, A2, A3, E?
5. Які вектори називаються погодженими відносно даного репера?
6. Сформулювати теорему про систему погоджених векторів відносно заданого репера.
7. Скільки існує систем погодження векторів відносно заданого репера?
8. Як відрізняються одна від одної системи погоджених векторів?
9. Що називають координатами точки на проективній площині?
10. Які властивості мають координати точки?
11. Що можна сказати про координати точок, які належать сторонам координатного трикутника?
12. Які координати мають вершини координатного трикутника?
13. Що можна сказати про точки (1;-2;3) і (2;-4;6), задані своїми координатами відносно деякого репера R?
14. Що таке репер на прямій?
15. Скільки координат має точка на прямій?
16. Чи існує на проективній площині точки, всі координати яких рівні нулю?
17. Яка умова належності трьох точок прямій та площині?
18. Як позначаються проекції точки Е з вершин координатного трикутника на його сторони?
19. Які координати мають проекції точки М(х1, х2, х3) на сторони координатного трикутника даного репера відносно цього репера і відносно реперів на його сторонах?
20. Доповнити запис М= A1 M1  A2......
A2......






