Изменение начала координат и поворот осей

ПП 7.3. Преобразования координат

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

Преобразования координат

 

Параллельный перенос

Перенесём начало координат из точки О в точку О ₁ параллельным переносом осей. Пусть в системе ко­ординат xoy точка М имеет координаты x и y. Система координат x ¢ O ₁ y ¢ получена из системы координат xOy параллельным переносом осей, при котором начало координат О ₁ имеет координаты x ₀ и y ₀ в системе координат xOy. Точка М в системе координат x ¢ O ₁ y ¢ имеет координаты x ¢ и y ¢. Связь между координатами точки M (x, y) и точки M (x ¢, y ¢) в старой и новой системах координат задается формулами:

(1)

(2)

Уравнения кривых второго порядка, когда их центры симметрии находятся в точке с координатами O ₁(x ₀, y ₀), получаются с помощью преобразования координат при параллельном переносе осей (2).

- уравнение окружности с центром в точке O ₁(x ₀, y ₀) и радиусом R.

Аналогично получаются уравнения других кривых второго порядка:

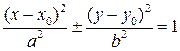- уравнения эллипса и гиперболы с цен­тром симметрии в точке O ₁(x ₀, y ₀);

- уравнение параболы с вершиной в точке O ₁(x ₀, y ₀).

При этом, например, уравнения директрис эллипса и гиперболы: , а параболы: . Аналогично преобразуются и уравнения асимптот гиперболы: .

Поворот координатных осей

Выведем формулу преобразования координат при повороте координатных осей.

Повернём оси координат на угол a относительно исходной системы координат. Координаты точки М в системе координат x ¢ Oy ¢ равны x ¢ и y ¢. Найдём её координаты в системе координат xOy. В треугольнике CMD 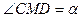, OD = x ¢, MD = y ¢.

Следовательно,

x = OA = OB – AB = OB - CD, y = MA = AC + CM = DB + CM.

Поскольку

то

(3)

Эти формулы выражают старые координаты (x, y) произвольной точки М через новые координаты (x ¢, y ¢) этой же точки при повороте осей на угол a.

Формулы, выражающие новые координаты (x ¢, y ¢) точки М через её старые координаты (x, y), получим из следующих соображений: если новая система получена поворотом старой на угол a, то старая система получается поворотом новой на угол (- a), поэтому в равенствах (3) можно поменять местами старые и новые координаты, заменяя одновременно a на (- a).

Выполнив это преобразование, получим

При этом, например, уравнения директрис эллипса (ги­перболы) и параболы принимают вид:

Изменение начала координат и поворот осей

Если оси декартовой прямоугольной системы переносятся параллельно на величины x ₀ по оси ox и на y ₀ по оси oy и, кроме того, поворачиваются на угол a, то этому изменению системы соответствуют формулы преобразования координат, выражающие старые координаты через новые:

(4)

и новые координаты через старые:

(5)