Тема1: Поняття проективного простору.
Мета: сформувати поняття проективного простору; з’ясувати суть його властивостей.
План
1. З історії виникнення проективної геометрії.
2. Поняття проективного простору.
3. Властивості проективного простору.
Ключові слова: п+1 вимірний векторний простір, n -вимірний проективний простір, вектор породжує точку, проективна площина, проективна пряма, трьохвимірний проективний простір.
(З історії виникнення проективної геометрії ---- див 2, ст.5-8, 341)
Поняття проективного простору
Vn+1 – n+1 вимірний векторний простір над полем R дійсних чисел.
V/ = Vn+1\{  } " Р≠Ø
} " Р≠Ø
Означення: Множина Р називається n-вимірним проективним простором, якщо визначено відображення f: V/→Р, яке задовольняє властивостям:
1) f – сюр’єктивне
 2)
2) 
 Елементи множини Р називають точками. Запис
Елементи множини Р називають точками. Запис  читається: вектор
читається: вектор  породжує точку X. (будемо використовувати позначення
породжує точку X. (будемо використовувати позначення  )
)
Тоді друга властивість в означенні читається так: колінеарні вектори породжують одну і ту ж точку проективного простору
За означенням
V4/ породжує Р3 (3-х вимірний проективний простір)
V3/ породжує Р2 (проективну площину)
V2/ породжує Р1 (проективну пряму)
V1/ породжує Р0 (точк у)
Зауваження: Так як V4/ (V3/, V2/) містять нескінченну множину не колінеарних векторів, то проективний простір, проективна площина, проективна пряма містять нескінченну множину точок.
Властивості проективного простору
1. У 3-х вимірному проективному просторі існують 4 точки, які не лежать в одній площині. На проективній площині існують 3 точки, які не лежать на одній прямій.

 ● Р3 V4/, (
● Р3 V4/, (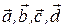 ) — базис V4/
) — базис V4/


 A, B, C, D
A, B, C, D
 | |||
 | |||
не можуть лежати в

 одній площині Р2 V3/
одній площині Р2 V3/
Якщо припустити, що A,B,C,D є Р2
 то
то 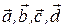 є V3/
є V3/

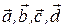 – л.з., що суперечить
– л.з., що суперечить
Аналогічно: існують A,B,C Ï d
(самостійно)●
2. Через будь-які дві точки проходить одна і тільки одна пряма
●  Дано: Точки A і B, А≠В
Дано: Точки A і B, А≠В


 Відомо: А
Відомо: А  , В
, В  ,
, 

Розглянемо: ( ,
,  ) – базис V2/ (1)
) – базис V2/ (1)
 За означенням: V2/ AB – пряму
За означенням: V2/ AB – пряму
Доведемо, що AB= d — єдина пряма
Припустимо $ d/ ½ A, B Î d/
 Нехай d/ W2/
Нехай d/ W2/
З того, що A, B Î d/ Þ  ,
,  є W2/ Þ (
є W2/ Þ ( ,
,  ) базис W2/ (2)
) базис W2/ (2)
 (1), (2) Þ V2/= W2/
(1), (2) Þ V2/= W2/
 d = d/
d = d/
AB єдина пряма, яка проходить через точки A і B ●
3. Через будь-які три точки, що не лежать на одній прямій, проходить одна і тільки одна площина (Самостійно)
4. Якщо дві точки А і В лежать у площині Р2 то і пряма АВ лежить у цій площині (тобто кожна точка прямої АВ лежить у площині Р2)
 ● Нехай А і В є Р2 V3/
● Нехай А і В є Р2 V3/



 А
А 
 (
( ,
,  ) базис V2/
) базис V2/


 А≠В,
А≠В, 

 V2
V2 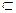 V3/
V3/
 В
В 
 є V3/
є V3/

 V2/ V3/
V2/ V3/
 AB P2
AB P2
 |
AB Ì P2

 " M є AB Þ
" M є AB Þ  = λ
= λ  +μ
+μ  1 Þ
1 Þ  Î V2/ Ì V3/
Î V2/ Ì V3/
M Î P2 ●
5. Будь-які дві прямі на проективній площині завжди перетинаються.
● P2 – проективна площина

d1, d2 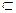 P2
P2
 P2 V/3
P2 V/3

 V2/, W2/ Ì V3/ Правило
V2/, W2/ Ì V3/ Правило
 Vm, Wk Ì Vn Vm+Wk=Vn+ Vp
Vm, Wk Ì Vn Vm+Wk=Vn+ Vp
 2+2=3+1 Vp-простір перерізу Vm, Wk
2+2=3+1 Vp-простір перерізу Vm, Wk
 V1/ - простір перерізу просторів V2/ і W2/ у V3/
V1/ - простір перерізу просторів V2/ і W2/ у V3/
Векторний простір V1/ - це множина

 колінеарних між собоюненульових векторів V1/ M0
колінеарних між собоюненульових векторів V1/ M0
Отже, d1 Ç d1 = M0 ●
6. Будь-які дві площини у трьохвимірному просторі завжди перетинаються
 ●
●
V3/, W3/ Ì V4/
 3+3=4+2
3+3=4+2

Vπ/= V2 простір перерізу
Отже, P2 Ç P2/ = Р1 ●
7. Будь-яка площина і пряма, яка їй не належить, у трьохвимірному просторі завжди перетинаються (Самостійно)
Питання для самоперевірки.
1. Сформулювати означення n-вимірного проективного простору.
2. Як називаються елементи множини Р?
3. Як прочитати запис:  ?
?
4. Що,за означенням, породжують векторні простори  ?
?
5. Як можна сформулювати другу властивість в означенні проективного простору?
6. Сформулювати властивості проективного простору?
7. Чи є паралельні прямі на проективній площині?
8. Яку точку породжує нульовий вектор?
9. Яке співвідношення між розмірністю проективного простору і векторного, який його породжує?
10 Що можна сказати про взаємне розміщення двох проективних площин, прямої і площини у просторі?






