Прямые y 1= k 1 x + b 1 и y 2= k 2 x + b 2 параллельны друг другу, если 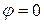 . Следовательно,
. Следовательно,  , то есть k 1= k 2.
, то есть k 1= k 2.
Прямые y 1= k 1x+ b 1 и y 2= k 2 x + b 2 перпендикулярны друг другу, если  . Следовательно,
. Следовательно, 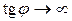 , то есть k 1 k 2 = -1. Отсюда
, то есть k 1 k 2 = -1. Отсюда  .
.
Если прямые заданы общими уравнениями, то:
А 1 В 1 – А 2 В 1=0, 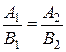 – условие параллельности,
– условие параллельности,
А 1 А 2+ В 1 В 2=0 – условие перпендикулярности прямых.
Уравнение пучка прямых
Совокупность всех прямых плоскости, проходящих через некоторую точку M (x 0 ,y 0), называется пучком прямых с центром М 0.
Если A 1 x+B 1 y+C 1=0 и A 2 x+B 2 y+C 2=0 - уравнения двух прямых, пересекающихся в точке М 0; то уравнение A 1 x+B 1 y+C 1+ 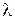 (A 2 x+B 2 y+C 2)=0
(A 2 x+B 2 y+C 2)=0
определяет все прямые пучка, кроме второй из прямых.
| ПП 7.1. Прямая на плоскости | ||
| ПП 7.1. №1. | треугольник задан уравнениями трех его сторон:
АС: х – 2 у + 5 = 0,
АВ: х + 2 у – 3 = 0,
ВС: 2 х + у – 15 = 0.
Определите следующие элементы треугольника:
а) координаты вершин,
б) уравнения высот,
в) уравнения медиан,
г) длины сторон,
д) уравнения биссектрис,
ж) центр и радиус вписанной окружности,
з) центр и радиус описанной окружности,
и) центр тяжести треугольника,
к) внутренние углы треугольника,
л) площадь треугольника.
Решение:
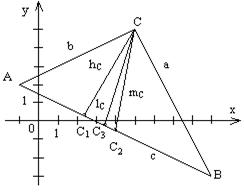 а) Координаты вершин треугольника находятся как точки пересечения соответствующих сторон. Так, например, координаты точки А являются решением системы уравнений
а) Координаты вершин треугольника находятся как точки пересечения соответствующих сторон. Так, например, координаты точки А являются решением системы уравнений
 А (-1, 2).
Аналогично находятся
В (9, -3) и С (5, 5).
б) Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону.
Так h c = CC 1 ^ AB. Уравнение высоты СС 1 ищем как уравнение прямой у = k 1 x + b, если известен угловой коэффициент прямой АВ: А (-1, 2).
Аналогично находятся
В (9, -3) и С (5, 5).
б) Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону.
Так h c = CC 1 ^ AB. Уравнение высоты СС 1 ищем как уравнение прямой у = k 1 x + b, если известен угловой коэффициент прямой АВ:  равный равный  Из условия перпендикулярности прямых
k 1 k 2=-1 ® k 1 = 2. Поскольку высота СС 1 проходит через точку (5, 5), уравнение h c имеет вид: у – 5 = 2 × (х – 5) или у = 2 х – 5.
Анализ уравнений сторон АС:
Из условия перпендикулярности прямых
k 1 k 2=-1 ® k 1 = 2. Поскольку высота СС 1 проходит через точку (5, 5), уравнение h c имеет вид: у – 5 = 2 × (х – 5) или у = 2 х – 5.
Анализ уравнений сторон АС: 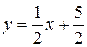 и ВС: у = -2 х + 5 убеждает нас в том, что АС ^ ВС, и треугольник является прямоугольным, значит, уравнение h A: и ВС: у = -2 х + 5 убеждает нас в том, что АС ^ ВС, и треугольник является прямоугольным, значит, уравнение h A:  h B: у = -2 х + 15.
в) Медианой называется отрезок прямой, соединяющей вершину треугольника с серединой противолежащей стороны.
Координаты середин сторон находятся по формулам деления отрезка в данном отношении: С 2(4, -1/ 2), В 2 (2, 7/2), А 2 (7, 1).
Уравнение медианы mC = CC 2 получается как уравнение прямой, проходящей через точки С и С 2: h B: у = -2 х + 15.
в) Медианой называется отрезок прямой, соединяющей вершину треугольника с серединой противолежащей стороны.
Координаты середин сторон находятся по формулам деления отрезка в данном отношении: С 2(4, -1/ 2), В 2 (2, 7/2), А 2 (7, 1).
Уравнение медианы mC = CC 2 получается как уравнение прямой, проходящей через точки С и С 2:
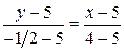 или mC:11 х– 2 у– 45 = 0.
Аналогично mВ:13 х+ 14 у– 75 = 0,
mА: x+ 8 y– 15 = 0.
г) Длины сторон найдем по формуле расстояния между двумя точками: или mC:11 х– 2 у– 45 = 0.
Аналогично mВ:13 х+ 14 у– 75 = 0,
mА: x+ 8 y– 15 = 0.
г) Длины сторон найдем по формуле расстояния между двумя точками:
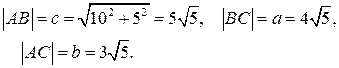 д) Биссектрисой треугольника называется лежащий в треугольнике отрезок прямой, которая делит его внутренний угол пополам.
Укажем два способа нахождения уравнения биссектрисы треугольника.
1). Биссектриса делит противолежащую сторону в отношении, пропорциональном прилежащим сторонам.
Если С3 – точка пересечения биссектрисы lC = CC3 со стороной АС, то
д) Биссектрисой треугольника называется лежащий в треугольнике отрезок прямой, которая делит его внутренний угол пополам.
Укажем два способа нахождения уравнения биссектрисы треугольника.
1). Биссектриса делит противолежащую сторону в отношении, пропорциональном прилежащим сторонам.
Если С3 – точка пересечения биссектрисы lC = CC3 со стороной АС, то
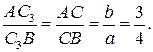 Координаты точки С3 находим по формулам деления отрезка в данном отношении l = 3/4: С 3 (23/7, -1/7).
Уравнение биссектрисы lC = CC3 получается как уравнение прямой, проходящей через точки С3 и С (5, 5):
Координаты точки С3 находим по формулам деления отрезка в данном отношении l = 3/4: С 3 (23/7, -1/7).
Уравнение биссектрисы lC = CC3 получается как уравнение прямой, проходящей через точки С3 и С (5, 5):
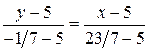 или 3 х – у – 10 = 0.
2). Уравнение биссектрисы lC = CC3 может быть найдено из условия того, что точки биссектрисы CC3 равноудалены от сторон АС и СВ.
Вычислим отклонения точки (х, у), лежащей на биссектрисе, от сторон АС и СВ (см. п.2.7): или 3 х – у – 10 = 0.
2). Уравнение биссектрисы lC = CC3 может быть найдено из условия того, что точки биссектрисы CC3 равноудалены от сторон АС и СВ.
Вычислим отклонения точки (х, у), лежащей на биссектрисе, от сторон АС и СВ (см. п.2.7):
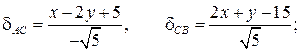 dАС и dСВ отрицательны, так как начало координат и точки биссектрисы треугольника лежат по одну сторону от каждой из сторон АС и СВ. Учитывая, что d = |d|, уравнение биссектрисы получим из равенства
dАС и dСВ отрицательны, так как начало координат и точки биссектрисы треугольника лежат по одну сторону от каждой из сторон АС и СВ. Учитывая, что d = |d|, уравнение биссектрисы получим из равенства 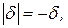  ,-dАС = -dСВ, которое принимает вид: ,-dАС = -dСВ, которое принимает вид:  или lC: 3 х – у – 10 = 0.
Для вычисления биссектрисы угла А lА применим второй способ.
Отклонение
или lC: 3 х – у – 10 = 0.
Для вычисления биссектрисы угла А lА применим второй способ.
Отклонение  отрицательно, так как начало координат и биссектриса lА лежат по одну сторону от стороны АС.
Отклонение отрицательно, так как начало координат и биссектриса lА лежат по одну сторону от стороны АС.
Отклонение 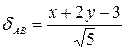 положительно, так как начало координат и биссектриса lА лежат по разные стороны от стороны АВ.
Для биссектрисы lА справедливо -dАС = dАВ,
то есть положительно, так как начало координат и биссектриса lА лежат по разные стороны от стороны АВ.
Для биссектрисы lА справедливо -dАС = dАВ,
то есть  или х – 2 у + 5 = х + 2 у – 3.
Следовательно, 4 у = 8. Таким образом, lА: у = 2.
уравнение lВ: х+у – 6 = 0 может быть найдено одним из двух способов.
ж) Центр вписанной окружности находится в точке пересечения биссектрис lС и lА треугольника. или х – 2 у + 5 = х + 2 у – 3.
Следовательно, 4 у = 8. Таким образом, lА: у = 2.
уравнение lВ: х+у – 6 = 0 может быть найдено одним из двух способов.
ж) Центр вписанной окружности находится в точке пересечения биссектрис lС и lА треугольника.
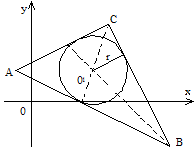 Система уравнений, составленная из уравнений биссектрис:
Система уравнений, составленная из уравнений биссектрис:
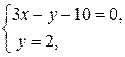 имеет решение х = 4, у = 2.
Следовательно, центр вписанной окружности находится в точке О 1 (4, 2).
Радиус вписанной окружности найдем как расстояние от точки О 1 до стороны АС:
имеет решение х = 4, у = 2.
Следовательно, центр вписанной окружности находится в точке О 1 (4, 2).
Радиус вписанной окружности найдем как расстояние от точки О 1 до стороны АС: 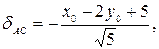 где х 0 = 4, у 0 = 2.
Таким образом, где х 0 = 4, у 0 = 2.
Таким образом,  з) Центр описанной окружности находится в точке пересечения серединных перпендикуляров.
з) Центр описанной окружности находится в точке пересечения серединных перпендикуляров.
 Координаты середин сторон АС и АВ найдены в п.в): С 2 (4, -1/2), В 2 (2, 7/2 ).
Уравнения линий серединных перпендикуляров
Координаты середин сторон АС и АВ найдены в п.в): С 2 (4, -1/2), В 2 (2, 7/2 ).
Уравнения линий серединных перпендикуляров 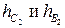 находим аналогично вычислениям в п.б).
Угловые коэффициенты находим аналогично вычислениям в п.б).
Угловые коэффициенты 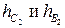 равны 2 и -2 соответственно, и эти прямые проходят через точки С 2 и В 2, их уравнения имеют вид: равны 2 и -2 соответственно, и эти прямые проходят через точки С 2 и В 2, их уравнения имеют вид:
 Система уравнений, составленная из уравнений серединных перпендикуляров:
Система уравнений, составленная из уравнений серединных перпендикуляров:
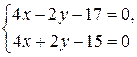 ,
имеет решение х = 4, у = -1/2.
Следовательно, центр описанной окружности находится в точке О 2 (4, -1/2).
Центр описанной окружности прямоугольного треугольника лежит на середине АВ: ,
имеет решение х = 4, у = -1/2.
Следовательно, центр описанной окружности находится в точке О 2 (4, -1/2).
Центр описанной окружности прямоугольного треугольника лежит на середине АВ: 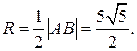 и) Центр тяжести треугольника находится в точке пересечения медиан.
1) Из п.в) имеем систему уравнений для определения координат центра тяжести как точки пересечения медиан mС и mB:
и) Центр тяжести треугольника находится в точке пересечения медиан.
1) Из п.в) имеем систему уравнений для определения координат центра тяжести как точки пересечения медиан mС и mB: 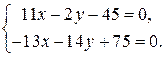 Система имеет решение х =4,33, у = 1,3. Следовательно, центр тяжести треугольника находится в точке О 3 (4,33; 1,3).
2) Укажем, что медианы треугольника делятся точкой пересечения в отношении 2: 1, считая от вершины.
Таким образом, координаты центра тяжести могут быть найдены как координаты точки О3, делящей медиану в отношении
Система имеет решение х =4,33, у = 1,3. Следовательно, центр тяжести треугольника находится в точке О 3 (4,33; 1,3).
2) Укажем, что медианы треугольника делятся точкой пересечения в отношении 2: 1, считая от вершины.
Таким образом, координаты центра тяжести могут быть найдены как координаты точки О3, делящей медиану в отношении  Если воспользоваться формулами деления отрезка в данном отношении, то координаты точки:
Если воспользоваться формулами деления отрезка в данном отношении, то координаты точки:
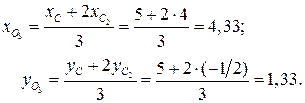 и) Внутренние углы треугольника могут быть найдены через угловые коэффициенты прилежащих сторон. Например, внутренний угол при вершине А треугольника
и) Внутренние углы треугольника могут быть найдены через угловые коэффициенты прилежащих сторон. Например, внутренний угол при вершине А треугольника 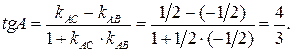 Следовательно, Ð А = arctg(4/3).
к) По формуле площади треугольника имеем
1)
Следовательно, Ð А = arctg(4/3).
к) По формуле площади треугольника имеем
1) 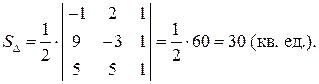 2) Площадь треугольника может быть вычислена по формуле:
SD = p × r,
где p – полупериметр треугольника; r – радиус вписанной окружности.
Поскольку
2) Площадь треугольника может быть вычислена по формуле:
SD = p × r,
где p – полупериметр треугольника; r – радиус вписанной окружности.
Поскольку 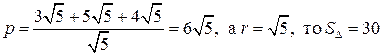 (кв. ед.).
(кв. ед.).
| а)
А (-1, 2),
В (9, -3),
С (5, 5),
б)
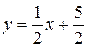 ,
у=- 2 х+ 15,
у= 2 х– 5,
в)
x+ 8 y– 15 = 0,
13 х+ 14 у– 75 = 0,
11 х– 2 у– 45 = 0,
г) ,
у=- 2 х+ 15,
у= 2 х– 5,
в)
x+ 8 y– 15 = 0,
13 х+ 14 у– 75 = 0,
11 х– 2 у– 45 = 0,
г) 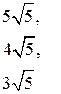 ,
д)
у = 2,
х+у– 6=0,
3 х–у– 10=0,
ж)
О 1(4,2), ,
д)
у = 2,
х+у– 6=0,
3 х–у– 10=0,
ж)
О 1(4,2),  ,
з)
О 2(4,-1/2), ,
з)
О 2(4,-1/2),  ,
и) ,
и) 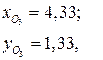 ,
к) 30. ,
к) 30.
|
| ПП 7.1. №2. | Найдите проекцию точки Р (4, 9) на прямую, проходящую через точки А (3, 1) и В (5, 2).
Решение:
Искомую точку М 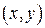 найдем, решая совместно уравнение прямой АВ с уравнением перпендикуляра, проведенного к этой прямой из точки Р. найдем, решая совместно уравнение прямой АВ с уравнением перпендикуляра, проведенного к этой прямой из точки Р.
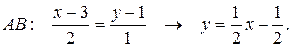 Уравнение перпендикуляра из точки Р на прямую АВ ищем в виде у – 9 = k (x – 4); из условия перпендикулярности
Уравнение перпендикуляра из точки Р на прямую АВ ищем в виде у – 9 = k (x – 4); из условия перпендикулярности 
 М М 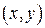 = = 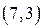
| 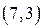
|
| ПП 7.1. №3. | Постройте прямую 3 х – 5 у + 15 = 0.
Решение:
 Уравнение прямой в отрезках имеет вид:
Уравнение прямой в отрезках имеет вид:  прямая отсекает на осях отрезки (-5) и 3. прямая отсекает на осях отрезки (-5) и 3.
| 5 х + 12 у+ + 6 = 0 |
| ПП 7.1. №4. | Даны две прямые 2 х + 3 у – 5 = 0, 7 х + 15 у + 1 = 0, пересекающиеся в точке М. Составьте уравнение прямой, которая проходит через точку М перпендикулярно к прямой 12 х – 5 у – 1 = 0.
Решение:
Прямые 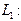 2 х + 3 у – 5 = 0, 2 х + 3 у – 5 = 0,  , ,
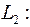 7 х + 15 у + 1 = 0, 7 х + 15 у + 1 = 0,  пересекаются, так как они имеют разные угловые коэффициенты. Составим уравнение пучка прямых, проходящих через точку их пересечения М:
2 х + 3 у – 5 + l×(7 х + 15 у + 1) = 0,
(2 + 7l)× х + (3 + 15l)× у + (-5 + l) = 0
Выделим в этом пучке искомую прямую пересекаются, так как они имеют разные угловые коэффициенты. Составим уравнение пучка прямых, проходящих через точку их пересечения М:
2 х + 3 у – 5 + l×(7 х + 15 у + 1) = 0,
(2 + 7l)× х + (3 + 15l)× у + (-5 + l) = 0
Выделим в этом пучке искомую прямую  . По условию искомая прямая перпендикулярна прямой . По условию искомая прямая перпендикулярна прямой  12 х – 5 у – 1 = 0, для которой 12 х – 5 у – 1 = 0, для которой  . .
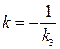 , ,  l = -1 и уравнение искомой прямой принимает вид:
5 х + 12 у + 6 = 0. l = -1 и уравнение искомой прямой принимает вид:
5 х + 12 у + 6 = 0.
| |
| ПП 7.1. №5. | Напишите уравнение прямой L, проходящей через точку М (2, 1) под углом 45° к прямой L1: 2 х + 3 у + 4 = 0.
Решение: 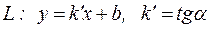 L1: 2 х + 3 у + 4 = 0,
L1: 2 х + 3 у + 4 = 0, 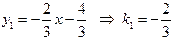 . .
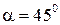 , , 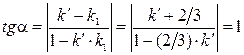  М (2,1) М (2,1) 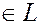 , , 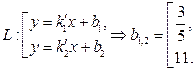

|
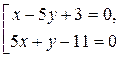
|
| ПП 7.1. №6. | Составьте уравнение прямой L, параллельной прямым L1: х + 2 у – 1 = 0
и L2: х + 2 у + 2 = 0 и проходящей посередине между ними.
 Решение:
1-ый способ. Уравнение прямой L будем искать в виде А (х – х 0) + В (у + у 0) = 0. В качестве нормального вектора
Решение:
1-ый способ. Уравнение прямой L будем искать в виде А (х – х 0) + В (у + у 0) = 0. В качестве нормального вектора  можно выбрать нормальный вектор прямых L1 и L2, равный
{1, 2}. Найдем какую-нибудь точку М 0 (х0, у 0) Î L. Точка М 0 будет делить пополам отрезок, соединяющий две любые точки, лежащие на L 1 и L 2. Например, М 1 (1, 0 ) Î L 1 и М 2 (-2, 0 ) Î L2, тогда точка М 0 имеет координаты (-1/2, 0), и уравнение прямой L принимает вид:
х + 2 у + 1/2 = 0.
2 –ой способ. Произвольная точка М (х, у) Î L, если
| d (М, L 1) | = | d (М, L 2) |.
Для снятия модуля определим знаки отклонений точки М (х, у) от прямых L1 и L2. Для этого нужно выяснить взаимное расположение начала координат, точки М (х, у) и прямых L 1 и L2.
Приведем уравнения прямых к нормальному виду: можно выбрать нормальный вектор прямых L1 и L2, равный
{1, 2}. Найдем какую-нибудь точку М 0 (х0, у 0) Î L. Точка М 0 будет делить пополам отрезок, соединяющий две любые точки, лежащие на L 1 и L 2. Например, М 1 (1, 0 ) Î L 1 и М 2 (-2, 0 ) Î L2, тогда точка М 0 имеет координаты (-1/2, 0), и уравнение прямой L принимает вид:
х + 2 у + 1/2 = 0.
2 –ой способ. Произвольная точка М (х, у) Î L, если
| d (М, L 1) | = | d (М, L 2) |.
Для снятия модуля определим знаки отклонений точки М (х, у) от прямых L1 и L2. Для этого нужно выяснить взаимное расположение начала координат, точки М (х, у) и прямых L 1 и L2.
Приведем уравнения прямых к нормальному виду:
 где
где 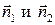 - единичные векторы нормалей к прямым L1 и L2, проведенным из начала координат.
Видим, что - единичные векторы нормалей к прямым L1 и L2, проведенным из начала координат.
Видим, что 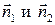 противоположны по направлению, значит, начало координат лежит в полосе между прямыми L1 и L2. Точка М и начало координат лежат по одну сторону как от прямой L1, так и от прямой L 2, значит, отклонения точки М от прямых L 1 и L 2 имеют один и тот же отрицательный знак.
Из противоположны по направлению, значит, начало координат лежит в полосе между прямыми L1 и L2. Точка М и начало координат лежат по одну сторону как от прямой L1, так и от прямой L 2, значит, отклонения точки М от прямых L 1 и L 2 имеют один и тот же отрицательный знак.
Из  следует, что
х + 2 у – 1 = -х – 2 у – 2 и х + 2 у + 1/2 = 0. следует, что
х + 2 у – 1 = -х – 2 у – 2 и х + 2 у + 1/2 = 0.
| х+ 2 у+ 1/2=0 |






