Прямая на плоскости.
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

| -расстояние между точками A (x 1 ,y 1) и B (x 2 ,y 2); |

|
-координаты точки С (x,y), которая делит отрезок, соединяющий точки A (x 1 ,y 1) и B (x 2 ,y 2), в отношении  ; ;
|

| -координаты середины отрезка АВ; |
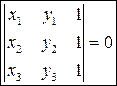
| -условие принадлежности трёх точек (x 1 ,y 1), (x 2 ,y 2), (x3,y 3) одной прямой; |

| - площадь треугольника с вершинами (x 1 ,y 1), (x2,y 2), (x 3 ,y 3). |
Прямая на плоскости
| Ax+By+C =0 | - общее уравнение прямой; |
| A(x-x 0 )+B(y-y 0 )= 0 | - уравнение прямой, проходящей через точку (x 0 ,y 0) перпендикулярно нормальному вектору { A,B }; |

| - каноническое уравнение прямой, проходящей через точку (x 0 ,y 0) параллельно вектору { l,m }; |

|
- параметрические уравнения прямой, проходящей через точку (x 0 ,y 0) параллельно вектору  ; ;
|

| - уравнение прямой, проходящей через две заданные точки (x 1 ,y 1) и (x 2 ,y 2); |

|
- уравнение прямой с угловым коэффициентом k, где  - угол наклона прямой к оси ox; - угол наклона прямой к оси ox;
|

| - уравнение прямой в отрезках, где (а, 0) и (0,b) - координаты точек пересечения прямой с осями ox и oy; |

| - нормальное уравнение прямой, где р - расстояние от начала координат до прямой, a-угол между осью ox и перпендикуляром к прямой, проходящим через начало координат; |

| - нормальный вид общего уравнения прямой; знак нормирующего множителя противоположен знаку С; |

| - расстояние от точки (x 0 ,y 0) до прямой Ax+By+C=0; |

| - координаты точек пересечения двух прямых A 1 x+B 1 y+C 1=0 и A 2 x+B 2 y+C 2=0; |

| - координаты точек пересечения прямых y=k 1 x+b 1 и y=k 2 x+b 2; |

| - условия параллельности прямых, заданных в общем виде A 1 x+B 1 y+ C1 =0, A 2 x+B 2 y+C 2 =0 и в виде y=k1x+b1, y=k2x+b2; |

| - условие перпендикулярности прямых, заданных в общем виде A 1 x + B 1 y + C 1=0, A 2 x + B 2 y + C 2=0 и в виде y=k 1 x+b 1, y=k2x+b 2; |

|
- угол  между двумя прямыми, заданными в общем виде A 1 x+B 1 y+C 1 =0, A 2 x+B 2 y+C 2 =0
и в виде y=k 1 x+b 1, y=k 2 x+b 2; между двумя прямыми, заданными в общем виде A 1 x+B 1 y+C 1 =0, A 2 x+B 2 y+C 2 =0
и в виде y=k 1 x+b 1, y=k 2 x+b 2;
|
A 1 x+B 1 y+C 1+
+ 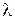 (A 2 x+B 2 y+C 2)=0 (A 2 x+B 2 y+C 2)=0
| - уравнение пучка прямых через точку М, если A 1 x+B 1 y+C 1=0 и A 2 x+B 2 y+C 2=0 - уравнения двух прямых, пересекающихся в точке М. |
Простейшие задачи на плоскости
Расстояние между двумя точками
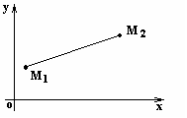 M 1(x 1, y 1), M 2(x 2, y 2)
M 1(x 1, y 1), M 2(x 2, y 2)
.
Деление отрезка в данном отношении
 Точка M (x,y) делит отрезок M 1 M 2 в отношении
Точка M (x,y) делит отрезок M 1 M 2 в отношении  , если
, если  . Тогда
. Тогда  а отсюда
а отсюда  и координаты точки М находятся по формулам:
и координаты точки М находятся по формулам:  .
.
Координаты середины отрезка С получаются при М 1 М = ММ 2, то есть  :
:

Отметим, что число l не зависит от того, как выбрано положительное направление на отрезке М 1 М 2, так как при изменении направления на противоположное l не меняется.
Прямая линия на плоскости
Общее уравнение прямой
Общее уравнение прямой на плоскости xoy получается из общего уравнения плоскости в пространстве при z = 0.
Прямая на плоскости в декартовых координатах задается уравнением
Ax+By+C =0.
Если А = 0 (В = 0), то прямая параллельна оси ox (оси oy). Если С =0, то прямая проходит через начало координат. Если прямая проходит через точку (x 0, y 0) перпендикулярно вектору  , ее уравнение принимает вид:
, ее уравнение принимает вид:  .
.
Канонические и параметрические уравнения прямой
Если прямая проходит через точку (x 0, y 0) параллельно направляющему вектору  , то из канонических и параметрических уравнений прямой в пространстве при z = 0 получаем каноническое и параметрические уравнения прямой на плоскости в виде
, то из канонических и параметрических уравнений прямой в пространстве при z = 0 получаем каноническое и параметрические уравнения прямой на плоскости в виде
 и
и 
где t – параметр,  .
.






