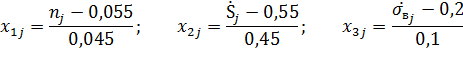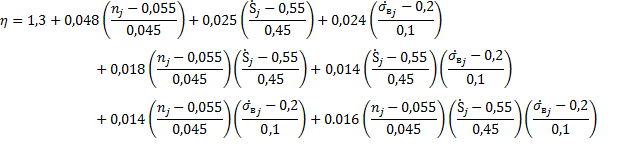Министерство образования и науки Российской Федерации
Санкт – Петербургский политехнический университет Петра Великого
Институт металлургии, машиностроения и транспорта
Кафедра ‹‹Технология конструкционных материалов и материаловедение››
Потапов Н.М.
ДИСЦИПЛИНА: « Основы научных исследований, организация и планирование эксперимента »
Пояснительная записка
К курсовой работе
Основы теории подобия и размерностей, построение линейных, квазилинейных и нелинейных уравнений регрессии
Направление подготовки бакалавров: 150700.62 “Машиностроение” _______ _________________________________________________________________
(код и наименование)
Профиль ООП: Машины и технологии обработки металлов давлением __________________________________________________________________
(код СПбПУ и наименование)
Группа 53304/11
Руководитель проекта: Востров В.Н.
профессор.д.т.н.
Допущен к защите:Заведующий кафедрой
‹‹___››_________2016 г. Радкевич М.М.
_____________________________
(подпись) (фамилия,инициалы)
САНКТ – ПЕТЕРБУРГ
2016
1. Оглавление
Задание №1. Основы теории подобия и размерностей. 3
Задание №2. Планирование эксперимента. Построение линейных и квазилинейных уравнений регрессии 6
Построение квазилинейной регрессионной модели. 9
Выполнение критериальных проверок. 11
Задание №3 Планирование эксперимента. Построение нелинейных уравнений регрессии/. 12
Выполнение критериальных проверок. 18
Проверка адекватности регрессионной модели. 19
Анализ остатков. 21
Погрешности моделей. 23
Задание №1. Основы теории подобия и размерностей
Вариант 15
Высадку сплошных валов с буртом на образующей части осуществляют на однопозиционных автоматах. Однопозиционные автоматы совмещают отрезку мерной заготовки от прутка и одну штамповую позицию. Принципиальная схема высадки приведена на рисунке 1. Заготовка 1 устанавливается в матрицу 2, которая закреплена в обойме 3. Подводится блок 5 с закрепленным в нем высадочным пуансоном 4, который и осуществляет процесс высадки буртовой части металла. Для извлечения готовой детали из пуансона и матрицы предусмотрены выталкиватели 6 и 7. Установить в критериальной форме функциональную связь усилия деформирования P с факторами.
Рисунок 1 – Схема высадки на однопозиционном автомате.
Решение
Функциональная зависимость, подлежащая исследованию:
Выберем три величины: 
. Докажем, что применительно к системе измерений основных величин MLT эти величины являются независимыми. Уравнения размерностей для данных величин:
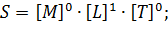
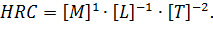
Вычислим определитель, составленный из показателей степеней в уравнениях размерностей:
Следовательно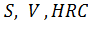 
– независимые величины..
Запишем уравнения размерностей для остальных параметров:
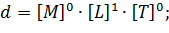
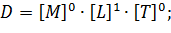
Представим безразмерные 
в виде отношений произвольной величины к независимым величинам:
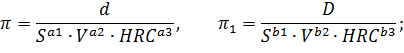
Подставим в формулы 
размерности величин параметров.
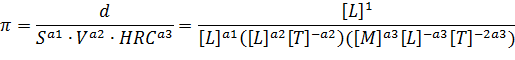
Сравниваем показатели одноименных основных величин:
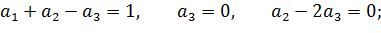
Отсюда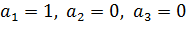 
. Безразмерный комплекс 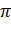имеет вид:
Аналогично выразим остальные -комплексы:
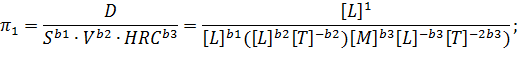
Сравниваем показатели одноименных основных величин:
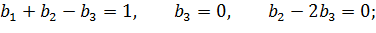
Отсюда 
. Безразмерный комплекс 
имеет вид:
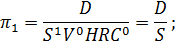
Задание №2. Планирование эксперимента. Построение линейных и квазилинейных уравнений регрессии
Вариант 5
Глубина шлифования H зависит от количества оборотов шлифовального круга n, подачи S и предела прочности 
материала заготовки, представленных в таблице:
Таблица 1 – Зависимость глубины шлифования
| Номер | n, об/мин |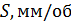 
| 
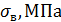
| H, мм | ||
| 0,1 | 1,0 | 0,3 | 1,41 | 1,52 | ||
| 0,1 | 0,1 | 0,3 | 1,39 | 1,24 | ||
| 0,1 | 1,0 | 0,1 | 1,29 | 1,36 | ||
| 0,1 | 0,1 | 0,1 | 1,29 | 1,31 | ||
| 0,1 | 0,2 | 0,3 | 1,42 | 1,35 | ||
| 0,055 | 1,0 | 0,3 | 1,35 | 1,28 | ||
| 0,055 | 0,2 | 0,2 | 1,32 | 1,32 | ||
| 0,01 | 1,0 | 0,1 | 1,26 | 1,25 | ||
| 0,01 | 1,0 | 0,3 | 1,25 | 1,29 | ||
| 0,01 | 0,1 | 0,2 | 1,20 | 1,18 | ||
| 0,01 | 0,1 | 0,3 | 1,27 | 1,25 | ||
| 0,01 | 0,1 | 0,1 | 1,29 | 1,18 |
1. Выбрать из таблицы данные для составления плана эксперимента;
2. Построить квазилинейную регрессионную модель;
3. Выполнить критериальные проверки.
Решение
Составление плана эксперимента
В нашем опыте независимыми переменными являются скорость вращения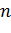 
, величина подачи S и прочность материала 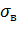, зависимой переменной является глубина шлифования H.
Для математической обработки данных эксперимента необходимо перейти от реальных физических величин к нормированным, т.е. расположенным в интервале 
.
Интервалы изменения площади вырезаемого грунта, ширины ковша и прочности грунта:
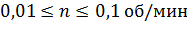
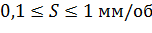
МПа
Вычислим основной уровень для изменения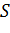 
, h и k:
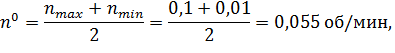
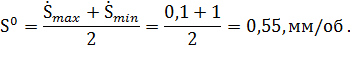
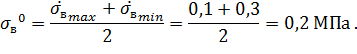
Вычислим интервал варьирования для изменения n,S,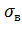 
:
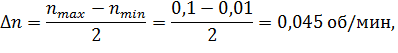
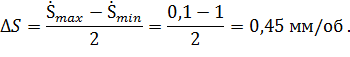
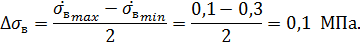
Нормированные значения факторов обозначим через 
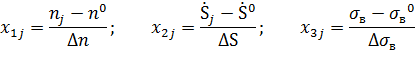
В результате получим план эксперимента:
Таблица 2 – План эксперимента
| № опыта | Факторы | Значения отклика в повторных опытах | Выборочное среднее отклика | |||
| i |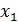 
| 
| 
| 
| 
| 
|
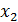
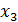
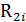
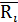
| 1,41 | 1,52 | 1,5 | ||||
| -1 | 1,39 | 1,24 | 1,3 | |||
| -1 | 1,29 | 1,36 | 1,3 | |||
| -1 | -1 | 1,29 | 1,31 | 1,3 | ||
| 1,42 | 1,35 | 1,4 | ||||
| 1,35 | 1,28 | 1,3 | ||||
| 1,32 | 1,32 | 1,3 | ||||
| -1 | -1 | 1,26 | 1,25 | 1,3 | ||
| -1 | 1,25 | 1,29 | 1,3 | |||
| -1 | -1 | 1,2 | 1,18 | 1,2 | ||
| -1 | -1 | 1,27 | 1,25 | 1,3 | ||
| -1 | -1 | -1 | 1,29 | 1,18 | 1,2 |
Количество опытов в плане полного факторного эксперимента определяется по формуле:
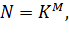(1.1)
Где K – количество уровней, M – количество факторов.
План эксперимента из таблицы 2 не соответствует соотношению (1.1), так как 12≠63, следовательно необходимо исключить из плана два уровня факторов, чтобы соотношение (1.1.) приняло вид 8=23.
Оставим в плане только максимальные и минимальные уровни факторов, с целью увеличить интервал варьирования и избежать в дальнейшем получения незначимых коэффициентов квазилинейной модели.
Тогда план полного факторного эксперимента примет следующий вид:
Таблица 3 – План полного факторного эксперимента
| № опыта | Факторы | Значения отклика в повторных опытах | Выборочное среднее отклика | |||
| i |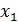
|
|
|
|
|
|
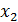
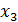
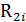
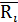
| 1,41 | 1,52 | 1,465 | ||||
| -1 | 1,39 | 1,24 | 1,315 | |||
| -1 | 1,29 | 1,36 | 1,325 | |||
| -1 | -1 | 1,29 | 1,31 | 1,3 | ||
| -1 | -1 | 1,26 | 1,25 | 1,255 | ||
| -1 | 1,25 | 1,29 | 1,27 | |||
| -1 | -1 | 1,27 | 1,25 | 1,26 | ||
| -1 | -1 | -1 | 1,29 | 1,18 | 1,235 |
Данный план является полным, т.к. обладает следующими свойствами:
· Алгебраическая сумма элементов вектора-столбца каждого фактора равна нулю. Данное свойство называется симметричностью плана:
· Сумма почленных произведений любых двух векторов-столбцов равна нулю: 
· Сумма квадратов элементов столбца каждого фактора равна количеству опытов N:
Построение квазилинейной регрессионной модели
Построим квазилинейную статистическую (регрессионную) модель вида:
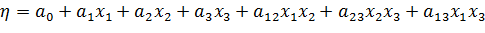
Для нахождения коэффициентов am модели воспользуемся свойствами вектор-столбцов полного факторного эксперимента. Это позволит вычислить их по формулам:
; 
; 
; 
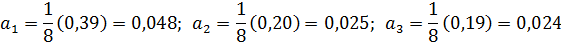
Получили модель:
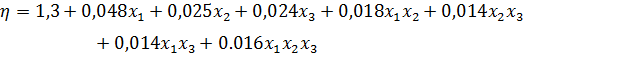
Перейдём от нормированных значений факторов к их натуральным значениям:
