ЗАДАНИЕ N 36 сообщить об ошибке
ЗАДАНИЕ N 36 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения  удовлетворяющее условию
удовлетворяющее условию  имеет вид …
имеет вид …

| 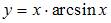
| ||

| |||

| |||

|
Решение:
Уравнение 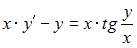 перепишем в виде
перепишем в виде  Сделаем замену
Сделаем замену  Тогда
Тогда 
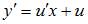 и уравнение запишется в виде
и уравнение запишется в виде  Разделим переменные
Разделим переменные  и проинтегрируем обе части последнего уравнения:
и проинтегрируем обе части последнего уравнения:  Тогда
Тогда  Сделаем обратную замену:
Сделаем обратную замену:  Подставим в найденное общее решение начальное условие
Подставим в найденное общее решение начальное условие  Тогда
Тогда  и
и  Следовательно, частное решение имеет вид
Следовательно, частное решение имеет вид 
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения  удовлетворяющее условию
удовлетворяющее условию  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Сделаем замену  Тогда
Тогда 
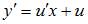 и уравнение запишется в виде
и уравнение запишется в виде 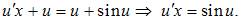 Разделим переменные
Разделим переменные  и проинтегрируем обе части последнего уравнения:
и проинтегрируем обе части последнего уравнения:  Тогда
Тогда  и
и  Сделаем обратную замену:
Сделаем обратную замену: 
Подставим в найденное общее решение начальное условие 
Тогда 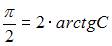 и
и  Следовательно, частное решение имеет вид
Следовательно, частное решение имеет вид 
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Частный интеграл дифференциального уравнения  удовлетворяющий начальному условию
удовлетворяющий начальному условию 
имеет вид …

| 
| ||
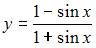
| |||

| |||
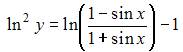
|
 ЗАДАНИЕ N 33 сообщить об ошибке
ЗАДАНИЕ N 33 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Решение задачи Коши  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Уравнение  перепишем в виде
перепишем в виде  Введем замену
Введем замену 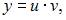
 Получим:
Получим:  или
или 
Пусть  Тогда
Тогда  Подставим найденное значение u
Подставим найденное значение u
в уравнение  Получим:
Получим:  То есть
То есть  и
и  Тогда общее решение примет вид
Тогда общее решение примет вид 
Подставим в найденное общее решение начальное условие 
тогда 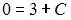 и
и 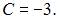 Следовательно, частное решение имеет вид
Следовательно, частное решение имеет вид 
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения 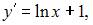 удовлетворяющее условию
удовлетворяющее условию  имеет вид …
имеет вид …

| 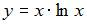
| ||

| |||

| |||

|
Решение:
Проинтегрируем обе части уравнения:  Подставив условие
Подставив условие  получим
получим  и
и 
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения  удовлетворяющее условию
удовлетворяющее условию  имеет вид …
имеет вид …

| 
| ||

| |||

| |||
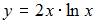
|
 ЗАДАНИЕ N 32 сообщить об ошибке
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения  удовлетворяющее условию
удовлетворяющее условию  имеет вид …
имеет вид …

| 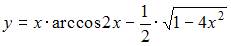
| ||

| |||

| |||

|
Решение:
Проинтегрируем обе части уравнения: 
Подставив условие  получим С = 0 и
получим С = 0 и 
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Решение задачи Коши  имеет вид …
имеет вид …

| 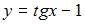
| ||

| |||
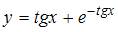
| |||

|
Решение:
Уравнение 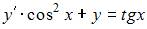 перепишем в виде
перепишем в виде  Введем замену
Введем замену 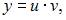
 Получим:
Получим:  или
или 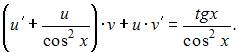
Пусть  Тогда
Тогда 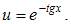 Подставим найденное значение u
Подставим найденное значение u
в уравнение 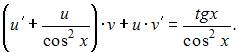
Получим:  То есть
То есть  и
и 
Тогда общее решение примет вид 
Подставим в найденное общее решение начальное условие  тогда
тогда  и
и  Следовательно, частное решение имеет вид
Следовательно, частное решение имеет вид 
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Задача Коши для дифференциального уравнения первого порядка
Уравнение кривой, проходящей через точку  поднормаль которой в любой ее точке равна 4 имеет вид …
поднормаль которой в любой ее точке равна 4 имеет вид …

| 
| ||

| |||

| |||

|
Решение:
Поднормаль в произвольной точке равна 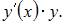 Тогда для нахождения уравнения искомой кривой получим уравнение
Тогда для нахождения уравнения искомой кривой получим уравнение 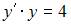 или
или  Проинтегрировав обе части этого уравнения, получим:
Проинтегрировав обе части этого уравнения, получим: 
Для вычисления значения C подставим в найденное решение координаты точки  Тогда
Тогда 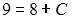 и
и  Следовательно, уравнение кривой имеет вид
Следовательно, уравнение кривой имеет вид