 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| уравнением с разделяющимися переменными | ||
| однородным относительно x и y дифференциальным уравнением первого порядка | |||
| линейным дифференциальным уравнением 1-го порядка | |||
| уравнением Бернулли |
Решение:
Данное уравнение можно представить в виде 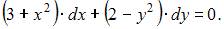 Откуда
Откуда 
Следовательно, это уравнение является уравнением с разделяющимися переменными.
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение 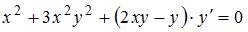 является …
является …

| уравнением с разделяющимися переменными | ||
| линейным дифференциальным уравнением 1-го порядка | |||
| однородным относительно x и y дифференциальным уравнением первого порядка | |||
| уравнением Бернулли |
Решение:
Данное уравнение можно представить в виде 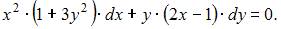
Откуда 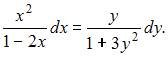
Следовательно, это уравнение является уравнением с разделяющимися переменными.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| однородным относительно x и y дифференциальным уравнением первого порядка | ||
| линейным неоднородным дифференциальным уравнением первого порядка | |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
Перепишем уравнение  в виде
в виде 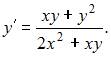
В уравнении  функция
функция 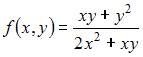 является однородной относительно
является однородной относительно 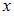 и
и 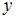 функцией нулевого порядка.
функцией нулевого порядка.
Действительно, 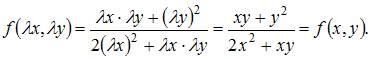
Поэтому данное уравнение является однородным относительно x и y дифференциальным уравнением первого порядка.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение 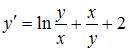 является …
является …

| однородным относительно x и y дифференциальным уравнением первого порядка | ||
| линейным неоднородным дифференциальным уравнением первого порядка | |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
В уравнении  функция
функция  является однородной относительно
является однородной относительно 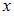 и
и 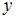 функцией нулевого порядка.
функцией нулевого порядка.
Действительно, 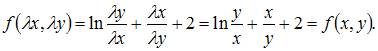
Поэтому данное уравнение является однородным относительно x и y дифференциальным уравнением первого порядка.
 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение 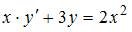 является …
является …

| линейным неоднородным дифференциальным уравнением первого порядка | ||
| однородным относительно x и y дифференциальным уравнением первого порядка | |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
Уравнение 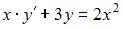 может быть сведено к уравнению вида
может быть сведено к уравнению вида 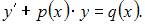 Действительно,
Действительно, 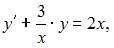 поэтому данное уравнение является дифференциальным линейным уравнением первого порядка.
поэтому данное уравнение является дифференциальным линейным уравнением первого порядка.
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение 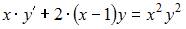 является …
является …

| уравнением Бернулли | ||
| линейным дифференциальным уравнением первого порядка | |||
| дифференциальным уравнением с разделяющимися переменными | |||
| однородным относительно x и y дифференциальным уравнением первого порядка |
Решение:
Уравнение 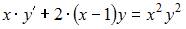 можно представить в виде
можно представить в виде 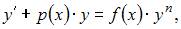 где
где 
Действительно, 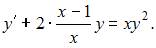 Поэтому данное уравнение является уравнением Бернулли.
Поэтому данное уравнение является уравнением Бернулли.
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение 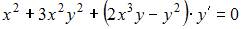 является …
является …

| уравнением в полных дифференциалах | ||
| уравнением с разделяющимися переменными | |||
| линейным дифференциальным уравнением 1-го порядка | |||
| однородным относительно x и y дифференциальным уравнением первого порядка |
Решение:
Данное уравнение можно представить в виде 
Обозначим 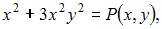
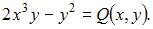
Тогда 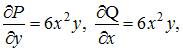 то есть
то есть 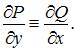
Следовательно, это уравнение является уравнением в полных дифференциалах.
 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| дифференциальным уравнением первого порядка в полных дифференциалах | ||
| однородным относительно x и y дифференциальным уравнением первого порядка | |||
| линейным неоднородным дифференциальным уравнением первого порядка | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
Если в дифференциальном уравнении вида 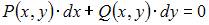 выполняется условие
выполняется условие 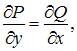 то оно является дифференциальным уравнением первого порядка в полных дифференциалах.
то оно является дифференциальным уравнением первого порядка в полных дифференциалах.
В нашем случае  и
и 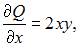 поэтому данное уравнение является дифференциальным уравнением первого порядка в полных дифференциалах.
поэтому данное уравнение является дифференциальным уравнением первого порядка в полных дифференциалах.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение  является …
является …

| дифференциальным уравнением первого порядка в полных дифференциалах | ||
| однородным относительно x и y дифференциальным уравнением первого порядка | |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
Решение:
Если в дифференциальном уравнении вида 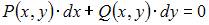 выполняется условие
выполняется условие 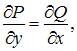 то оно является дифференциальным уравнением первого порядка в полных дифференциалах.
то оно является дифференциальным уравнением первого порядка в полных дифференциалах.
В нашем случае 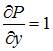 и
и  поэтому данное уравнение является дифференциальным уравнением первого порядка в полных дифференциалах.
поэтому данное уравнение является дифференциальным уравнением первого порядка в полных дифференциалах.
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Типы дифференциальных уравнений
Уравнение 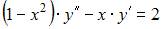 является …
является …

| дифференциальным уравнением второго порядка, допускающим понижение порядка | ||
| линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами | |||
| линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами | |||
| уравнением Эйлера |






