1.2.4.1 (SISO - singl-input-singl-output) без сигнала обхода. Математическое описание системы в общем виде следующее
, 
, 
. (1.16)
В развернутом виде описание системы (1.16) следующее
(1.17)
В скалярном виде описание системы (1.16) следующее
(1.18)
Помимо устойчивостидля данной системы существуют такие понятия, как свойство полной управляемости и свойство полной наблюдаемости. Структура системы представлена на рисунке 6.
1.2.4.2 (SISO - singl-input-singl-output) с сигналом обхода. Математическое описание системы в общем виде следующее
, , 
. (1.19)
В развернутом виде описание системы (1.19) следующее
(1.20)
В скалярном виде описание системы (1.19) следующее
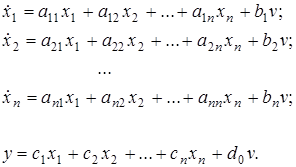(1.21)
Помимо устойчивостидля данной системы существуют такие понятия, как свойство полной управляемости и свойство полной наблюдаемости. Структура системы представлена на рисунке 7.
1.2.4.3 (SIМO - singl-input-multi-output). Математическое описание системы в общем виде следующее
, , 
. (1.22)
В развернутом виде описание системы (1.22) следующее
(1.23)
В скалярном виде описание системы (1.22) следующее
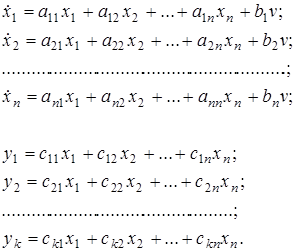(1.24)
Помимо устойчивостидля данной системы существуют такие понятия, как свойство полной управляемости и свойство полной наблюдаемости. Структура системы представлена на рисунке 8.
1.2.4.4 (MISO - multi-input-singl-output). Математическое описание системы в общем виде следующее
, , . (1.25)
В развернутом виде описание системы (1.25) следующее
(1.26)
В скалярном виде описание системы (1.25) следующее
(1.27)
Помимо устойчивостидля данной системы существуют такие понятия, как свойство полной управляемости и свойство полной наблюдаемости. Структура системы представлена на рисунке 9.
1.2.4.4 (MIМO - multi-input-multi-output) без матрицы обхода. Математическое описание системы в общем виде следующее
, , 
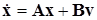. (1.28)
В развернутом виде описание системы (1.28) следующее
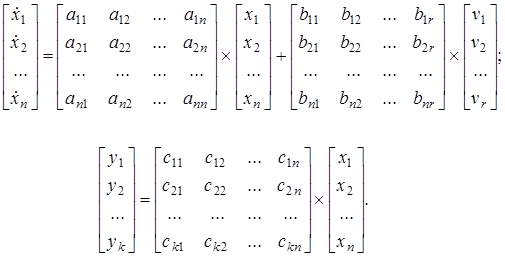(1.29)
В скалярном виде описание системы (1.28) следующее
(1.30)
Помимо устойчивостидля данной системы существуют такие понятия, как свойство полной управляемости и свойство полной наблюдаемости. Структура системы представлена на рисунке 10.
1.2.4.5 (MIМO - multi-input-multi-output) с матрицей обхода. Математическое описание системы в общем виде следующее
, , 
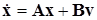. (1.31)
В развернутом виде описание системы (1.31) следующее
(1.32)
В скалярном виде описание системы (1.31) следующее
(1.33)
Помимо устойчивостидля данной системы существуют такие понятия, как свойство полной управляемости и свойство полной наблюдаемости. Структура системы представлена на рисунке 11.
1.3 Устойчивость систем. Для исследования рассмотренных систем на устойчивость необходимо определить матрицу
(1.34)
где 
- матрица состояния системы размера 
; 
- единичная матрица размера ; 
(
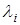) собственные числа матрицы состояния .
Для асимптотической устойчивости системы необходимо и достаточно, чтобы все корни (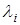
) характеристического уравнения
(1.34)
располагались в левой полуплоскости комплексной плоскости (имели отрицательные действительные части). Для проверки условий устойчивости можно воспользоваться любым известным критерием устойчивости для линейных систем.
1.3.1 Так для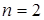 
характеристическое уравнение (1.34) будет иметь вид
(1.35)
Для устойчивости системы (при 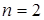) необходимо и достаточно, чтобы для уравнения (1.35) выполнялись условия: 
, 
, 
, или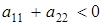 
, 
.
1.3.2 Для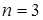 
характеристическое уравнение (1.34) будет иметь вид
(1.36)
где 
; 
;
;
.
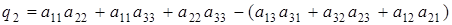Для устойчивости системы (при 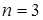) необходимо и достаточно, чтобы для уравнения (1.36) выполнялись условия: , 
(условия А.Стодолы) и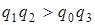 
(критерий И.А.Вышнеградского).
1.3.3 Для 
характеристическое уравнение (1.34) будет иметь вид
(1.37)
Для исследования устойчивости системы (при ) можно применить матрицу А.Гурвица
.
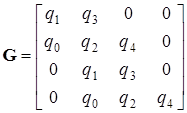Для устойчивости системы (при ) необходимо и достаточно, чтобы для уравнения (1.37) выполнялись условия: , , 
(условия А.Стодолы) и
, 
.
