Введем следующие понятия и обозначения.
n-множество – множество из n различных элементов:
Х = {х1, х2, …, хn}, хi ¹ хj, при i ¹ j.
(n) -множество – множество, содержащее n различных типов элементов:
Х = {х1, х1, …, х1, х2, х2, …, хn}.
r-выборка множества – совокупность из r элементов данного множества (если выборка из n-множества, то повторяющихся элементов нет, если из (n)-множества, то есть повторения).
Размещения – упорядоченные r-выборки (элементы прямого произведения Х1 ´ Х2 ´… ´ Хr).
Сочетания – неупорядоченные r-выборки (r-элементные подможества данного множества).
Задача 1.
а) На диске секретного замка 12 букв. Замок открывается после набора пароля из 5 букв.
В пароле буквы могут повторяться. Следовательно, каждый пароль – это 5-размещение из множества (12), т.е. размещение с повторениями.
б) Из 25 человек, членов комитета, надо выбрать: председателя, вице-председателя, секретаря и казначея (4 человека). Совмещение должностей не допускается.
В задаче повторение элементов невозможно, т.к. не допускается совмещение должностей. Кроме того, в данной 4-выборке важен порядок выбора, т.к. надо не просто выбрать заданное число человек, но необходимо связать каждого выбранного с определенной должностью. Следовательно, здесь речь идет о размещении без повторений.
в) Из 125 человек надо выбрать 6 делегатов на конференцию.
В данном случае порядок выбора не играет роли, следовательно, имеет место 6-сочетание из 125-множества.
Многие простые задачи комбинаторики решаются с помощью двух основных аксиоматических правил.
1. Правило суммы. Если все комбинации можно разбить на несколько непересекающихся классов, то общее число комбинаций равно сумме чисел комбинаций во всех классах:
.
2. Правило произведения. Пусть объект А можно выбрать n способами, а при каждом таком выборе объект В можно выбрать m способами. Тогда выбор упорядоченной пары (А, В) можно сделать n×m способами. В общем случае:
.
На практике оба правила часто используются в комбинации.
Задача 2. Сколькими способами можно из 28 костей домино выбрать 2 кости, которые можно приложить друг к другу?
Решение. 1-ю кость можно выбрать 28-ю способами. Из них в 7 случаях кость будет дублем, а в 21 случаях – с различными числами. Если 1-я кость является дублем, 2-ю кость можно выбрать 6-ю способами, а если – нет, то 12-ю способами. В соответствии с правилами суммы и произведения общее число случаев равно N = 7×6 + 21×12 = 294.
Пример 3. В азбуке Морзе самый длинный код буквы состоит из 5 символов. Можно ли использовать коды длиной не более 4-х символов?
Решение. В соответствии с правилом суммы число различных кодов длиной не более 4 символов при использовании 2 видов символов (точка и тире) равно 
= 2 + 4 + 8 + 16 = 30. Значит, 4-х символьных кодов не хватит для кодирования даже всех букв кириллицы, не говоря о служебных символах. При использовании же 5-ти символьных кодов N = 30 + 
= 62, т.е. такой длины кода достаточно.
Пример 1.4. Найти все перестановки букв в слове “мама”.
Решение. В данном слове есть объекты 2-х типов – “м” и “а”. Всего множество содержит 4 элемента. Следовательно, число перестановок равно 
. Действительно, имеем следующие комбинации: ”аамм”, “мама”, “амам”, “ммаа”, “амма”, “маам”.
Пример 1.5. Найти число перестановок букв в слове “Миссисипи”.
Решение. Длина этого слова – 9 букв. Из них буква “м” встречается 1 раз, “и” – 4 раза, “с” – 3, “п” – 1. Следовательно, число перестановок равно
Р(1, 4, 3, 1) = 
= 2520.
Пример 1.6. В лотерее из 36 номеров будут выбраны 5. Какова вероятность угадать ровно 3 номера из 5?
Решение. 3 номера из 5 верных можно выбрать 
способами. На каждый угаданный номер могут приходиться любые 2 из 31 невыбранных номеров, т.е. 
сочетаний. Окончательное число благоприятных случаев равно 
. Общее же число случаев равно количеству выпадения 5 номеров из 36, т.е. 
.
Отсюда вероятность угадывания равна 
» 0.0123 – немногим более 1%.
Пример 1.7. Определить количество N возможных сочетаний из 8 пирожных 4-х сортов.
Решение. В данном случае rj– число пирожных j-го сорта. Следовательно, r = 8, n = 4 и N =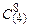 
= 
= 165.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Сколькими способами можно выбрать на шахматной доске белый и черный квадрат, не лежащие на одной и той же горизонтали и вертикали?
2. В корзине 12 яблок и 10 апельсинов. Ваня выбирает один фрукт, после чего Надя берёт оба фрукта. В каком случае у неё больше выбор?
3. Имеются 3 волчка с 6, 8 и 10 гранями. Сколькими различными способами могут они упасть? Та же задача, если известно, что, по крайней мере, 2 волчка упали на сторону помеченную цифрой 1.
4. В некотором государстве не было жителей с одинаковым набором зубов. Какова может быть максимальная численность населения такого государства?
5. Сколько различных пятизначных чисел можно составить, если каждая из цифр может повторяться несколько раз?
6. Сколько различных 4-х значных чисел, делящихся на 4 можно составить из цифр 1, 2, 3, 4, 5, если цифры могут повторяться?
7. В селении проживает 2000 жителей. Доказать, что по крайней мере двое из них имеют одинаковые инициалы.
8. Сколькими способами можно выбрать на шахматной доске белый и чёрный квадраты, не лежащие на одной и той же горизонтали и вертикали?
9. Сколькими способами можно поставить на доску 2 шашки (белую и черную), чтобы белая шашка не била черную?
10. Сколько слов, содержащих по 5 букв можно составить, если допускаются повторения, но никакие 2 соседние буквы не должны совпадать?
11. Автомобильные номера состоят из 1, 2 или 3 букв и 4 цифр. Найти число таких номеров, если используется 31 буква русского алфавита.
12. Флаг составляется из 7 горизонтальных полос 10 возможных цветов, причем любые 2 соседние полосы должны быть различных цветов. Сколькими способами это можно осуществить?
13. Имеются 3 курицы, 4 утки и 2 гуся. Сколько имеется ком-бинаций для выбора нескольких птиц, так чтобы среди выбран-ных были и куры, и утки и гуси.
14. Имеется 5 различных стульев и 7 рулонов различной обивочной ткани. Сколькими способами можно осуществить обивку стульев.
15. 15 занумерованных бильярдных шаров размещены по 6 лузам. Сколькими способами можно это сделать?
16. В классе 20 мальчиков и 20 девочек. Для концерта нужно выделить танцующий дуэт, дуэт певцов и гимнастов. Сколькими способами можно это сделать?
17. Компания из 7 юношей и 10 девушек танцует. Если в каком-то танце участвуют все юноши, то, сколько имеется вариантов участия девушек в этом танце? Сколько имеется вариантов, если учитывать лишь то, какие девушки остались неприглашёнными? Сколько имеется вариантов пар, если относительно 2-х девушек можно с уверенностью сказать, что они будут приглашены на танец? Сколько имеется в этом случае вариантов, если учитывать лишь то, какие девушки остались неприглашёнными?
18. 3 юношей и 2 девушки выбирают место для работы. В городе есть 3 завода, где требуются литейщики, 2 ткацкие фабрики, и 2 фабрики, где требуются и мужчины и женщины. Сколькими способами могут они распределиться между предприятиями?
19. Сколькими способами можно рассадить 12 человек за круглым столом?
20. На полке находится m + n различных книг, из которых m в чёрных переплётах, а n в красных. Сколько существует перестановок этих книг, при которых книги в чёрных переплётах занимают первые m мест? Сколько положений, в которых все книги в чёрных переплётах стоят рядом?
21. Из 20 сотрудников лаборатории 5 должны выехать в командировку, причём начальник и 2 ведущих инженера не могут выехать одновременно. Сколько можно составить различных составов групп?
22. Из цифр 1–5 составляют 5-значные числа, не кратные 5 и не содержащие одинаковых цифр. Сколько чисел можно составить?
23. Переплётчик должен переплести 12 различных книг в красный, зелёный и коричневый переплёты. Сколькими способами он может это сделать, если в каждый цвет должна быть переплетена хотя бы одна книга?
24. 30 человек разбиты на 3 группы, по 10 человек в каждой. Сколько может быть различных составов групп?
25. Сколько различных аккордов можно взять на 10 выбранных клавишах, если в аккорде от 3 до 7 звуков?
26. Сколькими способами n одинаковых подарков можно раздать 7 детям: а) без ограничений; б) если каждый ребёнок должен получить хотя бы один подарок?
27. 30 книг – 27 книг различных авторов и трехтомник – находятся на одной полке. Сколькими способами можно расставить эти книги, чтобы книги одного автора стояли рядом?
28. Имеется 20 наименований товаров. Сколькими способами можно распределить их по 3-м магазинам, если в первый магазин могло быть доставлено 8 наименований, во второй – 7, а в 3-й – 5?
29. Сколькими способами можно переставить буквы слова «ЛОГАРИФМ» так, чтобы 2-е, 4-е и 6-е места были заняты согласными буквами?
30. Сколько неотрицательных целых чисел меньше, чем 10 миллионов содержат цифры 2, 3, 4, 5, 6? Сколько чисел состоит только из этих цифр?
31. Сколькими способами можно переставить буквы слова «ПАСТУХИ» так, чтобы как гласные, так и согласные шли в алфавитном порядке?
32. Сколько нечётных чисел можно составить из цифр числа 53694 (каждую цифру можно использовать не более одного раза)? А чётных?
33. Сколько имеется шестизначных чисел, у которых 3 цифры – чётные, а 3 – нечётные? Сколько из этих чисел чётных?
34. Сколькими способами можно выбрать 4 буквы из слова «ТАРТАР», если не учитывать порядка выбранных букв?
35. Сколько четырёхзначных чисел можно составить из цифр числа 132132?
36. Имеются 10 яблок, 15 груш и 20 апельсинов. Сколькими способами можно разбить их на 3 группы по 10, 15 и 20 фруктов?
37. Множество A состоит из n различных элементов. Сколькими способами можно переставить элементы этого множества, чтобы два фиксированных элементов a и b не стояли рядом? Никакие два элемента, из элементов a, b, c не стояли рядом?
38. Сколькими способами можно составить набор из 8 пирожных, если имеется 4 сорта пирожных?
39. У мужа 15 знакомых – из них 5 женщин и 7 мужчин, а у жены – 7 женщин и 5 мужчин. Сколькими способами можно составить компанию из 6 мужчин и 6 женщин так, чтобы 6 человек пригласил муж и 6 – жена?
40. Сколько различных ожерелий можно составить из 7 одинаковых белых бусин, 10 красных и 15 чёрных?
41. Сколькими способами можно составить из 9 согласных слова, в которые входит 4 различных согласных и 3 различных гласных? В скольких из этих слов никакие две согласные не повторяются?
42. Поезду, в котором находится n пассажиров, предстоит сделать m остановок. Сколькими способами могут распределиться пассажиры между этими остановками? Та же задачи, если учитывается лишь количество пассажиров, вышедших на данной остановке.
43. В соревновании по гимнастике участвуют 10 человек. Трое судей должны независимо друг от друга перенумеровать их в порядке, отражающем их успехи в соревновании. Победителем считается тот, кого назовут первым хотя бы двое судей. В какой доле случаев победитель будет определён?
44. 30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует за одно предложение и учитывается лишь число голосов, поданных за каждое предложение?
45. Для премии на математической олимпиаде выделено 4 экземпляра одной книги, два экземпляра второй и два экземпляра третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовали 25 человек и никому не дают двух книг сразу? А если никому не дают двух экземпляров одной и той же книги, но могут быть вручены 2 или 3 различные книги?
