ОПРЕДЕЛЕНИЕ. Пусть А1, А2,..., Аn – некоторые множества. Их прямым или декартовым произведением называется множество упорядоченных наборов из n элементов, т.е.
А1´А2´... ´Аn = {(а1, а2,..., аn) | aiÎAi }.
Если все множества Ai совпадают A = А1 = А2 =... = Аn, то прямое произведение А1´А2´... ´Аn = An называют прямой n-ой степенью множества А.
Задача 1.. Доказать, что
(P´Q) \ (A´B) = ((P \ A)´Q) È (P´(Q \ B).
Решение.
1) Докажем включение (P´Q)\(A´B)Í((P\A)´Q)È (P´(Q\B)).
Пусть (x,y)Î(P´Q) \ (A´B), тогда (x,y)Î(P´Q) и (x,y)Ï(A´B). Это означает, что xÎP, yÎQ и либо xÏA, либо yÏB. В первом случае имеем xÎP, yÎQ, xÏA, следовательно, (x, y)Î(P \ A)´Q. Аналогично для второго случая получим, что (x, y)ÎP´(Q \ B). Следовательно, (x, y)Î((P \ A)´Q) È (P´(Q \ B)).
2) Докажем теперь обратное включение.
Так как (x, y)Î((P \ A)´Q) È (P´(Q \ B)), то (x, y)Î(P \ A)´Q или
(x, y)ÎP´(Q \ B). В первом случае получим, что xÎP, xÏA, yÎQ, во втором – xÎP, yÎQ, yÏB. Следовательно, в обоих случаях получим, (x, y)Î(P´Q) и (x, y)Ï(A´B), что и означает требуемое.
Бинарным отношением между элементами множеств А и В называется любое подмножество R Í A´B. Если множества A и B совпадают А = В, то R называют бинарным отношением на множестве А.
Если (x, y)ÎR, то это обозначают еще xRy и говорят, что между элементами x и y установлено бинарное отношение R.
Диагональ множества A´A, т.е. множество D={(x,x) | xÎA}, называется единичным бинарным отношением или отношением равенства в A.
Областью определения бинарного отношения R называется множество dR = { xÎA | $ yÎB, (x, y) ÎR }.
Областью значений бинарного отношения R называется множество rR = { yÎB | $ xÎA, (x, y)ÎR }.
Образом множества X относительно отношения R называется множество
R(X) = { yÎB | (x, y)ÎR, xÎX };
прообразом X относительно R называется R –1(X).
Операции над бинарными отношениями определяются подобно операциям над соответствующими множествами. Пусть А – произвольное множество на котором введены бинарные отношения R, R1, R2,...
3) Обратное отношение R –1 = { (x, y) | (y, x)ÎR}.
4) Дополнение к отношению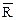 
={ (x, y) | (x, y)Î(A´A) \ R}.
5) Двойственное отношение Rd = 
.
6) Композиция (суперпозиция) отношений R = R1oR2 содержит пару (x, y) тогда и только тогда, когда существует такое zÎA, что (x, z)ÎR1 и (z, y)ÎR2.
Задача 2. Найти dR, rR, R –1, R o R, R o R –1, R –1 o R для отношения R = { (x, y) | x,yÎ N, x делит y }
Решение. dR={ xÎ N | yÎ N, x делит y }= N, так как для любого натурального x найдется yÎ N, например y = x, такой, что x делит y.
rR={ yÎ N | xÎ N, x делит y}= N, так как для любого натурального y найдется xÎ N, например x = 1, такой, что x делит y.
R –1 ={ (x, y) | x, yÎ N, y делит x }.
RoR={ (x, y)Î N 2 | $ zÎ N, x делит z и z делит y } = R, так как для любой пары (x, y)Î N 2, такой, что x делит y, такое значение z существует, например z = x.
RoR –1={ (x, y)Î N 2 | $ zÎ N, x делит z и y делит z }= N 2. Такое натуральное z существует для любой пары (x, y)Î N 2, например z=xy.
R –1oR={ (x, y)Î N 2 | $ zÎ N, z делит x и z делит y } = N 2. Такое натуральное z существует для любой пары (x, y)Î N 2, например z = 1.
Задача 3. Доказать тождество`R = (R–1 \ R) È (`R Ç Rd).
Решение.
1) Покажем, что`R Í (R-1 \R) È (`R Ç Rd). Пусть (x, y)Î`R, т.е. (x, y)ÏR. Для пары (y, x) возможны два случая: либо (y, x)ÎR, либо (y, x)ÏR. В первом случае получаем, что (x, y)ÎR–1 и (x, y)ÏR, следовательно, (x,y)Î R–1 \ R. Для второго случая спра-ведливо (x, y)Î`R и (x, y)Î R–1 = Rd, что означает (x, y)Î`RÇ Rd. В обоих случаях получим, что (x, y)Î (R-1 \ R) È (`R Ç Rd).
2). Докажем теперь обратное включение. Так как (x,y)Î Î(R–1 \ R) È (`R Ç Rd), то (x, y)Î R–1 \R или (x, y)Î`R Ç Rd. В обоих случаях то, что (x, y)`R следует непосредственно из определений пересечения или разности множеств.
Задача 15(г).
Решение. Пусть yÎrR°R, т.е. существует такой xÎA, что (x,y) Î
ÎR1oR2. Следовательно, найдется такое z, что (x,z)ÎR1 и (z,y)Î ÎR2, но это по определению означает, что z Î rRи zÎdR. Поэтому, zÎrRÇdR. Так как (z,y)Î R2, то по определению образа множества относительно отношения, получим yÎ R2(rRÇdR). R1d.
2) Докажем обратное. Пусть yÎ R2(rRÇdR), тогда существует элемент xÎrR°R, что (x,y) Î R2. Следовательно, xÎrRи xÎdRxÎrR следует, что найдется такой z, что (z,x) Î R1, а так как (x,y)Î R2, то (z,y) Î R1oR2. Поэтому yÎrR°R.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Доказать, что для любых множеств E, F, G справедливы равенства:
а) E´(F È G) = (E´F) È (E´G); б) E´(F Ç G) = (E´F) Ç (E´G);
в) (F È G)´E = (F´E) È (G´E); г) (FÇG)´E = (F´E) Ç (G´E).
2. Справедливы ли равенства:
а) (A´B) Ç (C´D) = (A Ç C) ´ (B Ç D);
б) (A´B) È (C´D) = (A È C) ´ (B È D)?
3. Доказать, что:
а) (A \ B)´C = (A´C) \ (B´C); б) A´(B \ C) = (A´B) \ (A´C).
4. Пусть множества A и C непусты. Доказать, что, для того чтобы A Í B и C Í D, необходимо и достаточно, чтобы вы-полнялось включение A´C Í B´D. Остается ли в силе это утвер-ждение, если A или C пусто?
5. Доказать, что если A Í P, B Í Q, то
A´B = (A´Q) Ç (B´P).
Доказать тождества (6-12).
6. (A Ç B) ´ (C Ç D) = (A´C) Ç (B´D).
7. (A È B) ´ (C È D) = (A´C) È (B´C) È (A´D) È (B´D).
8. A´B = (A´D) Ç (C´B), где A Í C и B Í D.
9. S2 \ (A´B) = [(S \ A) ´S] È [S´ (S \ B)].
10.Ç Аi´ Ç Bi= Ç(Аi ´ Bi).iÎI iÎI iÎI
11. È Аk´ ÈBt= È (Аk ´ Bt). kÎK tÎT (k,t)ÎK´T
12. Ç Аk´ ÇBt= Ç (Аk ´ Bt ).kÎK tÎT (k,t)ÎK´T
13. Пусть f: X®Y. Доказать, что отображение g: X® X´Y, определяемое равенством g(x) = (x, f(x)), инъективно.
14. Найти dR, rR, R –1, R o R, R o R –1, R –1 o R для отношений:
а) R = { (x, y) | x,yÎ N, x делит y };
б) R = { (x, y) | x, yÎ N, y делит x };
в) R = { (x, y) | x, yÎ R, x + y £ 0 };
г) R = { (x, y) | x, yÎ R, 2x ³ 3y };
д) R = { (x, y) | x, yÎ[–p/2; p/2], y ³ sin x };
е) R = { (x, y) | x, yÎ R, 9x2 £ 4y2 };
ж) R = { (x, y) | x, yÎ R, y2 – 4y + 5 < 2x };
з) R = { (x, y) | x, yÎ R, 4x2 – y2 £ 1 };
и) R = { (x, y) | x, yÎ R, xy < 3 };
к) R = { (x, y) | x, yÎ N, x – y делится на m };
л) R = { (x, y) | x, yÎ R, x – [x] = y – [y] };
м) R = { (x, y) | x, yÎ N, x и y имеют общий делитель };
н) R = { (x, y) | x, yÎ R, 4x2 + 9y2 < 36 }.
15. Доказать, что:
а) dR= Æ Û R=Æ Û rR = Æ; б) dR–1 =rR, rR–1=dR;
в) dR°R= R1-1 (rRÇdR); г) rR°R= R2(rRÇdR);
д) если B¹Æ то dA´B =A; е) если A¹Æ то rA´B=B.
16. Доказать, что R ¹ Rd для произвольного отношения R.
17. Доказать включение R–1Í RÈ(`R Ç R–1).
18. Доказать, что для любых бинарных отношений:
а) Qo(ÈRi) = È(Q o Ri); I ÎI i Î I б) Q o (Ç Ri) Í Ç(Q oRi); i ÎI i Î I
в) (ÈRi)oQ = È(Ri oQ); i ÎI i Î I г) (ÇRi)oQ Í Ç(RioQ). i ÎI i Î I
19. Доказать, что для того, чтобы отношение R Í A´B было взаимно однозначным соответствием между A и B, необходимо и достаточно, чтобы R o R–1 = R–1 o R = D.
20. Пусть X = {2, 3, 4, 5, 6, 7, 8, 9}. Построить матрицу и граф следующих бинарных отношений:
а) R = { (xi,xj) | xi,xjÎX, xi делится на xj };
б) R = { (xi,xj) | xi,xjÎX, xi >xj };
в) R = { (xi,xj) | xi,xjÎX, xi и xj имеют общий делитель};
г) R = { (xi,xj) | xi,xjÎX, xi ×xj £15};
д) R = { (xi,xj) | xi,xjÎX, $ n: xj =xi n }.
21. Для бинарных отношений R, определенных в задаче 15 п.1 построить множества GR(x) и HR(x).
22. Пусть x=(x1,x2) и R = { (x,y) |, x,yÎ R, r(x,y) £ k}. По-
строить верхний и нижний срезы отношения R, если:
а) r(x,y) =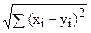 
; б) r(x,y) = max | xi - yi |; i i
в) r(x,y) = å| xi - yi |. I
