Свойства бинарных отношений

1) Рефлексивность.

Отношение R называется рефлексивным, если (х, х)ÎR для любого хÎA.

Примеры рефлексивных отношений: отношения "³", "£" на множестве R.

2) Антирефлексивность.

Отношение R называется антирефлексивным, если (х, х)ÏR для любого хÎA.

Примеры антирефлексивных отношений: отношения "<", ">" на множестве R.

Если R – антирефлексивное отношение, то xÏG_R(x) и хÏH_R(x) для любого хÎA.

3) Симметричность.

Отношение R называется симметричным, если для любых x, yÎA из того, что (x, y)ÎR следует (y, x)ÎR и обратно.

Примеры симметричных отношений: отношения "=" и "¹".

Если отношение R симметрично, то для любого хÎA

а) G_R(x) = H_R(x); б) R = R^–1.

4) Антисимметричность.

Отношение R называется антисимметричным, если для любых x и y из A из одновременного выполнения условий (x, y)ÎR и (y, x)ÎR следует, что x = y.

Отношение "³" также антисимметрично: если x ³ y и y ³ x, то x=y.

5) Асимметричность.

Отношение R асимметрично, если R Ç R^-1= Æ, т.е. пересечение отношения R с обратным отношением пусто.

Эквивалентное определение асимметричности: из двух отношений (x, y)ÎR и (y, x)ÎR одно не выполняется.

Примеры асимметричных отношений: ">", "<", "быть начальником".

Если R – асимметричное отношение, то из xRy следует y 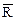x.

Для любого отношения R вводятся понятия симметричной части отношения R^s = R ÇR^-1 и асимметричной части отношения R^a = R \ R^s. Если отношение R симметрично, то R= R^s, если отношение R асимметрично, то R = R^a.

Примеры. Если R – "³", то R^–1 – "<", R^s – "=", R^a – ">".

6) Транзитивность.

Отношение R транзитивно, если для любыx x, y, zÎA из того, что (x, y)ÎR и (y, z)ÎR следует (x, z)ÎR.

Свойства транзитивного отношения:

а) RoR Í R;

б) для любого хÎA из yÎG_R(x) следует, что G_R(y) Í G_R(x).

Нетранзитивным является отношение "¹". Пусть x = 2, y = 3, z = 2, тогда справедливо x ¹ y и y ¹ z, но x = z, т.е. (x, z)ÏR.

Отношение R₁ называется транзитивным относительно отношения R₂, если:

а) из (x, y)Î R₁ и (y, x)Î R₂ следует, что (x, z)Î R₁;

б) из (x, y)Î R₂ и (y, x)Î R₁ следует, что (x, z)Î R₁.

7) Негатранзитивность.

Отношение R называется негатранзитивным, если`R транзитивно.

Примеры.

Отношения R₁ –">" и R₂ –" ¹" негатранзитивны, так как отношения`R<sub>1</sub> – "£",`R₂ – "=" транзитивны. Возможно одновременное выполнение свойств транзитивности и негатранзитивности. Например, отношение R₁ одновременно транзитивно и негатранзитивно, а R₂ , как известно, транзитивным не является.

8) Полнота.

Отношение R полно, если для любых x, yÎА либо (x, y)ÎR, либо (y, x)ÎR, либо оба отношения выполняются одновременно.

Свойства полных отношений:

а) G_R(x) È H_R(x) = А для любого хÎA;

б) полное отношение рефлексивно.

9) Слабая полнота.

Отношение R называется слабо полным, если для любых х ¹ y из А или (x, y)ÎR, или (y, x)ÎR.

Пример слабо полного отношения. Пусть А – множество предприятий, "неблагополучных" в смысле своего бюджета. Отношение R "быть должным" является слабо полным, так как каждое из этих предприятий или кому-либо должно, или ему кто-то должен, но быть должным самому себе нельэя и (x, x)ÏR.

10) Ацикличность.

Бинарное отношение R ациклично, если Rⁿ ÇR^–1= Æ для любого nÎ N. Иными словами, если из любой конечной цепочки отношений х₁Rx₂, x₂Rx₃,..., x_n-1Rx_n следует, что x₁¹х_n, то отношение R ациклично.

Задача 1. Доказать, что если отношения R₁, R₂ рефлексивны, то справедливо включение R₁ÈR₂ Í R₁oR₂ .

Решение. Пусть (x, y)ÎR₁ÈR₂, тогда (x, y)ÎR₁ или (x, y)ÎR₂. В первом случае из рефлексивности R₂ следует (y, y)ÎR₂ и, следовательно,(x, y)ÎR₁ o R₂. Аналогично для второго случая получим (x, x)ÎR₁ и (x, y)ÎR₁ o R₂, что и требовалось доказать.

Задача 2. Доказать, что отношение R негатранзитивно тогда и только тогда, когда R^d транзитивно.

Решение. Пусть отношение R негатранзитивно, т.е. если (x, y)ÏR и (y, z)ÏR, то (x, z)ÏR. Пусть для u, v, w выполнены условия (u, v)ÎR^d и (v, w)ÎR^d. Тогда, по определению двойственного отношения, (v, u)ÏR и (w, v)ÏR. Так как R негатранзитивно, то (w, u)ÏR, что означает (u, w)ÎR^d. Следовательно, R^d транзитивно.

Обратное следствие доказывается аналогично.

Задача 3. Доказать, что отношения R È (`R Ç R<sup>d</sup>) = R È (`R)^s полны.

Решение. Докажем равенство множеств, воспользовавшись свойствами операций над множествами и отношениями.

RÈ(`R Ç R<sup>d</sup> ) = R È (`R Ç ) = R È (`RÇ(`R)^-1) = R È (`R)^s.

Покажем теперь, что отношение R È (`R)<sup>s</sup> полно. Для любых x, yÎA возможен один из трех случаев: 1) (x, y)ÎR; 2) (y, x)ÎR; 3) (x, y)ÏR и (y, x)ÏR. В первых двух случаях принадлежность (x,y) к рассматриваемому отношению очевидна. Рассмотрим третий случай. Так как (x,y)Î`R и (x,y)Î 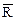^-1, то (x,y)Î(`R)^s. Следовательно, рассматриваемое отношение полно.

Задача 4. Доказать, что композиция эквивалентностей R₁ и R₂ является отношением эквивалентности тогда и только тогда, когда R₁ o R₂ = R₂ o R₁.

Решение. 1) Пусть R₁, R₂ и R₁ o R₂ - отношения эквивалентности. Докажем, что R₁ o R₂ = R₂ o R₁.

Пусть (x, y)ÎR₁ o R₂, так как R₁ o R₂ – отношение эквивалентности, то (y,x)ÎR₁ o R₂. Последнее означает, что существует такой элемент zÎA, что (y, z)ÎR₁ и (z, x)ÎR₂. Так как R₁ и R₂ – симметричны, то (x, z)ÎR₂ и (z, y)ÎR₁. Следовательно, (x, y)ÎR₂ o R₁. Обратное включение доказывается аналогично.

2) Пусть R₁ o R₂ = R₂ o R₁, покажем, что R₁ o R₂ является отношением эквивалентности.

Пусть x – произвольный элемент множества A. Так как R₁, R₂ рефлексивны, то (x, x)ÎR₁ и (x, x)ÎR₂, следовательно, (x,x)ÎR₁oR₂, т.е. отношение R₁ o R₂ – рефлексивно.

Докажем его симметричность. Пусть (x, y)ÎR₁oR₂, в силу равенства R₁ o R₂ = R₂ o R₁ получим (x, y)ÎR₂ o R₁, т.е. существует такой zÎA, что (x, z)ÎR₂, (z, y)ÎR₁. Из симметричности R₁ и R₂ следует, что (y, z)ÎR₁ и (z, x)ÎR₂. Следовательно, (y, x)ÎR₁ o R₂.

Для доказательства транзитивности достаточно показать, что (R₁ o R₂) o (R₁ o R₂) Í R₁ o R₂. Действительно,

(R₁ o R₂) o (R₁ o R₂) = R₁ o (R₂ o R₁) o R₂ = R₁ o (R₁ o R₂) o R₂ =

= (R₁ o R₁) o (R₂ o R₂) Í R₁ o R₂.

Задача 5. Пусть отображение j: A´A®A обладает свойствами:

а) j(x, y) = j(y, x);

б) j(x, j(y, z)) = j(j(x, y), z);

в) j(x, x) = x.

Доказать, что отношение R={ (x, y) | j(x, y) = x } является частичным порядком.

Решение. Проверим выполнение свойств отношения частичного порядка. Так как j(x, x) = x, то (x, x)ÎR и отношение рефлексивно.

Пусть выполнены оба условия (x, y)ÎR и (y, x)ÎR, т.е. j(x,y)=x и j(y, x) = y. Тогда x = y, так как j(x, y) = j(y, x) по определению функции j. Следовательно, отношение антисимметрично.

Докажем его транзитивность. Пусть (x, y)ÎR и (y, z)ÎR, т.е. j(x, y) = x и j(y, z) = y. Тогда

j(x, z) = j(j(x, y), z) = j(x, j(y, z)) = j(x, y) = x.

Следовательно, (x,z)ÎR, что и требовалось доказать.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Доказать, что если отношение R транзитивно, то R^–1 также является транзитивным.

2. Доказать, что из асимметричности отношения R следует асимметричность R^–1.

3. Доказать, что из антисимметричности отношения R следует антисимметричность R^–1.

4. Доказать, что из рефлексивности отношения R следует рефлексивность R ^–1.

5. Доказать, что для симметричности отношения R необходимо и достаточно, чтобы R^d было симметрично.

6. Отношение R симметрично тогда и только тогда, когда R = R^-1.

7. Доказать, что если отношения R₁ и R₂ рефлексивны, то рефлексивны отношения R₁ È R₂ , R₁ Ç R₂, R₁^–1.

8. Доказать, что если отношения R₁ и R₂ антирефлексивны, то антирефлексивны и отношения R₁ È R₂, R₁ Ç R₂, R₁^–1. Показать, что композиция R₁ o R₂ антирефлексивных отношений может не быть антирефлексивной.

9. Доказать, что если отношения R₁ и R₂ симметричны, то симметричныны отношения R₁ È R₂, R₁ Ç R₂, R₁^–1, R₁ o R₁^–1.

10. Доказать, что если отношения R₁ и R₂ антисимметричны, то антисимметричны также R₁ Ç R₂ и R₁^–1.

11. Пусть отношения R₁, R₂ – симметричны. Доказать, что для того чтобы R₁ o R₂ было симметрично необходимо и достаточно, чтобы выполнялось равенство R₁ o R₂ = R₂ o R₁.

12. Пусть отношения R₁ и R₂ антисимметричны. Объединение R₁È R₂ антисимметрично тогда и только тогда, когда R₁Ç R₂^-1 ÍD.

13. Доказать, что если отношение R асимметрично, то R Ç R₁ асимметрично для любого отношения R₁.

14. Доказать, что объединение R₁ÈR₂ асимметричных отношений R₁ и R₂ асимметрично тогда и только тогда, когда R₁ÇR₂^-1= = Æ.

15. Доказать, что если отношение транзитивно, то его симметричная и асимметричная части тоже транзитивны.

16. Пусть отношения R₁, R₂ транзитивны и R₁ транзитивно относительно R₂. Доказать, что тогда R₁ È R₂ также является транзитивным.

17. Какими свойствами должно обладать бинарное отношение R, чтобы выполнялось равенство R^–1 =`R?

18. Доказать, что отношение R асимметрично тогда и только тогда, когда R = (R^d)^a.

19. Доказать, что для того чтобы отношение R было полным необходимо и достаточно, чтобы выполнялось тождество

R^a= R^d.

20. Доказать, что если отношения R₁, R₂ рефлексивны, то их композиция тоже рефлексивна.

21. Доказать, что отношения R È (`R Ç R<sup>d</sup>) = R È (`R)^s полны.

22. Доказать, что если отношение R полно, то`R Ì R<sup>–1</sup> и R<sup>–1</sup> ==`R È (R Ç R^–1).

23. Доказать, что если отношение R асимметрично, то R^–1 Ì`R и`R = R^–1È(`RÇ R^d).

24. Доказать, что композиция полных отношений R₁ и R₂ является полным отношением.

25. Отношение Р негатранзитивно тогда и только тогда, когда xPy Þ " zÎА, xPz или zPy.

26. Доказать, что если R рефлексивно, то R^d антирефлексивно, если R антирефлексивно, то R^d рефлексивно.

27. Доказать, что полное отношение рефлексивно.

28. Доказать, что асимметричное отношение антирефлексивно.

29. Доказать, что отношение R негатранзитивно тогда и только тогда, когда R^d транзитивно.

30. Пусть отношение R симметрично, транзитивно и для любого x существует такой y, что (x, y)ÎR. Доказать, что оно рефлексивно.

31. Доказать, что ацикличное отношение асимметрично.

32. Доказать, что если отношение антирефлексивно и транзитивно, то оно ациклично.

33. Доказать, что асимметричное и негатранзитивное отношение транзитивно.

34. Доказать, что если отношение антирефлексивно, транзитивно и слабо полно, то оно негатранзитивно.

35. Доказать, что дополнение и двойственное отношение к антисимметричному и рефлексивному отношению R являются слабо полными.

36. Доказать, что любое отношение R симметричное и антисимметричное одновременно, является транзитивным.

37. Доказать, что для того чтобы отношение R было асимметричным необходимо, чтобы R^d и`R были полными.

38. Построить бинарное отношение:

а) рефлексивное, симметричное, не транзитивное;

б) рефлексивное, антисимметричное, не транзитивное;

в) рефлексивное, не симметричное, транзитивное;

г) не рефлексивное, антисимметричное, транзитивное;

д) симметричное, транзитивное, но не рефлексивное.

39. Доказать: а) I_уп È P_уп È P^–1 _уп = A´A;

б) I_уп = R^s_уп; P_уп = R^a_уп.

40. Доказать свойства 1), 2), 3), 6) отношения слабого порядка и производных от него отношений.

41. Доказать следующие свойства:

а) R_кач – полное негатранзитивное отношение;

б) отношение, не различающее близко расположенные точки

(т.е. xRy, если х ³ у – 1) является качественным порядком;

в) R_кач не является транзитивным, а, следовательно, R_кач ¹ R_сл ;

г) I_кач – рефлексивно, симметрично, но не всегда транзитивно;

д) I_кач = R^s_кач и R^d_кач = Р_кач.

42. Какие из следующих отношений являются отношениями эквивалентности:

а) равенства двух чисел;

б) подобия двух треугольников;

в) порядка на вещественной прямой;

г) линейной зависимости в пространстве Rⁿ (n > 1);

д) параллельности прямых на плоскости;

е) перпендикулярности прямых на плоскости.

43. Доказать, что если отношение R транзитивно и симметрично и d_R È r_R = A, то R – отношение эквивалентности.

44. Доказать, что композиция эквивалентностей R₁ и R₂ является отношением эквивалентности тогда и только тогда, когда R₁ o R₂ = R₂ o R₁.

Доказать, что R является отношением эквивалентности (45–49).

45. R = { (a, b) | a, bÎ N ´ N, a₁ + b₂ = b₁ + a₂}.

46. R = { (a, b) | a, bÎ N, a – b делится на m }.

47. R = { (a, b) | a, bÎ N ´ N, a₁b₂ = a₂b₁ , если a₂b₂ ¹ 0,

a₁= b₁, если a₂b₂ = 0 }.

48. R = { (a, b) | a, bÎ R, a – bÎ Q }.

49. R={ (x, y) | x, yÎ R, f(x) = f(y) }, функция f – фиксирована.

50. Доказать, что следующие отношения являются эквивалентностями. Построить для них фактор-множества.

а) R = { (x, y) | x, yÎ R ³, x₁² +x₂² +x₃² = y₁² +y₂² +y₃² };

б) R = { (x, y) | x, yÎ R ², x₁ = y₁ };

в) R = { (x, y) | x, yÎ R ² , x₂ = y₂ };

г) R = { (x, y) | x, yÎ R, x – [x] = y – [y] }.

51. Доказать, что R является отношением эквивалентности тогда и только тогда, когда (R o R^–1) È D = R.

51. Доказать, что если R – отношение эквивалентности, то и обратное отношение также является отношением эквивалентности.

52. Пусть R₁ и R₂ – отношения эквивалентности. Доказать, что

а) R₁ o R₁ = A² Û R₁ = A²;

б) R₁ o R₂ = A² Û R₂ o R₁ = A².

53. Доказать, что объединение R₁ È R₂ эквивалентностей R₁ и R₂ является эквивалентностью тогда и только тогда, когда R₁ È R₂ = R₁ o R₂.

54. Доказать, что отношение R на множестве A является одновременно эквивалентностью и частичным порядком в том и только в том случае, когда`R = D.

55. Показать, что следующие отношения являются частичным порядком:

а) A Ì B в универсальном множестве S;

б) x(t) £ y(t) для любого t в пространстве C[a,b];

в) m делит n на множестве N.

56. Пусть отображение j: A´A®A обладает свойствами:

а) j(x, y) = j(y, x);

б) j(x, j(y, z)) = j(j(x, y), z);

в) j(x, x) = x.

Доказать, что отношение R={ (x, y) | j(x, y) = x } является частичным порядком.

57. Пусть функции f₁ и f₂ определены на [0,1]. Будем говорить, что f₁Rf₂, если .

Показать, что R – отношение частичного порядка.

58. Пусть множества X, Y – частично упорядочены. Введем на X´Y отношение: (x₁, y₁) ³ (x₂, y₂), если x₁ ³ x₂, y₁ ³ y₂. Доказать, что это отношение является частичным порядком.

59. Доказать, что если R – частичный порядок, то R^-1 также частичный порядок.

60. Доказать, что отношение R на множестве A есть предпорядок тогда и только тогда, когда R = (R o R) È D.

Нечеткие множества.

Пусть Е – универсальное множество, x – элемент E, а Р – некоторое свойство. Обычное (четкое) подмножество A универсального множества E, элементы которого удовлетворяют свойству Р, определяется как множество упорядоченных пар A = {m_A(х) / х }, где m_A(х) – характеристическая функция, прини-мающая значение 1, если x удовлетворяет свойству Р, и 0 – в про-тивном случае.

Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа “да-нет” относительно свойства Р. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченных пар A = {m_A(х) /х}, где m_A(х) – характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве M (например, M = [ 0,1 ]). Функция принадлежности указывает степень (или уровень) принадлежности элемента x подмножеству A. Множество M называют множеством принадлежностей. Если M = { 0,1 }, то нечеткое подмножество A может рассматриваться как обычное или четкое множество.