СЛУЧАЙНЫЕ СОБЫТИЯ
Классическое определение вероятности  , где п – общее количество всех возможных исходов опыта, а m – количество тех исходов, при которых наступает событие А (благоприятствующих событию А).
, где п – общее количество всех возможных исходов опыта, а m – количество тех исходов, при которых наступает событие А (благоприятствующих событию А).
Элементы комбинаторики
1) если множество из l элементов перемешивается (элементы множества меняются местами), то речь идёт о перестановках, количество которых равно 
2) если из множества l элементов берётся k элементов, то получаются:
а) сочетания, когда порядок следования элементов не важен, общее количество которых равно  ;
;
б) размещения, когда порядок следования элементов важен, общее количество которых равно  .
.
Алгебра событий

1) 
 А или В
А или В 

 А и В несовместны, тогда
А и В несовместны, тогда 
Если 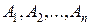 попарно несовместны (т.е.
попарно несовместны (т.е.  ), то
), то


2) 
 А и В (одновременно)
А и В (одновременно)  , где
, где  – условная вероятность события В при условии, что событие А произошло.
– условная вероятность события В при условии, что событие А произошло.
 Если
Если  , то А и В – независимые события.
, то А и В – независимые события.
Если 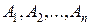 попарно независимы, то
попарно независимы, то

3) 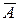
 не А (противоположное событию А)
не А (противоположное событию А)
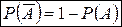
Полная вероятность
Если эксперимент состоит из нескольких этапов, требуется найти вероятность события, произошедшего на последнем этапе, а о результатах промежуточных этапов мы можем строить лишь предположения (гипотезы), то пользуются формулой полной вероятности:
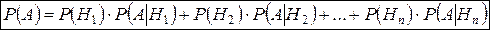 ,
,
где  – полная группа гипотез: 1)
– полная группа гипотез: 1)  ;
;
2) 
Если событие на последнем этапе представлено как свершившийся факт, а требуется найти вероятность того, что вместе с событием А осуществилась одна из гипотез  , то пользуются формулой Байеса:
, то пользуются формулой Байеса:
 ,
,
где  – полная вероятность события А.
– полная вероятность события А.
Схема Бернулли (схема повторных независимых испытаний)
Если один и тот же эксперимент в одних и тех же условиях проводится п раз (несколько раз), причём результаты испытаний не зависят друг от друга, то мы находимся в рамках схемы Бернулли.
Пусть А – случайное событие, происходящее при одном испытании,  ,
, 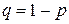 .
.
1) Если требуется найти вероятность того, что в п испытаниях событие А произошло ровно m раз (говорят: «произошло m успехов»), то применяют:
а) Формулу Бернулли 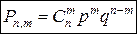 , единственную формулу, дающую точный ответ.
, единственную формулу, дающую точный ответ.
Для больших п применяют предельные теоремы, дающие ответ приближенно:
б) Локальную теорему Муавра-Лапласа  , где
, где  – функция Гаусса (значения по таблице),
– функция Гаусса (значения по таблице),  .
.
в) Теорему Пуассона  , где
, где  – порядка единиц (
– порядка единиц ( ).
).
2) Если требуется найти вероятность того, что в п испытаниях событие А произошло от  до
до  раз, то применяют интегральную теорему Муавра-Лапласа
раз, то применяют интегральную теорему Муавра-Лапласа 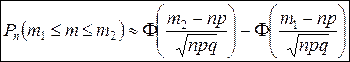 , где
, где  – интеграл Лапласа (значения по таблице),
– интеграл Лапласа (значения по таблице),  ,
,  .
.
3)  – наивероятнейшее количество наступлений события А в п испытаниях вычисляется из формулы:
– наивероятнейшее количество наступлений события А в п испытаниях вычисляется из формулы:  , где
, где  может быть одним целым числом, в случае, если концы интервала дробные (единственное целое число на интервале длиной единица), и двумя целыми числами, если концы интервала целые.
может быть одним целым числом, в случае, если концы интервала дробные (единственное целое число на интервале длиной единица), и двумя целыми числами, если концы интервала целые.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайной величиной называется функция, определённая на пространстве элементарных событий  , которая ставит в соответствие каждому элементарному событию из
, которая ставит в соответствие каждому элементарному событию из  некоторое действительное число (любое, следующее из условия задачи)
некоторое действительное число (любое, следующее из условия задачи)  .
.
Случайные величины (с.в.) делятся на дискретные и непрерывные. И те и другие обладают функцией распределения: функцией, определённой на всей числовой оси R, значения которой равны вероятности того, что случайная величина примет значения, строго меньшие аргумента функции
 .
.
Свойства функции распределения:
1.  ;
2. ;
2.  ;
3. ;
3.  , ,  ;
4. ;
4. 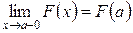 (непрерывность слева); (непрерывность слева);
| 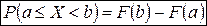 ; ;
 . .
|
Числовые характеристики случайных величин
С.в. обладают: математическим ожиданием  (математическим средним), демонстрирующим, какое в среднем значение должна принять случайная величина (зависящее от возможных значений случайной величины и соответствующих им вероятностей); дисперсией
(математическим средним), демонстрирующим, какое в среднем значение должна принять случайная величина (зависящее от возможных значений случайной величины и соответствующих им вероятностей); дисперсией 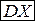 , показывающей степень рассеянности значений случайной величины от её математического ожидания (дисперсия равна мат.ожиданию квадрата отклонения значения случайной величины от её математического ожидания
, показывающей степень рассеянности значений случайной величины от её математического ожидания (дисперсия равна мат.ожиданию квадрата отклонения значения случайной величины от её математического ожидания  ), вычислительная формула –
), вычислительная формула –  , а также среднеквадратическим отклонением
, а также среднеквадратическим отклонением  , показывающим то же, что и дисперсия, но в других единицах.
, показывающим то же, что и дисперсия, но в других единицах.
Свойства математических ожиданий и дисперсий
 ,
,  ,
,  , где С=const.
, где С=const.
 ,
, 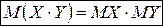 – верно для независимых Х и Y.
– верно для независимых Х и Y.
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
(принимающие конкретные значения)
обладают законом (рядом) распределения – таблицей из двух строк: в верхней отражаются упорядоченные по возрастанию значения случайной величины, в нижней – вероятности, с которыми случайная величина принимает эти значения.
| Х | 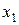
| 
| … | 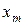
|
| Р | 
| 
| … | 
|
где  .
.
Функция распределения для этих величин кусочно-непрерывная, график её представляет собой участки прямых параллельных оси Ох, образующих ступени, поднимающиеся от 0 до 1.
Математическое ожидание дискретной случайной величины определяется по формуле:  ,
,
а её дисперсия:  .
.
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
(принимающие значения на интервале, например временном промежутке)
обладают плотностью распределения (вместо закона распределения у дискретных с.в.), которая является некоторой неотрицательной функцией, определённой на всей числовой прямой, обладающей свойством  .
.
Связь с функцией распределения:  , а
, а  .
.
Функция распределения непрерывных с.в. непрерывна.
Математическое ожидание непрерывной случайной величины находится по формуле:  , а её дисперсия:
, а её дисперсия:  .
.
СТАНДАРТНЫЕ РАСПРЕДЕЛЕНИЯ
Для дискретных случайных величин:
1. Биномиальное распределение – когда вероятности в законе распределения находятся по формуле Бернулли  :
:
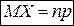 ,
, 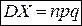 .
.
2. Распределение Пуассона – когда вероятности в законе распределения находятся по теореме Пуассона  , где
, где 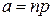 :
:
 ,
, 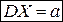 .
.
3. Геометрическое распределение – когда вероятности в законе распределения находятся по формуле  :
:
 ,
,  .
.
Для непрерывных случайных величин:
4. Равномерное распределение на промежутке 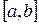 (с параметрами a и b):
(с параметрами a и b):
 ,
,  ,
,  ,
,
 ,
,  .
.
5. Показательное распределение с параметром  :
:
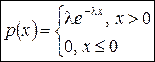 ,
,  ,
, 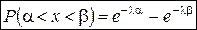 ,
,  ,
,
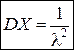 .
.
6. Нормальное распределение с параметрами а и 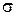 :
:
 ,
,  ,
,
 ,
, 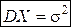 ,
,
 ,
,  ,
,
Правило трёх сигм:  .
.






