Допустимые управления
От значительной части недостатков классического вариационного исчисления, возникающих при решении задач с ограниченными управлениями и ограниченными фазовыми координатами, свободен метод, разработанный академиком Л.С.Понтрягиным в 1956-1961 гг. и называемый принципом максимума. Принцип максимума до настоящего времени остается основным инструментом для определения оптимального управления и оптимальных траекторий.
Теоремы принципа максимума относятся к системам, поведение которых можно описать дифференциальными уравнениями:
(9.75) (9.59)
или векторным уравнением
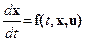
где х = (х 1, х 2,…, хn) – координаты объекта управления (фазовые координаты) и f = (f 1, f 2,…, fn) – n -мерные векторы, а u = (u 1, u 2,…, um) – управления (управляющие воздействия), причем производные от управлений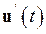 
в уравнения (9.75) не входят, t – время.
Будем считать, что вектор управления может принимать свои значения из некоторого множества U. U может быть любым множеством m -мерного евклидового пространства, например оно может состоять из совокупности изолированных точек.
Будем предполагать, что в уравнениях (9.75) функции fi (i = 1: n) непрерывны по всем своим переменным и непрерывно дифференцируемы по переменным хj (j = 1: n).
Каждое из управлений u 1,…, um непрерывно для всех рассматриваемых t, за исключением конечного числа моментов, где они могут претерпевать разрывы первого рода (рис. 9.24). Такие управления называются кусочно-непрерывными и они удовлетворяют условию u (t)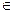 
U.
Рис. 9.24. Форма допустимых управляющих воздействий
Управляющие воздействия могут иметь различный физический характер (напряжение, расход топлива, положение «руля» и т.п.) и реализоваться различными техническими средствами.
Векторное пространство с декартовыми координатами х 1, х 2,…, хn будем называть фазовым пространством системы (9.75) и обозначать Х. Каждому вектору х в фазовом пространстве соответствует некоторая точка (фазовая точка). Если задан вектор u (t) и начальное условие x (t 0) = x 0 = (
), то систему уравнений (9.75) можно решить. Разным вектор-функциям u (t) будут соответствовать различные решения x (t) уравнений (9.75), т.е. выбором вектора u (t) можно управлять движением системы. Решению x (t), t 0 ≤ t ≤ t 1, в фазовом пространстве Х соответствует некоторая линия, которая называется фазовой траекторией системы.
Предполагается, что на участках непрерывности и в точках разрыва управления могут принимать лишь конечные значения, причем на каждое из управлений могут накладываться дополнительные ограничения вида
(9.76)
или в более общем случае
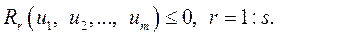(9.77)
Ограничения вида (9.76) и (9.77) образуют в пространстве управлений некоторую область допустимых значений управляющих воздействий. В этой области управление u может изменяться монотонно или скачком переходить из одной точки в другую конечное число раз. Управления с бесконечно большим числом переключений считаются недопустимыми (нереализуемыми). Тем не менее, при использовании принципа максимума можно получить оптимальные траектории, для точной реализации которых потребуется бесконечно большая частота переключения управляющего воздействия. В таких случаях ее реализуют приближенно при конечной частоте переключения управляющего воздействия. Движение вдоль таких траекторий, как указано выше, называют скользящим режимом.
Управляющие воздействия в излагаемой формулировке принципа максимума должны быть свободными (независимыми) в том смысле, что нельзя задаваться фиксированным числом разрывов (переключений) или жестко привязывать какие-либо из них к времени и фазовым координатам системы. Таким образом, требование кусочной непрерывности определяет лишь класс допустимых управлений, а не конкретную их форму.
Необходимо отметить, что в отличие от обычных задач вариационного исчисления, где все искомые функции были равноправны, в принципе максимума разделяются фазовые координаты xi и управления. Это разделение удобно в тех случаях, когда ограничения накладываются только на управления, а не на фазовые координаты, т.к. не любые точки фазового пространства являются достижимыми. Бессмысленно, например, требовать, чтобы при напряжении возбуждения двигателя, ограниченного условием 
, ток возбуждения двигателя за ограниченное время поднялся до единичного значения. Тем более бессмысленно требовать, чтобы ток возбуждения достигал когда-либо значения, большего единицы. В общем случае каждой начальной точке фазового пространства соответствует некоторая область достижимых значений и, наоборот, область, из которой можно попасть в данную точку. Это следует учитывать при постановке задач и не требовать перевода изображающей точки в недостижимую область.
