ТЕОРИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Определения
На рис. 9.1. показана общая структурная схема управления, состоящая из двух звеньев 1 и 2. Звено 1 называется управляющим органом или управляющим устройством. Оно должно прежде всего обеспечивать цель управления. Звено 2 называется объектом управления. Под термином «объект управления» будем понимать не только машины и механизмы, но и целые производственные процессы.
Рис. 9.1. Структурная схема системы управления
Задачу оптимального управления можно представить в виде составного объекта (рис. 1.1): цель управления, управляемый объект, измерительную систему и вычислительное устройство, осуществляющее расчет оптимального управления.
Задача вычислительного устройства – найти связи между вектором состояния в конечный момент времени х к, вектором управления u и измеренным вектором состояния х изм.
При решении задачи оптимизации необходимо вначале выбрать и сформулировать цель (выбрать критерий оптимальности), затем согласовать ее с имеющимися возможностями (учесть ограничения) и, наконец, реализовать способ достижения цели при учете ограничений.
Предполагается, что состояние исследуемого объекта управления в каждый момент времени t на отрезке 
однозначно характеризует n действительными числами x 1(t), x 2(t),…, xn (t) или вектор – функцией x (t)= (x 1,…, xn) в пространстве En, которое будем называть фазовым пространством или пространством состояний объекта. Изменение вектора состояния во времени будем называть движением объекта в (n +1)–мерном пространстве позиций 
. Составляющие вектора x могут иметь самую различную природу и сущность: для генератора − напряжение, мощность и частота; для предприятия − отдельные показатели плана. На составляющие вектора х могут и почти всегда накладываются ограничения типа
х 1≤ Х 1, х 2≤ Х 2,…, хn ≤ Хn.
Допустим, мощности всех машин, аппаратов, предприятий и даже целой страны на некотором отрезке времени всегда ограничены. Нарушение этих ограничений обычно приводит к ненормальным и опасным режимам.
К объекту управления приложены воздействия: управляющие, которые могут быть охарактеризованы некоторой вектор – функцией u (t) = (u 1, u 2,…, uk), называемой управлением, и возмущающие, представляемые вектор –функцией z (t) = (z 1, z 2,…, zl).
Управляющие воздействия − это воздействия, которые сознательно меняются для достижения цели управления. На составляющие вектора u накладываются ограничения типа
u 1≤ U 1, u 2≤ U 2,…, uk ≤ Uk.
Если взять синхронный генератор, то напряжение возбуждения, с помощью которого управляют напряжением на статоре, не может превосходить паспортных данных.
Управляющий орган характеризуется прежде всего способностью вырабатывать вектор u. Изменение вектора u во времени или в пространстве координат (u 1, u 2,…, uk) называется алгоритмом управления. Таким образом, управляющее устройство выдает на объект управления алгоритм в виде изменения вектора u. В свою очередь устройство управления получает внешние команды y, служащие для запуска и перестройки управляющего устройства.
На объект управления могут также действовать возмущающие воздействия, которые, как правило, искажают алгоритм управления u, мешают достижению цели управления, поэтому они называются часто помехами.
Некоторые составляющие вектора z могут быть полезными, т.е. такими, для преодоления которых и предназначен объект, например преодоление полезного момента двигателем. Возмущающие воздействия в большинстве случаев не подвластны человеку и зачастую можно говорить о характере их изменения только в статистическом смысле.
Если детально изучить составляющие вектора z, то, очевидно, найдутся ограничения типа выше указанных.
Векторы x, u, z связаны обычно некоторой закономерностью. Рассматриваются только такие объекты, в которых связь между векторами может быть записана в виде системы обыкновенных дифференциальных уравнений
(9.1)
или в векторной форме
где функции fi определены для любых значений х, принадлежащих некоторой области х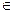 
Х, и любых значений u, принадлежащих области управления u 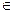U. Области X и U могут быть открытыми и замкнутыми. Функции fi непрерывны по совокупности x 1, x 2,…, xn и непрерывно дифференцируемы по x 1, x 2,…, xn. Вектор u может быть функцией непрерывной, кусочно-непрерывной или кусочно-гладкой.
Управляющее устройство может получать информацию о векторах x и z и на основе этого формировать вектор u, а может и не получать никакой информации об объекте управления. В первом случае имеется замкнутая система управления, во втором − разомкнутая. В технике нашли применение оба вида систем, но замкнутые распространены гораздо больше. Разомкнутые системы работают по жесткому алгоритму, т.е. являются системами детерминированными. В замкнутых системах алгоритм может меняться в зависимости от значений векторов x и z. Такие системы иногда называются информационными.
Охарактеризовав систему автоматического управления (САУ), следует определить цель управления, т.е. ради чего создается система управления.
В самом общем виде цель управления определяется некоторым функционалом
(9.2)
где G 0 − некоторая ограниченная область пространства позиций; t 0 − начальный момент времени. Требуется найти такой алгоритм u (t) или u = f (x, z), при котором функционал (9.2) принимал бы экстремальное значение, т.е.
При определении функционала, естественно, должны учитываться ограничения, накладываемые на u, z:
z (t) 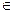Z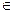, u (t) U, t 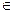T, (9.3)
отражающие особенности задачи. В частном случае, это могут быть ограничения отклонения рулей, энергетических режимов, ограничения на допустимые условия эксплуатации системы и т.д.
Стратегия управления
Для выбора управления u (t)в общем случае может использоваться любая доступная исследователю к моменту t информация. Способ формирования управляющих воздействий будем в дальнейшем обозначать U и называть стратегией, а его реализацию − законом управления.
В зависимости от того, какая информация используется для формирования управляющих воздействий, можно выделить три существенно различных типа стратегий.
I. Начнем с простейшего случая, когда управление u выбирается заранее сразу на весь отрезок времени Т и в процессе движения не корректируется. Такое управление называется программным, а соответствующие программные стратегии U = u представляют собой функции времени, которые в дальнейшем будем полагать кусочно-непрерывными.
II. Рассмотрим теперь второй случай, когда в процессе движения непрерывно измеряется состояние объекта, так что в каждый момент времени известна сложившаяся позиция [ t, x (t)]. Позиционная стратегия U выбирает текущее значение управления в зависимости от сложившейся позиции, u (t) = U [ t, x (t)], иначе говоря, позиционное управление формируется по принципу обратной связи в зависимости от состояния объекта. Совокупность всех функций U | u (t) = U [ t, x 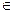(t)] P, t 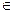T, назовем множеством позиционных стратегий и будем обозначать U x.
III. При использовании позиционных стратегий, не стесненных никакими дополнительными ограничениями, следует иметь в виду одну существенную особенность. Если функция U [ t, x (t)] разрывна по х (именно такие функции чаще всего оказываются самыми эффективными), то в системе управления могут возникнуть так называемые скользящие режимы. При этом решение уравнения (9.2) в классическом смысле не существует.
В зависимости от назначения рабочего механизма могут ставиться самые различные задачи управления. Наиболее распространены следующие режимы управления механизмами:
1) Рабочий механизм должен переместиться из одного положения в другое (позиционное перемещение).
2) Рабочий механизм должен за минимальное время разогнаться до заданной скорости или затормозиться.
3) Совершить заданную работу за минимальное время.
В том случае, когда можно пренебречь ограничением по нагреву, задачу оптимального управления можно сформулировать следующим образом: требуется отработать заданное перемещение (перейти от одной скорости к другой или совершить заданную работу) за минимальное время при наличии ограничений на ток якорной цепи, скорость и управляющие воздействия на цепи возбуждения генератора и двигателя.
При решении задачи оптимального по быстродействию управления с учетом нагрева двигателя можно потребовать, чтобы потери энергии в якорной цепи за время работы привода не превышали допустимых.
В этом случае задача может быть сформулирована следующим образом: требуется отработать заданное перемещение (перейти от одной скорости к другой или совершить заданную работу) за минимальное время при наличии ограничения на ток, скорость и управляющие воздействия при условии, что потери (или среднеквадратичный ток) за время работы привода не будут превышать заданного значения.
Уравнение Эйлера
Переходим к основному вопросу вариационного исчисления — выводу необходимых условий экстремума (для определенности минимума). Мы будем исследовать, каким условиям должна удовлетворять функция у (х) для того, чтобы при переходе от нее к любой функции 
(х) приращение функционала было положительным. Именно эти условия позволят нам впоследствии находить искомые функции, доставляющие экстремум функционалам.
Дифференциальное уравнения второго порядка
= 0 (9.10)
или
(9.10')
В многомерном случае основная задача вариационного исчисления записывается в виде системы n уравнений:
i =1: n. (9.10'')
Уравнение (9.10) называется уравнением Эйлера. Оно было найдено Эйлером в 1744г. и играет центральную роль в вариационном исчислении.
Решения уравнения Эйлера называются экстремалями. Только на экстремалях может достигаться экстремум функционала.
Уравнение Эйлера является только необходимым, но не достаточным условием экстремума. Оно не дает гарантии того, что на экстремали действительно достигается экстремум (подобно тому, как в дифференциальном исчислении точки, где y ' = 0, не обязательно доставляют экстремум функции y (t)).
Таким образом, с помощью уравнения Эйлера можно фактически определить функцию, на которой может достигаться экстремум, но не всякое решение уравнения Эйлера является решением поставленной вариационной задачи.
Пример 9.1. Определить функцию, на которой может достигаться экстремум функционала
при граничных (краевых) условиях
y (0) = 0, y (1) = 1.
Решение. В рассматриваемом примере F = y 2 + y '2, поэтому
В результате уравнение Эйлера будет иметь вид
y '' – y = 0.
Решение полученного уравнения ищем в виде y = erx. В результате получаем уравнение r 2 – 1 = 0. Откуда r = ± 1, r 1 = 1, r 2 = -1.
В общем виде решение уравнения Эйлера имеет вид
y (х) = С 1 er 1 x + С 2 er 2 x
или
y (х) = С 1 ex + С 2 e-х.
Из граничных условий получаем
Откуда
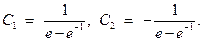
Окончательно, экстремаль имеет вид
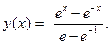
Динамическое программирование
В теории управления для оптимизации функционалов при наличии ограничений на векторы управления и состояния применяют принцип максимума и метод динамического программирования, разработанные в 1956…1957 годах российским и американским математиками Л.С.Понтрягиным и Р. Беллманом на основе классических методов вариационного исчисления Эйлера, Лагранжа.
Динамическое программирование является методом решения задач оптимального управления для замкнутых областей. Оно отличается как от классических вариационных методов, так и от принципа максимума, хотя и находится с ним в тесной связи.
В основе динамического программирования лежит следующий «принцип оптимальности», предложенный Р. Беллманом в качестве гипотезы: оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальное состояние и решение (управление) и начальный момент, последующие решения (управления) должны составлять оптимальное поведение относительно состояния, получившегося в результате первого решения.
Доказательства этот принцип, по существу, не требует. Ведь если какой-то участок траектории (рис. 9.16) можно улучшить, оставляя неподвижными его концы (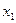
и 
), то и вся траектория не может быть оптимальной, так как траектория х 1, …, хi,...,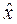 
,...., хn +1 окажется лучше.
Рис. 9.16. К пояснению принципа оптимальности
На основании принципа оптимальности исходная задача об оптимальном попадании в состояние хn +1 из заданного состояния х 0 может быть погружена в класс задач о попадании в состояние хn +1 из любого допустимого промежуточного состояния. На первый взгляд замена конкретной задачи целым классом задач того же типа сильно усложняет решение. В действительности, как это будет показано ниже, это не совсем так.
Следует иметь в виду, что теория динамического программирования разрабатывалась Р. Беллманом для более обширного класса процессов, чем процессы, описываемые системами обыкновенных дифференциальных уравнений. Поэтому Р. Беллман и опирался на столь общий принцип, как принцип оптимальности. В столь общей форме, как высказанная выше, принцип оптимальности не доказан, но для систем, описываемых дифференциальными уравнениями, справедливость его следует из того простого факта, что каждый отрезок экстремали есть тоже экстремаль и всякий участок оптимального управления также является оптимальным управлением.
Исходя из принципа оптимальности, Р. Беллман вывел дифференциальное уравнение в частных производных, позволяющее определить кривые, на которых достигается экстремум.
Рассмотрим автономную систему, движение которой описывается уравнениями
, i =1: n, (9.49)
где хi — фазовые координаты системы, а u — функция управления, принимающая значения в некоторой допустимой области.
Пусть требуется для системы (9.49) найти такое допустимое управление, что при движении системы из заданной начальной точки xi (t 0), i = l, 2,..., n в начало координат достигается минимум следующего функционала:
J (u) = 
(9.50)
Введем в рассмотрение функцию
, (9.51)
называемую функцией Беллмана, предполагая, что она всюду, за исключением концов фазовой траектории, имеет непрерывные частные производные 
; i = 1: n.
Тогда оптимальное управление u, доставляющее минимум функционалу (9.50), должно удовлетворять следующему уравнению:
. (9.52)
В уравнение Беллмана (9.52), помимо неизвестной функции V, входит еще и неизвестная функция управления u. Используя требование минимизации выражения, стоящего в прямых скобках уравнения (9.52), последнее можно свести к следующей теме:
(9.53)
Одно из этих уравнений можно использовать для исключения величины u. При этом управление u будет выражаться через x и 
:
. (9.54)
Общая идея приближенных алгоритмов, основанных на принципе оптимальности, заключается в том, что весь интервал, на котором нужно оптимизировать процесс, делят на такое число малых интервалов, чтобы решение задачи оптимизации на этом малом интервале было уже несложным. После этого решение задачи начинается «с конца». Как было указано выше согласно принципу оптимальности, оптимальное управление на последнем шаге не зависит от того, каким было управление на предыдущих шагах. На последнем шаге управление должно быть, во-первых, оптимальным для условий данного (и только данного) шага и, во-вторых, приводить в заданную конечную точку.
Однако для выбора управления на последнем шаге нужно знать, чем кончился предпоследний. Это даст начальное условие для последнего шага. Поскольку мы его не знаем, будем делать разные предположения об исходе предпоследнего шага и для каждого из этих предположений вычислять оптимальное управление и значение функционала на последнем шаге. После этого переходим к выбору управления на предпоследнем шаге, причем его выбираем так, чтобы оно совместно с уже выбранным управлением на последнем шаге обеспечивало экстремум функционала на двух последних шагах. Таким образом, процесс динамического программирования развивается в обратном по времени направлении — от конца к началу — до тех пор, пока не доходит до заданной начальной точки.
Характерные особенности алгоритмов динамического программирования удобно рассматривать на примере дискретной задачи. Представим себе прямоугольное поле из m·n клеток: m — по горизонтали и n — по вертикали. На рис. 9.17 для наглядности показано поле при m = 5 и n = 4. Пусть для каждой клетки задана «стоимость» перехода в любую клетку соседнего справа столбца. Требуется найти оптимальную по стоимости траекторию перехода из заданной клетки крайнего левого столбца в заданную клетку крайнего правого столбца. Если искать оптимальный путь простым перебором, то придется сравнивать между собой 
возможных путей, а это очень большое число. При больших n и m прямой перебор нереален.
Рис. 9.17. Иллюстрация оптимальной траектории
Рассмотрим теперь, что может в этой ситуации дать динамическое программирование. Пусть заданной конечной клеткой является клетка 52. На последнем шаге в эту клетку можно попасть из клеток 41, 42,... 44. Запишем стоимости перехода из каждой из этих клеток в клетку 52 как характеристики клеток (на рис. 56 характеристики указаны в кружках), после чего перейдем к выбору решения на предпоследнем шаге. Из клетки 31 можно перейти в любую из клеток четвертого столбца, а из нее — в клетку 52, всего возможны четыре пути. Сравним их между собой и выберем путь с наименьшей стоимостью (с учетом стоимости движения из клетки четвертого столбца в конечную клетку 52). Стоимость перехода в клетку 52 по наилучшему пути запишем как характеристику клетки 31. Повторим эту процедуру для каждой из клеток третьего столбца. На рис. 9.15 выписаны характеристики всех клеток третьего столбца и для каждой клетки показан оптимальный путь. Переходя теперь ко второму столбцу, убеждаемся, что для каждой из клеток этого столбца нужно сравнить между собой только четыре варианта пути. Действительно, если, например, находясь в клетке 21, мы избрали путь в клетку 31, то над дальнейшим выбором пути задумываться уже не надо — оптимальный путь из клетки 31 был определен на предыдущем шаге исследования, а согласно принципу оптимальности, этот путь не зависит от того, каким образом мы попали в клетку 31. Заполнив характеристики клеток второго столбца, переходим к последнему шагу решения — складываем стоимости перехода из заданной клетки 13 с характеристиками клеток второго столбца и выбираем наименьшую из сумм. Пусть наименьшая сумма соответствует переходу в клетку 21. Тогда оптимальной траекторией (рис. 9.15) будет последовательность 13—21—31—41—52.
Подсчитаем теперь, сколько сравнений возможных путей необходимо провести при решении общей задачи выбора траектории на поле из m · n клеток. В каждом из столбцов, кроме крайних, необходимо сделать n 2 сравнений путей (по n путей в каждой из n клеток), в крайних столбцах — по n сравнений, т. е. всего будет 
сравнений, а это гораздо меньше, чем путей при прямом переборе. Так, при n = m = 10 при прямом переборе надо сравнить 10 000 000 путей, а при использовании динамического программирования — 820. В сокращении числа кривых сравнения заключается основное достоинство алгоритмов, основанных на идеях динамического программирования.
