Анықтама. Егер n-реттті алмастыруды бірінің астына бірін жазсақ, n-ретті қойылым шығады.
 =
= 
47. Анықтауыштың негізгі қасиеттері. (дәлелдеумен)
1)Егер анықтауышта екі жолдың(бағанның) орындарын ауыстырсақ онда анықтауыштың таңбасы қарама-қарсыға ауысады.
Дәлелдеу.  =
= 
2)Егер матрицаны аударсақ онда оның анықтауышы өзгермейді:|  |=|A|
|=|A|
3)Егер анықтауыштың бір жолының(бағанының) ортақ көбейткіші бар болса,онда оны анықтауыштың таңбасының сыртына шығаруға болады.
Дәлелдеу.
 =a
=a 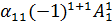 +a
+a  +…a
+…a  =a|A|
=a|A|
4)Егер матрицаның қандай да бір жолына(бағанына) басқа жолды (бағанды) санға көбейтіп алып қоссақ, онда анықтауыш өзгермейді
5)Егер анықтауыштың екі жолы(бағаны) бірдей болса, онда анықтауыш нөлге тең болады.
6)Блокты үшбұрышты матрицалардың анықтауышы диагональдік блоктарының анықтауыштарының көбейтіндісіне тең болады.
7)Егер А матрицасының жолдары немесе бағандары сызықтық тәуелді болса, онда анықтауыш 0-ге тең.
Сызықтық кеңістіктің анықтамасы. Мысалдар. Сызықтық кеңістіктердің базисы және өлшемі. Сызықтық кеңістіктердің өлшемі туралы теорема.
(P, +, *) P өрісі берілген (X,  ,
,  ) веторлар жиыны берілсін,
) веторлар жиыны берілсін,  ,
,  <= қосу; санға көбейту векторлардын.<X,P> жұбы сызықтық кеністік деп аталады, егер төмендегі аксиомалар орындалса:
<= қосу; санға көбейту векторлардын.<X,P> жұбы сызықтық кеністік деп аталады, егер төмендегі аксиомалар орындалса:
1.  x,y
x,y  X x
X x  y= y
y= y  x
x
2.  x,y,z
x,y,z  X (x
X (x  y)
y)  z = x
z = x  (y
(y  z)
z)
3.  x
x  X
X 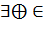 X x
X x  y= y
y= y  x=
x= 
4.  x
x  X
X  y
y  X x
X x  y= y
y= y  x=
x= 
5.  x
x  X 1
X 1 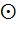 x=x
x=x
6.  P
P  x
x  X (
X ( )
) 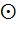 x=
x=  (
( )
)
7.  P
P  x
x  X (
X ( )
) 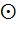 x=
x=  x
x  x
x
 P
P  x,y
x,y  X
X  (x
(x  y)=
y)=  x
x  yМысалы: 1. (Mn*k (
yМысалы: 1. (Mn*k (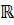 ),t,*) – сызықтық кеңістік; 2. (М1*n
),t,*) – сызықтық кеңістік; 2. (М1*n  n)- сызықтық кеңістік. <X,P> сызықтық кеністік а1,a2,a3,…,ak
n)- сызықтық кеңістік. <X,P> сызықтық кеністік а1,a2,a3,…,ak  XL(а1,a2,a 3,…,ak )={
XL(а1,a2,a 3,…,ak )={  +
+  +…
+… 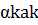 / α1,α2,αk
/ α1,α2,αk  P}-бұл сызықтық қабықша(a1…ak), {b1…bn} векторлар жуйесинің сызықтық эквиваленті деп аталады. Келесі шарттар орындалса: 1.
P}-бұл сызықтық қабықша(a1…ak), {b1…bn} векторлар жуйесинің сызықтық эквиваленті деп аталады. Келесі шарттар орындалса: 1.  i ai
i ai  L{b1…bn} 2.
L{b1…bn} 2.  j aj
j aj  L(a1…an)a1,a2…ak сызықтық векторлар базисі деп аталады егер келесі 2 шарт орындалса:1.{a1…ak} сызықтық тәуелсіз 2.
L(a1…an)a1,a2…ak сызықтық векторлар базисі деп аталады егер келесі 2 шарт орындалса:1.{a1…ak} сызықтық тәуелсіз 2.  b
b  X b
X b  L (ai…ak) сызықты өрнектейді<X,P> c.k. өлшемі деп к санын атаймыз егер кез-келген элемент сызықтық тауелсіз бола тура осы жүйеге Х жиынына(максимал сызықтық тәуелсіз ішкі жүйенін векторларынын саны) кез келген веторды біріктірсек сызықтық тәуелді жүйе шықса dim x=k.Теорема.(сызықтық кеңістік өлшемі туралы) dim x=n болсын,онда келесі шарттар эквивалентті: 1)X кеңістігінің веторлар жиынының базисі табылады.
L (ai…ak) сызықты өрнектейді<X,P> c.k. өлшемі деп к санын атаймыз егер кез-келген элемент сызықтық тауелсіз бола тура осы жүйеге Х жиынына(максимал сызықтық тәуелсіз ішкі жүйенін векторларынын саны) кез келген веторды біріктірсек сызықтық тәуелді жүйе шықса dim x=k.Теорема.(сызықтық кеңістік өлшемі туралы) dim x=n болсын,онда келесі шарттар эквивалентті: 1)X кеңістігінің веторлар жиынының базисі табылады.
2) X жиынының кез-келген 2 базисінін элементтері саны тең болады.
54.Сызықтық қабықшалар. Ішкі кеңістіктердің қосындысының өлшемі туралы теорема.  сызықтық кеңістігінде кез келген a1,a2,..,ak векторларының жүйесі берілсін.Осы векторлардан құрылған барлық сызықтық өрнектерден тұратын L(a1,a2,..,ak)⇌{⍺1a 1 +⍺2a2+…+⍺kak⃓⍺1,⍺2…,⍺k⋴P} жиынын a1a2,..,ak векторларының сызықтық қабықшасы,ал а1,a2,..,ak векторлардын L(a1,a2,...,ak)сызықтық қабықшасының жасаушылары д.а.Ішкі кеңістіктерінің L=L1+L2+…+Lk қосындысы Ɵ вектор үшін a=a+Ɵ жіктелуінің жалғыз болған жағыдайында және тек сол жағдайында ғана тура қосынды б/ы. Дәләлдеу. Қ.Қандайда бір А⋴L векторы үшін a=a+Ɵ жіктеуі бар болсын:a=a1+a2+…+ak және a=a’1+a’2+…+a’k. Бір жіктеуден екіншісін шегеріп,нөлдік вектор үшін Ɵ=(a1-a’1)+(a2-a’2)+..+(ak-a’k) жіктеуін аламыз.Ɵ вектор үшінa=a+Ɵ жіктеуі жалғыз және Ɵ=Ɵ+Ɵ+..+Ɵ болғандықтан, (a1-a’1)=(a2-a’2)=..=(ak-a’k)= Ɵ демек a1= a’1, a2=a’2,…, ak=a’k болады.
сызықтық кеңістігінде кез келген a1,a2,..,ak векторларының жүйесі берілсін.Осы векторлардан құрылған барлық сызықтық өрнектерден тұратын L(a1,a2,..,ak)⇌{⍺1a 1 +⍺2a2+…+⍺kak⃓⍺1,⍺2…,⍺k⋴P} жиынын a1a2,..,ak векторларының сызықтық қабықшасы,ал а1,a2,..,ak векторлардын L(a1,a2,...,ak)сызықтық қабықшасының жасаушылары д.а.Ішкі кеңістіктерінің L=L1+L2+…+Lk қосындысы Ɵ вектор үшін a=a+Ɵ жіктелуінің жалғыз болған жағыдайында және тек сол жағдайында ғана тура қосынды б/ы. Дәләлдеу. Қ.Қандайда бір А⋴L векторы үшін a=a+Ɵ жіктеуі бар болсын:a=a1+a2+…+ak және a=a’1+a’2+…+a’k. Бір жіктеуден екіншісін шегеріп,нөлдік вектор үшін Ɵ=(a1-a’1)+(a2-a’2)+..+(ak-a’k) жіктеуін аламыз.Ɵ вектор үшінa=a+Ɵ жіктеуі жалғыз және Ɵ=Ɵ+Ɵ+..+Ɵ болғандықтан, (a1-a’1)=(a2-a’2)=..=(ak-a’k)= Ɵ демек a1= a’1, a2=a’2,…, ak=a’k болады.




