Считая концентрацию насыщенного раствора соли равной 1/3, най­ти количество растворенной соли в течение часа, если за это время было влито 180 л воды.

▲ Скорость уменьшения нерастворенного вещества должна быть пропорциональна х и С ₀ – C_t, что приводит к дифференциальному уравнению

где k (предполагается, что k > 0) —коэффициент пропорциональ­ности, подлежащий определению.

В правой части поставлен знак минус, так как каждый из мно dx жителей k, х, С ₀– C_t, через произведение которых выражается , положителен, в то время как < 0, поскольку с течением времени количество нерастворенного вещества должно убывать.

Преобразуя произведение этих множителей и выражая C_t че­рез М, V и х, получаем

Пусть

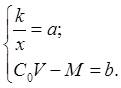(1)

Тогда

и искомое дифференциальное уравнение задачи принимает вид

(2)

Начальное условие:

при t= 0 x=M. (3)

Условие для определения коэффициента а:

при t= 1 ч х=M/2. (4)

Разделяя переменные в уравнении (2) и интегрируя, имеем

(5)

Разложим подынтегральное выражение первого интеграла на простейшие дроби:

Теперь, умножив обе части уравнения (5) на b, можем записать

,

потенцируя, получим

(6)

Полагая в уравнении (6) t =0 и принимая во внимание началь­ное условие (3), находим

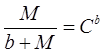(7)

Тогда уравнение (6) примет вид

Решая последнее равенство относительно х, имеем

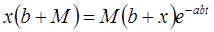
или

откуда общее решение

(8)

Выполним проверку: полагая в уравнении (8) t =0, получим

.

т. е. начальное условие соблюдается.

Дифференцируя уравнение (8) по t, найдем

.

Составим с помощью уравнения (7) выражение

.

Итак,

.

По условию М= 10 кг, V =90 л, С₀=1/3, поэтому по второму из соотношений (1)

Равенство (8) примет вид

.

Согласно условию (4), откуда

Согласно первому из соотношения (1),

k= 0,0255·90=2,295

При V= 180 л

a = 0,0255: 2 = 0,01275; b = (180:3) – 10 = 50; a·b = 0.6375

Искомое количество растворившейся соли

.

Следовательно, количество растворенной соли в течение часаравно М—х= 5,2 кг. ▲

Задача 58. В процессе зарядки коронным разрядом в воздушной или газовой среде происходит процесс ионизации, при котором за 1 сек обра­зуется q положительных и q отрицательных ионов в данном объеме газа. Так как положительные и отрицательные ионы снова соеди­няются между собой, то количество их убывает. Из общего количе­ства п положительных ионов в каждую секунду соединяется часть, пропорциональная квадрату их количества. Коэффициент пропор­циональности k зависит от природы и состояния газа. Найти зави­симость количества ионов п от времени t.

▲ Непосредственно из условия можно записать диф­ференциальное уравнение процесса ионизации

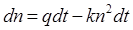(1)

После разделения переменных в уравнении (1) получаем

или

Приведем уравнение к виду

. (2)

Найдем общий интеграл уравнения (2)

откуда после потенцирования имеем

Следовательно, общее решение принимает вид

(3)

С учетом начального условия: при t = 0 п = 0, определим значение произвольной постоянной С.

откуда

С = 1

Подставляя найденное значение постоянной интегрирования в уравнение (3), получаем искомый закон

. ▲

Пример (одн.ур). Для равномерного освещения кусков рудной массы при реализации процесса фотометрической сепарации необходимо определить форму зеркала, чтобы отраженные от него лучи были параллельны оси Ох. Источник света помещен в точке О (Рис.).

Рис.

▲ Рассмотрим кривую сечения поверхности зеркала плоскостью хОу и на этой кривой произвольную точку Р(х,у) (рис.). Угол падения луча равен углу отражения и поэтому OQP = α.

Так как OQP = α, то Δ OPQ — равнобедренный. Таким об­разом,‌ .

Считая у>0, получаем

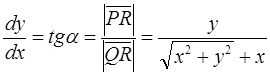
Умножая числитель и знаменатель дроби на выражение , имеем

откуда

или

Проинтегрировав последнее равенство, получаем

или

(1)

По условию кривая должна быть симметричной относительно оси Ох, т. е. уравнение (1) будет выполняться и при у <0. Равен­ство (1) показывает, что искомая кривая есть парабола с осью сим­метрии Ох.

Пусть дано расстояние от источника света О до центра зер­кала S: . Тем самым получаем начальное условие:

при х = -а у = 0 (2)

Подставляя эти значения в уравнение (1), имеем

откуда

С = 2 а.

Значение С =0 не подходит по физическому смыслу задачи. Таким образом, искомая парабола:

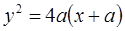
Для этой параболы р = 2 а и, следовательно, фокусное расстоя­ние р/ 2= а, т. е. источник света О находится в фокусе. Плоскость хОу, в которой лежит парабола 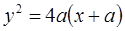, проходит через ось Ох. Уравнение параболы не изменится, если эту плоскость вра­щать вокруг оси Ох. Это значит, что поверхностью зеркала будет служить параболоид вращения. Этот параболоид в сечении с любой плоскостью, проходящей через ось Ох, будет давать параболу, урав­нение которой найдено выше. ▲