Пример. Кусок горной массы массой m сбрасывается вниз по рудоспуску. Найти закон изменения скорости падения v этого куска, если на него действует сила тяжести и тормозящая сила сопротивления воздуха, пропорциональная скорости.
▲ Задача заключается в определении закона изменения скорости v с течением времени t, т.е. v = f(t).
Запишем второй закон Ньютона
где 
- ускорение движущегося куска, F – сила действующая на этот кусок в направлении движения.
Сила F складывается из двух сил: силы тяжести F 1 = mg направленной вниз и силы сопротивления воздуха F 2 = - kv направленной вверх.
Таким образом, уравнение движения куска будет иметь вид
В этом дифференциальном уравнении разделив переменные, получим
(1)
Интегрируя уравнение (1) найдем
(2)
Разрешим (2) относительно v
(3)
Обозначив 
, придем к уравнению
(4)
Если известна начальная скорость падения куска, то можно вычислить значение произвольной постоянной С. Пусть заданы начальные условия: скорость движения куска в начальный момент времени t = 0 равна v 0, тогда
(5)
Подставляя (5) в решение (4) окончательно получим вид искомой функции
. ▲
Пример. Конвейерная лента огибает барабан радиуса r и нагружена силами F 0 и F 1, так, что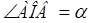 
(рис.). Благодаря трению между барабаном и лентой даже значительно меньшая сила F 0 может уравновешиваться большей силой F 1. Необходимо найти наибольшую силу F 1, которая может уравновешиваться силой F 0, если коэффициент трения равен μ.
▲ Рассмотрим рис.
Рис.
Пример 16. Рассмотрим вентиляцию забоя объемом V(м3), в котором в процессе проведения работ накапливаются вредные газообразные выделения в количестве Z в час. Пусть обмен воздуха в течении 1 часа составляет М (м3/ч), причем приточный воздух содержит вредные вещества в концентрации m на 1 м3. Требуется найти концентрацию Z (на 1 м3) вредных выделений в забое через время t после начала работы, если начальное значение этой концентрации (остаток загрязнений от предыдущей смены) составляет Z0.
▲ За малый промежуток времени dt концентрация вредных выделений Z увеличивается на dZ. Следовательно общее количество выделений составит VdZ и оно будет состоять из выделений, принесенных приточным воздухом - mМdt, и выделений образовавшихся в процессе работы - Zdt за вычетом количества вредных выделений, которое содержалось в извлеченном из забоя за время dt воздухе. Предположим, что за малый промежуток времени dt изменение концентрации вредных выделений равно – ZМdt. Следовательно, уравнение вентиляции забоя имеет вид:
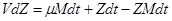или 
Полученное уравнение является линейным неоднородным уравнением, которое будем решать, используя сразу формулу общего решения (1.51):
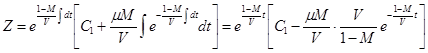или
.
Удовлетворяя начальному условию 
, определим значение произвольной постоянной 
. Таким образом, окончательное решение исходной задачи имеет вид:
.▲
Пример. Определить уравнение кривой, по которой располагается уровень грунтовых вод вблизи скважины, простирающейся до непроницаемого слоя (рис.).
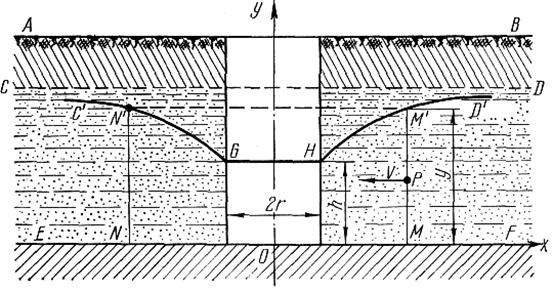
Рис.
▲ Пусть АВ — поверхность земли; CD — поверхность грунтовых вод до устройства колодца; EF — водонепроницаемый слой, ограничивающий снизу поток грунтовых вод.
Если высота воды в скважине поддерживается откачкой на постоянном уровне GH, то поверхность грунтовых вод вблизи от колодца понижается определенным образом.
Линия поверхности грунтовых вод CD переходит в две искривленные ветки C'G и D'H, которые замыкаются на уровне воды GH. Поверхность уровня грунтовых вод представляет собой поверхность вращения вокруг оси Оу меридиональной линии GC' или HD'.
Кривая HD' определяется на основании эмпирического правила, по которому скорость v течения воды в точке Р пропускающего (дренирующего) грунта пропорциональна наклону кривой в точке М', лежащей на вертикали точки Р.
Обозначая коэффициент пропорциональности через k, получим выражение скорости:
.
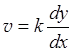
Через боковую поверхность цилиндра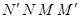 
радиально внутрь протекает количество воды, определяемое дифференциальным уравнением
, (1)
которое для всего цилиндра радиуса х равно расходу воды в скважине.
Разделим переменные в дифференциальном уравнении (1):
,
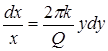Интегрируя, получим
(2)
Постоянную интегрирования находим из условия, что кривая поверхности D'H переходит в поверхность скважины GH.
Если диаметр скважины 2 r, а глубина воды в ней h, то при x=r y=h, т.е.
или
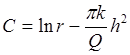(3)
Постоянную интегрирования (3) вводим в уравнение (2) и получаем уравнение искомой кривой
или
. ▲
Пример. Через сосуд емкостью а л, наполненный водным раствором некоторой соли, непрерывно протекает жидкость, причем в единицу времени втекает b л воды и вытекает такое же количество раствора. Найти закон изменения содержания соли в сосуде в зависимости от времени протекания жидкости через сосуд.
▲ В данный момент времени t в сосуде содержится х кг соли, следовательно, в каждом литре раствора содержится x/a кг соли, а в b литрах bx/a кг.
Если бы в течение единицы времени, начиная с момента t, концентрация раствора оставалась неизменной, какой она была в момент t, то количество соли в сосуде за эту единицу времени уменьшилось бы на bx/a кг; такова скорость уменьшения количества соли сосуде для момента t.
С другой стороны, производная
равна скорости прироста количества соли в момент t, поэтому скорость уменьшения количества соли в момент t равна — 
.
Итак,
Разделяя переменные, получим
откуда
Потенцируя, найдем
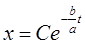(1)
где C — произвольная постоянная.
Предположим, что в некоторый начальный момент t= 0количество соли в сосуде равно A кг.
Полагая в равенстве (1) t = 0, найдем
C = A.
Искомый закон изменения содержания соли
.▲
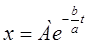РАСТВОРЕНИЕ ТВЕРДЫХ ТЕЛ
Пусть при постоянной температуре скорость растворения твердого тела в жидкости пропорциональна количеству этого вещества, еще могущего раствориться до полного насыщения жидкости.
Пусть Р — количество вещества, дающее насыщенный раствор; х — количество растворившегося вещества.
Тогда дифференциальное уравнение процесса
где k — эмпирический коэффициент пропорциональности, t — время. Разделяя переменные и интегрируя, находим
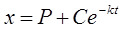(1)
Начальное условие: при t = 0 х = 0, откуда
и постоянная интегрирования
C = -P (2)
Подставляем выражение (2) в общее решение (1) и получаем закон зависимости количества растворившегося вещества от времени:
 |
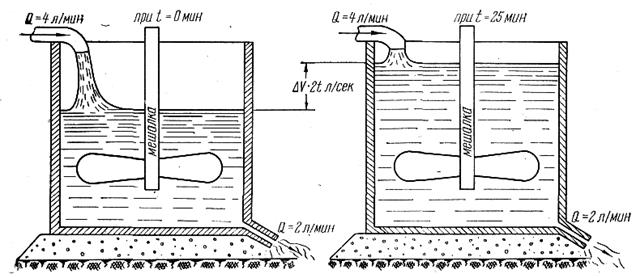Задача 54. Резервуар наполнен 75 л суспензии, содержащего 3 кг растворенного реагента. Приток воды составляет 4 л в минуту, а расход смеси из сосуда 2 л в минуту. Концентрация поддерживается равномерной посредством перемешивания (рис.). Найти количество реагента, которое будет содержаться в резервуаре через 25 мин.
Рис.
▲ Пусть х — количество реагента в резервуаре в момент t, кг; t — время, отсчитываемое от начального момента t0, мин; —dx — количество реагента, выходящее из резервуара за время dt (знак минус обусловлен тем, что х — убывающая функция времени), кг.
К моменту t в резервуар поступило 4 t л воды и вышло 2 t л суспензии. Увеличение суспензии составляет 2 t л.
Таким образом, общее количество жидкости достигло 75+2 t л и в ней растворилось х кг реагента.
За время dt уходит – dx кг реагента и 2 dt л суспензии.
Считая концентрацию суспензии постоянной, получим количество реагента в одном литре 
кг. Следовательно, за короткий промежуток времени dt количество реагента уменьшится на 
кг.
Итак, элементарное уравнение движения жидкости будет иметь вид
Разделяя переменные в этом уравнении, имеем:
.
Интегрируя это уравнение, с учетом того, что в начальный момент времени t 0 = 0 в резервуаре было 3 кг реагента (х 0 = 3 кг), а через 25 мин, т.е. в момент времени t 1= 25 сек, его стало х 1 = х кг, получим
или
Потенцируя полученное выражение, получаем
,
или искомое количество реагента в резервуаре будет равно
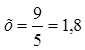кг. ▲
Пример. Подвергая 10 кг соли действию 90 л воды, обнаружили, что в течение часа растворилась половина этого количества.
