(9)
Характеристическое уравнение
имеет корни 
, следовательно, в силу теоремы 2 точка покоя систем (8) и (9) неустойчива (т.к. 
).
Пример 2.
Исследовать на устойчивость точку покоя 
системы
(10)
Имеем:
(10a)
т.е. 
удовлетворяют условиям теорем 1 и 2. Характеристическое уравнение для системы первого приближения
(11)
т.е. 
имеет корни 
с отрицательными действительными частями. Поэтому точки покоя систем (10) и(11) асимптотически устойчивы.
Пример 3.
Исследовать на устойчивость точку покоя системы
(12)
Характеристическое уравнение системы I приближения 
имеет чисто мнимые корни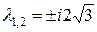 
критический случай. Исследование по I приближению невозможно. В данном случае легко подбирается функция Ляпунова
1) 
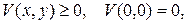
2) 
причем вне некоторой окрестности начала координат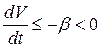 
, следовательно, точка покоя по теореме Ляпунова асимптотически устойчива.
Система уравнений первого приближения
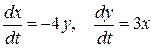(13)
имела в точке покоя центр. Наличие нелинейных членов в системе (12) превратило этот центр в устойчивый фокус.
Рассмотрим ситуацию последнего примера в общем виде. Пусть система I приближения для системы
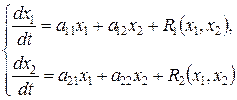(14)
имеет точку типа центра в начале координат. Предположим, что нелинейные члены 
имеют порядок выше первого относительно 
. Эти нелинейные члены в достаточно малой окрестности начала координат малы по сравнению с линейными членами, но всё же они несколько искажают поле направлений, определяемое линейной системой первого приближения, поэтому выходящая из некоторой точки 
траектория после обхода начала координат, вообще говоря, не попадет в точку траектория не замыкается.
Если после такого обхода начала координат все траектории приближаются к нему, то в начале координат возникает устойчивый фокус, если же траектории удаляются от начала координат, то возникает неустойчивый фокус.
В виде исключения возможен также случай, когда все траектории нелинейной системы, расположенные в окрестности начала координат, остаются замкнутыми, однако наиболее типична ситуация, при которой лишь некоторые (может быть и ни одной)
замкнутые кривые останутся замкнутыми, а остальные превращаются в спирали. Такие замкнутые траектории, в окрестности которых все траектории являются спиралями, называются предельными циклами.
Рис. 1 Рис. 2
Если близкие к предельному циклу траектории являются спиралями, приближающиеся при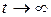 
к предельному циклу, то предельный цикл называется устойчивым (аттрактором); если близкие к предельному циклу траектории являются спиралями, удаляющимися от предельного цикла при 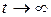, то предельный цикл называется неустойчивым (репеллером); если же с одной стороны предельного цикла при 
спирали приближающиеся к предельному циклу, а с другой стороны удаляются от него (рис. 2), то предельный цикл называется полуустойчивым.
Итак, переход от системы I приближения (5) к системе (14) приводит, вообще говоря, к превращению центра в фокус, окруженный 
(может быть и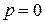 
) предельными циклами.
В приложениях устойчивым предельным циклам обычно соответствуют автоколебательные процессы, т.е. периодические процессы, в которых малые возмущения практически не изменяют амплитуды и частоты колебаний.
4. Дифференциальные уравнения с частными производными первого порядка
Наиболее общее уравнение с частными производными I порядка с 
независимыми переменными может быть записано в виде
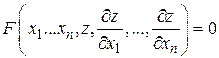, (1)
где 
– заданная функция, 
- искомая функция,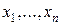 
– независимые переменные.
Пример 1.
.
Интегрируя, имеем
,
где 
- произвольная функция от 
.
Пример 2.
.
Интегрируя по 
, получим
,
где - произвольная функция . Интегрируем теперь по :
,
где 
- произвольная функция от . Окончательно имеем:
,
где
-
произвольная функция.
Из приведенных примеров видно, что общее решение дифференциального уравнения с частными производными I порядка зависит от одной произвольной функции, общее решение уравнения II порядка – от двух произвольных функций.
Линейным неоднородным уравнением или квазилинейным уравнением I порядка в частных производных называется уравнение вида:
. (2)
Это уравнение линейно относительно производных, но может быть нелинейным относительно неизвестной функции 
.
Если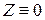 
, а коэффициенты 
не зависят от , то уравнение (2) называется линейным однородным.
Рассмотрим вначале квазилинейное уравнение с двумя независимыми переменными
, (3)
где 
непрерывны в некоторой области изменения переменных и не обращаются в нуль одновременно.
Рассмотрим непрерывное векторное поле
.
Векторные линии этого поля (т.е. линии, касательные к которым в каждой точке имеют направление, совпадающее с направлением вектора 
в той же точке) определяются из условия коллинеарности вектора 
, направленного по касательной к искомым линиям, и вектора поля :
. (4)
Это система дифференциальных уравнений векторных линий.
Поверхности, составленные из векторных линий, точнее, поверхности целиком содержащие векторные линии, имеющие хотя бы одну общую точку с поверхностью, называются векторными поверхностями.
Очевидно, векторные поверхности можно получить, рассматривая множество точек, лежащих на произвольно выбранном непрерывно зависящем от параметра однопараметрическом семействе векторных линий. Векторная поверхность характеризуется тем, что вектор 
, направленный по нормали к поверхности в любой ее точке, ортогонален вектору поля :
(5)
Если векторная поверхность задана уравнением 
, то вектор
,
и условие (5) принимает вид:
. (3)
Если же векторная поверхность задана уравнением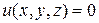 
(неявно), т.е.
,
то условие (5) имеет следующий вид:
. (6)
Следовательно, для нахождения векторных поверхностей надо проинтегрировать квазилинейное уравнение (3) или линейное однородное уравнение (6) в зависимости от того, ищем ли мы уравнение искомых векторных поверхностей в явном или неявном виде.
Т.к. векторные поверхности могут быть составлены из векторных линий, то интегрирование уравнений (3) или (6) сводится к интегрированию системы обыкновенных дифференциальных уравнений векторных линий (4).
4.1. Первые интегралы систем дифференциальных уравнений
Рассмотрим систему дифференциальных уравнений
. (7)
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием системы (7), но уже легко интегрирующееся, например, являющееся уравнением вида
)
или уравнением, которое может быть сведено путем замены переменных к какому-нибудь интегрируемому типу уравнений с одной неизвестной функцией.
Пример 3.
.
Складывая обе части равенств, найдем интегрируемую комбинацию
,
т.е.
,
откуда
.
Вычитая, найдем вторую интегрируемую комбинацию
,
откуда
.
Итак,
, 
.
Следовательно,
.
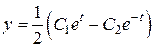Одна интегрируемая комбинация дает возможность получить одно соотношение
,
связывающее неизвестные функции и независимую переменную; такое соотношение называется первым интегралом системы (7).
Итак, первым интегралом
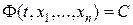(8)
системы уравнений (7) называется соотношение, не равное тождественно постоянной, содержащее в левой части независимую переменную и искомые функции и принимающее постоянное значение, если вместо искомых функций подставить какое-нибудь решение системы (7).
Геометрически первый интеграл (8) при фиксированном 
можно интерпретировать как - мерную поверхность в 
-мерном пространстве с координатами 
, обладающую тем свойством, что каждая интегральная кривая, имеющая общую точку с этой поверхностью, целиком лежит на поверхности.
При переменном получаем семейство непересекающихся поверхностей, состоящих из точек некоторого 
- параметрического семейства интегральных кривых системы (7).
Если найдено 
интегрируемых комбинаций, то получаем первых интегралов
(9)
Если все эти интегралы независимы, то есть если хотя бы один из определителей
,
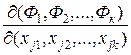где 
какие-нибудь функций из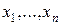 
, не равен нулю, то из системы (9) можно выразить неизвестных функций через остальные и, подставив в систему (7), понизить ее размер. Если 
и все интегралы независимы, то все неизвестные функции определяются из (9).
Пример 4.
где 
. Умножив первое уравнение на , второе – на 
, третье – на 
и складывая, получим
,
т.е. имеем I- й интеграл:
.
Умножим первое уравнение на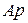 
, второе – на 
, третье – на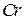 
и складывая, имеем
.
Откуда получаем следующий I- й интеграл:
.
За исключением случая 
, когда система интегрируется непосредственно, найденные первые интегралы независимы и, следовательно, можно исключить две неизвестные функции, а для нахождения третьей получим одно уравнение с разделяющимися переменными.
Для нахождения интегрируемых комбинаций часто удобно переходить к так называемой симметричной форме записи системы уравнений (7):
, (10)
где
= 
.
Характеристики
Вернемся к системе дифференциальных уравнений векторных линий
. (11)
Пусть 
, 
- два независимых первых интеграла системы (10). Выделим из двухпараметрического семейства векторных линий
, ,
называемых характеристиками уравнения (3) (или (6)), произвольным способом однопараметрическое семейство, устанавливая какую-нибудь (произвольную) непрерывную зависимость 
между параметрами 
и 
. Исключая из системы
, ,
параметры и , получим искомое уравнение векторных поверхностей
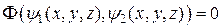, (12)
где 
– произвольная функция. Тем самым найден общий интеграл квазилинейного уравнения (3), зависящий от произвольной функции.
Если требуется найти не произвольную векторную поверхность поля
,
а поверхность, проходящую через заданную линию, определяемую уравнениями 
, то функция в (12) будет уже не произвольной, а определится путем исключения переменных 
из системы уравнений
, 
,
которые должны одновременно удовлетворяться в точках заданной линии 
, через которую мы проводим характеристики, определяемые уравнениями .
Задача станет неопределенной, если заданная линия является характеристикой, т.к. в этом случае эту линию можно включить в различные однопараметрические семейства характеристик и тем самым получить различные интегральные поверхности, проходящие через эту линию.
Таким образом, характеристики – это кривые, через которые проходит бесконечное множество интегральных поверхностей.
Итак, общий интеграл квазилинейного уравнения
, (3)
зависящий от произвольной функции может быть получен следующим образом: интегрируем вспомогательную эквивалентную систему обыкновенных дифференциальных уравнений
(4)
и, найдя два независимых первых интеграла этой системы
, ,
получаем искомый интеграл в виде 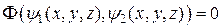, где – произвольная функция.
Уравнение интегральной поверхности уравнения (3), проходящей через заданную линию , можно найти, если взять функцию не произвольно, а определив функцию 
путем исключения из уравнений
, ,
в результате чего получим уравнение , и искомым интегралом будет .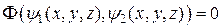
Пример 5.
Найти общий интеграл уравнения
.
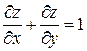Вспомогательная система уравнений имеет вид (здесь 
)
.
Ее первые интегралы: 
. Общий интеграл: 
, где – произвольная функция.
Пример 6.
Найти интегральную поверхность уравнения
,
проходящую через кривую 
.
Интегрируем систему
,
откуда имеем первые интегралы: 
. Исключаем из уравнений
, 
.
Получаем 
, откуда 
.
Пример 7.
Найти интегральную поверхность того же уравнения, проходящую через окружность
.
Заданная кривая является одной из векторных линий (характеристик), таким образом, задача неопределенна. Действительно, интегральными поверхностями рассматриваемого уравнения являются всевозможные поверхности вращения 
, ось которых совпадает с осью 
. Существует бесконечное множество таких поверхностей, проходящих через заданную окружность, например, параболоиды вращения 
, 
, 
,, сфера 
и т.д.
5. Линейные однородные дифференциальные уравнения в частных производных первого порядка с независимыми переменными.
Рассмотрим уравнение вида
, (1)
где 
– заданные функции, непрерывные и дифференцируемые в рассматриваемой области изменения независимых переменных 
; – искомая функция. Наряду с уравнением (1) запишем систему обыкновенных дифференциальных уравнений
, (2)
