5. Затраты времени на сборку прибора у 70 сборщиков цеха имеют следующее распределение:
| Время, мин | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Число сборщиков |
Вычислить выборочные характеристики этого распределения: среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. Для испытания шерстяной ткани на прочность произведены две выборки объемом в 10 и 12 образцов. Средняя прочность оказалась равной 135 и 136 г при исправленных выборочных дисперсиях 4 и 6. Считая выборки извлеченными из нормальных совокупностей, определить при уровне значимости 0,01 существенность расхождения между средними в обеих выборках.
7. В результате исследования зависимости выпуска валовой продукции (Y,тыс.руб.) от основных фондов (Х, тыс.руб.) однотипных предприятий получены следующие данные:
| Х | ||||||
| Y |
Полагая, что между Х и Y имеет место линейная зависимость, определить выборочный коэффициент корреляции, объяснить его смысл, проверить значимость коэффициента корреляции при уровне значимости 0,05. Построить уравнение регрессии и объяснить его.
Вариант № 9
(Первая буква фамилии студента: З, И)
1. Для производственной практики на 30 студентов предоставлено 10 мест в Саратове, 8 в Казани, остальные в Самаре. Какова вероятность того, что три определенных студента попадут на практику в один город?
2. Вероятность бесперебойной работы в течение часа первого станка равна 0,8; второго - 0,85; третьего - 0,9. Какова вероятность того, что в течение часа произойдет нарушение в работе: а) только одного станка; б) всех станков?
3. На сборку поступают детали с трех автоматов. Первый дает в среднем 98% годных деталей, второй - 99%, а третий - 97%. Найти вероятность попадания на сборку бракованной детали, если она выбрана случайным образом, а производительность автоматов одинакова.
4. Диаметр подшипников, выпускаемых заводом, представляет случайную величину, распределенную по нормальному закону с математическим ожиданием 16 мм и дисперсией 0,16 мм2. Найти вероятность брака при условии, что для диаметра подшипника разрешается допуск (±0,7) мм.
5. В результате выборочного обследования получено распределение времени на выполнение технологической операции (Х, с) 20 рабочими:
| хi | |||||
| Число рабочих |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. На заводе имеются центробежные насосы, закупленные на предприятиях А и В по 10 шт. Насосы, закупленные на предприятии А, проработали до поломки в среднем 100 дней, исправленное среднее квадратическое отклонение 10 дней; насосы, закупленные на предприятии В, проработали до поломки в среднем 105 дней, исправленное среднее квадратическое отклонение 9 дней. Заводу требуется приобрести еще насосы. Специалист по материально-техническому снабжению решил, что надо закупать насосы на предприятии В. Считая, что выборки извлечены из нормально распределенных генеральных совокупностей, проверить, действительно ли насосы, выпущенные предприятием В, лучше (a =0,01).
7. Экономическое обследование пяти предприятий дало следующие результаты:
| Х | ||||||
| Y | , |
где Y -выпуск готовой продукции на одного работающего, тыс. руб.;
Х -энерговооруженность труда работающего, кВт×ч.
Полагая, что между Х и Y имеет место линейная зависимость, определить выборочный коэффициент корреляции, объяснить его смысл, проверить значимость коэффициента корреляции при уровне значимости 0,05. Построить уравнение регрессии и объяснить его.
Вариант № 10
(Первая буква фамилии студента: Д, Е, Ж)
1. Из десяти билетов выигрышными являются 3 билета. Найти вероятность того, что среди взятых наудачу четырех билетов: а) выигрышным будет только один; б) выигрышных и невыигрышных билетов будет поровну.
2. Известно, что первый станок простаивает 5%, второй - 10%, а третий - 15% рабочего времени. Какова вероятность того, что в случайно выбранный момент окажутся работающими: а) один станок; б) два станка; в) хотя бы два станка?
3. Первый заготовительный цех изготовил 1000 деталей, второй в 2 раза больше, а третий столько, сколько первые два, вместе взятые. При этом продукция первого цеха содержит 0,3% брака, второго - 0,2% и третьего - 0,4% брака. Все детали общей партией поступают на сборку. Наудачу берут одну деталь. Найти вероятность того, что она годная.
4. На автомате изготовляются заклепки. Диаметр их головок представляет собой случайную величину, распределенную по нормальному закону, имеет среднее значение, равное 2 мм, и дисперсию, равную 0,01 мм2. Найти вероятность того, что диаметр головки заклепки будет от 2,1 до 2,3 мм. Какие размеры диаметра головки заклепки можно гарантировать с вероятностью 0,95?
5. Имеются данные о производительности труда 50 рабочих:
| Произведено продукции одним рабочим за смену, шт. | |||||
| Число рабочих |
Определить среднюю производительность труда одного рабочего, а также характеристики вариации. Дать экономическую интерпретацию полученных результатов.
6. С целью увеличения срока службы разработана новая конструкция пресс-формы. Старая пресс-форма в 10 испытаниях прослужила в среднем 4,4 месяца с исправленным средним квадратическим отклонением 0,05 месяца. Предлагаемая новая пресс-форма при 6 испытаниях требовала замены в среднем после 5,5 месяца с исправленным средним квадратическим отклонением 0,09 месяца. Считая, что выборки извлечены из нормально распределенных генеральных совокупностей, проверить, действительно ли новая конструкция лучше (используйте a =0,01).
7. По данным таблицы изменения веса поросят (Y, кг) в зависимости от их возраста (Х, недели) построить эмпирическую линию регрессии и по ее виду определить предполагаемую форму связи Y и Х. Оценить тесноту корреляционной связи (уровень значимости принять равным 0,05). Построить уравнение регрессии, объяснить его.
| Х | |||||||||
| Y | 1,3 | 2,5 | 3,9 | 5,2 | 6,3 | 7,5 | 9,0 | 10,8 | 13,1 |
Вариант № 11
(Первая буква фамилии студента: В, Г)
1. Имеются изделия трех сортов. Число изделий каждого сорта равно, соответственно, 4, 3, 5. Для контроля наудачу берут 6 изделий. Определить вероятность того, что среди них одно изделие I сорта, два - II сорта, три - III сорта.
2. В цехе три участка. Вероятность невыполнения плана первым участком составляет 0,02, для второго и третьего участков эти вероятности, соответственно, равны 0,05 и 0,01. Найти вероятность того, что к моменту подведения итогов плановое задание будет выполнено: а) олько одним участком; б) двумя участками; в) хотя бы одним участком.
3. Литье в болванках поступает из трех заготовительных цехов: 60 штук из первого цеха, а из второго и третьего, соответственно, в 2 и 4 раза больше, чем из первого. При этом материал первого цеха имеет 1% брака, второго - 2%, а третьего - 2,5%. Найти вероятность того, что наудачу взятая болванка окажется без дефектов.
4. Длина изготовляемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону. Средняя длина детали равна 15 см, среднее квадратическое отклонение равно 0,2 см. Найти вероятность брака, если допустимые размеры детали должны быть (15±0,3) см. Какую точность длины изготавливаемой детали можно гарантировать с вероятностью 0,97?
5. В результате выборочного обследования получены данные о составе строительных бригад:
| Число рабочих в бригаде, чел. | 16-20 | 21-25 | 26-30 | 31-35 | 36-40 | 41-45 | 46-50 |
| Число бригад |
Определить среднее число рабочих в бригаде, коэффициент вариации.
6. По выборочным данным 15 предприятий одной отрасли найдена средняя себестоимость единицы продукции. Она составила 
в=4,85 руб. При этом исправленное среднее квадратическое отклонение S xоказалось равным 0,94 руб. Аналогично была вычислена средняя себестоимость единицы продукции по 12 предприятиям той же отрасли, она составила 
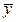в=5,07 руб., а S y=1,02 руб. При уровне значимости 0,01 выявить существенность различия средней себестоимости единицы продукции на предприятиях, считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y.
7. Определить тесноту связи выпуска продукции Х (тыс.шт.) и себестоимость одного изделия Y (руб.) на основе следующих данных:
| X | |||||
| Y | 1,9 | 1,7 | 1,8 | 1,6 | 1,4 |
Проверить значимость выборочного коэффициента корреляции при уровне значимости 0,05. Построить линейное уравнение регрессии и объяснить его.
Вариант № 12
(Первая буква фамилии студента: А, Б)
1. 17 студентов группы, среди которых 8 девушек, разыгрывают 7 билетов. Какова вероятность того, что среди обладателей билетов окажутся: а) только 4 девушки; б) хотя бы одна девушка?
2. Три баскетболиста производят по одному броску мяча. Вероятности попадания в корзину первым, вторым, третьим баскетболистом равны, соответственно, 0,9; 0,8; 0,7. Найти вероятность того, что произведет удачно бросок: а) только один баскетболист; б) хотя бы один баскетболист.
3. В одной студенческой группе обучаются 24 студента, во второй - 36 студентов, в третьей - 40 студентов. По теории вероятностей получили отличные оценки 6 студентов первой группы, 6 студентов второй группы, и 4 студента третьей группы. Наудачу выбранный студент оказался получившим по теории вероятностей оценку "отлично". Какова вероятность того, что он учится во второй группе?
4. Детали, изготовленные автоматом, по размеру диаметра распределяются по нормальному закону. Известно, что математическое ожидание равно 4,8 см, а дисперсия равна 0,81 см2. Найти: а) вероятность того, что диаметр наудачу взятой детали будет в пределах от 5,7 до 7,5 см; б) границы, в которых следует ожидать размер диаметра детали, если вероятность невыхода за эти границы равна 0,9545.
5. Дано распределение расхода сырья, идущего на изготовление одного изделия (Х,г):
| хi | |||||
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. Для изучения норм выработки двух бригад завода,выполняющих одинаковый вид работ, проведено выборочное обследование затрат времени на изготовление одной детали. Для первой бригады (7 чел.) среднее время в=25 мин, исправленная выборочная дисперсия 
=2,5; для второй бригады (8 чел.), соответственно,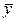 
в=30 мин,
=3. Считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y, проверить при уровне значимости 0,05, одинаковы ли для этих бригад средние затраты времени на выполнение одной детали.
7. По пяти предприятиям одной отрасли имеются данные о валовой продукции и издержкам производства:
| Валовая продукция, тыс. шт. | |||||
| Издержки производства, тыс. руб. | 4,5 | 3,5 |
Проверить значимость коэффициента корреляции при a =0,05. Если коэффициент корреляции значим, то написать уравнение регрессии, объяснить его смысл. Спрогнозировать издержки производства при заданном объеме валовой продукции в 65 тыс.шт.
 |
ПРИМЕРНЫЕ Вопросы
ДЛЯ ПОДГОТОВКИ к экзамену (ЗАЧЕТУ)
1. Основные понятия и определения теории вероятностей. Виды случайных событий. Классическое и статистическое определение вероятности события. Свойства вероятностей события. Непосредственный подсчет вероятностей. Основные формулы комбинаторики.
2. Сложные события. Сумма и произведение событий. Теорема сложения вероятностей для несовместных событий и следствия из нее. Теорема сложения вероятностей для совместных событий.
3. Зависимые и независимые события. Условная вероятность события. Теорема умножения вероятностей для конечного числа зависимых событий. Теорема умножения вероятностей для конечного числа независимых событий.
4. Формула полной вероятности. Формула Байеса.
5. Повторные независимые испытания. Формула Бернулли. Наивероятнейшая частота.
6. Повторные независимые испытания. Локальная теорема Муавра-Лапласа. Теорема Пуассона.
7. Случайная величина. Виды случайных величин. Закон распределения случайной величины и способы его задания (табличный, графический, аналитический).
8. Интегральная функция распределения случайной величины, ее свойства.
9. Дифференциальная функция распределения случайной величины (плотность распределения вероятности), ее свойства. Выражение интегральной функции через дифференциальную функцию распределения случайной величины.
10. Характеристики случайной величины: математическое ожидание. Свойства математического ожидания.
11. Характеристики случайной величины: дисперсия и среднее квадратическое отклонение. Свойства дисперсии.
12. Биномиальный закон распределения случайной величины, его свойства, характеристики случайной величины, полигон распределения.
13. Распределение Пуассона, его свойства, характеристики случайной величины, полигон распределения.
14. Равномерное распределение случайной величины: дифференциальная и интегральная функции распределения, их графики; характеристики распределения; вероятность попадания случайной величины в заданный интервал.
15. Показательное распределение случайной величины: дифференциальная и интегральная функции распределения, их графики, характеристики распределения, вероятность попадания случайной величины в заданный интервал. Характеристическое свойство показательного распределения.
16. Нормальный закон распределения случайной величины. Дифференциальная функция распределения, ее свойства. Нормированное нормальное распределение. Кривая Гаусса. Влияние параметров распределения на форму и положение нормальной кривой.
17. Теоретико-вероятностный смысл параметров нормального распределения (вывод формул математического ожидания и дисперсии).
18. Интеграл вероятностей (функция Лапласа). Свойства функции Лапласа. Выражение интегральной функции нормального распределения через функцию Лапласа.
19. Вероятность попадания в заданный интервал нормально распределенной случайной величины. Вероятность заданного отклонения значений случайной величины от ее математического ожидания. Правило трех “сигм”.
20. Распределение Пирсона (χ 2 - распределение). Распределение Стьюдента (t - распределение).
21. Распределение Стьюдента (t - распределение). Распределение Фишера - Снедекора (F - распределение).
22. Понятие закона больших чисел. Неравенство Чебышева.
23. Теорема Чебышева, частный случай теоремы. Теорема Бернулли. Понятие о теореме Ляпунова. Частный случай теоремы Ляпунова.
24. Статистическая совокупность (генеральная и выборочная). Ряды распределения (дискретные и интервальные). Графическое изображение рядов распределения.
25. Статистическая совокупность (генеральная и выборочная). Ряды распределения. Накопленные частоты и частости. Эмпирическая функция распределения.
26. Выборочные средние статистических распределений: средняя, мода, медиана.
27. Выборочные характеристики рассеяния статистических распределений: дисперсия, среднее квадратическое отклонение, коэффициент вариации.
28. Статистические оценки параметров распределения. Точечные оценки. Свойства статистических оценок параметров распределения (несмещенность, состоятельность, эффективность). Оценка генеральной средней по выборке.
29. Статистические оценки параметров распределения. Точечные оценки. Свойства статистических оценок параметров распределения (несмещенность, состоятельность, эффективность). Оценка генеральной дисперсии и среднего квадратического отклонения по выборке. Исправленная выборочная дисперсия.
30. Интервальные оценки параметров распределения. Точность оценки. Доверительный интервал и доверительная вероятность. Доверительные интервалы для оценки математического ожидания нормально распределенной случайной величины при известном среднем квадратическом отклонении.
31. Интервальные оценки параметров распределения. Точность оценки. Доверительный интервал и доверительная вероятность. Доверительные интервалы для оценки математического ожидания нормально распределенной случайной величины при неизвестном среднем квадратическом отклонении.
32. Статистические гипотезы. Ошибки 1-го и 2-го рода. Статистический критерий. Наблюдаемое значение критерия. Критическая область. Область принятия гипотезы. Критические точки. Уровень значимости. Отыскание критической области.
33. Проверка гипотезы о нормальном законе распределения генеральной совокупности.
34. Сравнение дисперсий двух нормально распределенных генеральных совокупностей.
35. Сравнение средних двух нормально распределенных генеральных совокупностей при неизвестных дисперсиях.
36. Сравнение средних двух нормально распределенных генеральных совокупностей при известных дисперсиях.
37. Сравнение вероятностей.
38. Функциональная и статистическая зависимости. Условные распределения. Условные средние.
39. Корреляционная зависимость. Виды корреляционной зависимости. Уравнение регрессии. Понятие о методе наименьших квадратов.
40. Линейная корреляционная зависимость. Оценивание параметров выборочного уравнения линейной регрессии методом наименьших квадратов. Коэффициент регрессии, его экономический смысл.
41. Выборочный линейный коэффициент корреляции, его свойства.
42. Выборочный линейный коэффициент корреляции, проверка его значимости. Коэффициент детерминации.
43. Простейшие случаи нелинейной корреляционной зависимости: параболическая. Отыскание параметров уравнения регрессии методом наименьших квадратов.
44. Простейшие случаи нелинейной корреляционной зависимости: гиперболическая. Отыскание параметров уравнения регрессии методом наименьших квадратов.
45. Выборочное корреляционное отношение, его свойства.
Рекомендуемая литература
Основная литература
1. Репин, О.А. Математика для экономистов. Теория вероятностей и математическая статистика / О.А. Репин, Е.И. Суханова, Л.К. Ширяева. - Самара: Изд-во Самар. гос. экон. акад, 2005.
2. Репин, О.А. Математика для экономистов. Сборник задач по теории вероятностей и математической статистике: учеб.пособие / О.А. Репин, Е.И. Суханова, Л.К. Ширяева. - Самара: Изд-во Самар. гос. экон. акад., 2005.
Дополнительная литература
3. Айвазян, С.А. Теория вероятностей и прикладная статистика / С.А. Айвазян, В.С. Мхитарян. - М.: ЮНИТИ-ДАНА, 2001.
4. Вентцель, Е.С. Задачи и упражнения по теории вероятностей /Е.С. Вентцель, Л.А. Овчаров. - М.: Высш. школа, 2002.
5. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высш. школа, 2003.
6. Гмурман, В.Е. Теория вероятностей и математическая статистика. - М.: Высш. школа, 2003.
7. Колемаев, В.А. Теория вероятностей и математическая статистика / В.А. Колемаев, В.Н. Калинина. - М.: ЮНИТИ-ДАНА, 2003.
8. Кремер, Н.Ш. Теория вероятностей и математическая статистика: учеб.для вузов. - М.: ЮНИТИ-ДАНА, 2007.
9. 2. Репин, О.А. Сборник задач по теории вероятностей и математической статистике: учеб.пособие / О.А. Репин, Е.И. Суханова, Л.К. Ширяева. –М.: Вега-Инфо, 2009.
ПРИЛОЖЕНИЯ
Приложение 1
Таблица значений функции f (х) = 
| х | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | ||||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | ||||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | ||||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Приложение 2
