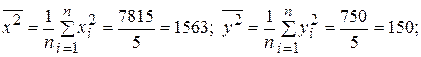
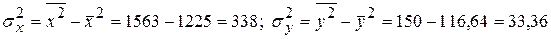.
Таким образом,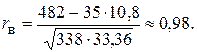 
Проверим значимость выборочного коэффициента корреляции. Для этого выдвигаем гипотезы:
Н 0: r ген=0, Н 1: r ген¹ 0.
Уровень значимости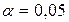 
.
Для проверки нулевой гипотезы используем случайную величину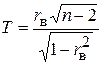 
, имеющую распределение Стьюдента с k = n -2=3 степенями свободы. По выборочным данным найдем наблюдаемое значение критерия Т набл= 
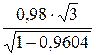»8,53. По таблице критических точек распределения Стьюдента определим t крит.дв(0,05;3)=3,18. Сравниваем Т набл и t крит(0,05;3). Так как ½ Т набл½> t крит.дв(0,05;3), то есть Т набл попало в критическую область, нулевая гипотеза отвергается, справедлива конкурирующая гипотеза: r ген¹0. Признаки Х и Y коррелированны, r в значим. Так как ½ r в½ близок к единице, следовательно, выпуск валовой продукции и основные фонды находятся в тесной корреляционной зависимости.
Найдем коэффициент детерминации. D = r в2×100%=95,8%, то есть вариация выпуска валовой продукции в среднем на 95,8% объясняется вариацией основных фондов.
Выразим эту связь аналитически в виде линейного уравнения регрессии:
- 
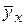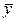» a 1(х - 
),
;
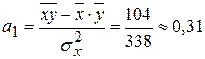или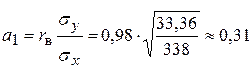 
.
Таким образом, 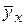-10,8»0,31 (x -35) или 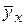»0,31 x -0,05.
Из уравнения следует, что с увеличением основных фондов на 1 тыс.руб. выпуск валовой продукции увеличится в среднем на 0,31 тыс. руб.
Найдем по уравнению регрессии выпуск валовой продукции, если основные фонды составят 80 тыс.руб.:
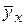»0,31 × 80- 0,05=24,75 (тыс. руб.)
варианты Контрольной работы
Вариант № 1
(Первая буква фамилии студента: Щ, Э, Ю, Я)
1. В партии готовой продукции, состоящей из 25 деталей, 5 бракованных. Определить вероятность того, что при случайном выборе четырех деталей: а) все окажутся небракованными; б) бракованных и небракованных изделий будет поровну.
2. В городе три коммерческих банка, оценка надежности которых 0,95; 0,90 и 0,85, соответственно. В связи с определением хозяйственных перспектив развития города администрацию интересует ответ на вопрос: какова вероятность того, что в течение года: а) обанкротятся все три банка; б) обанкротится хотя бы один банк.
3. В ящике находятся изделия, сделанные на трех станках: 20 - на первом станке, 18 - на втором и 14 - на третьем. Вероятности того, что изделия, изготовленные на первом, втором и третьем станках, отличного качества, соответственно, равны 0,7; 0,85; 0,9. Взятое наудачу изделие оказалось отличного качества. Какова вероятность того, что оно изготовлено на втором станке?
4. Диаметр деталей, изготовленных автоматом, представляет собой случайную величину, распределенную по нормальному закону. Дисперсия ее равна 4 мм2, а математическое ожидание - 20,5 мм. Найти вероятность брака, если допустимые размеры диаметра должны быть (20±3) мм.
5. Группа рабочих изготавливает одинаковую продукцию. Дан ряд распределения рабочих по числу изготавливаемых за смену деталей:
| Число деталей | |||||
| Число рабочих |
Вычислить выборочные среднюю, размах вариации, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. В результате специального обследования получено выборочное распределение стажа работников завода (Х - стаж работы, лет; 
- эмпирические частоты; 
- теоретические частоты нормального распределения):
| x i | |||||||||
|
| |||||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака Х генеральной совокупности с эмпирическим распределением выборки.
7. Средняя урожайность пшеницы и глубина вспашки по фермерским хозяйствам даны в следующей таблице:
| Глубина вспашки, см | ||||||
| Средняя урожайность, ц\га | 8,1 | 8,3 | 8,2 | 9,1 | 10,3 | 10,8 |
При a =0,05 проверить значимость корреляционной связи глубины вспашки и средней урожайности пшеницы. Если связь значима, составить уравнение регрессии. Объяснить его. Спрогнозировать урожайность пшеницы при глубине вспашки в 11,5 см.
Вариант № 2
(Первая буква фамилии студента: Ц, Ч, Ш)
1. Из партии, в которой 10 деталей без дефектов и 5 с дефектами, берут наудачу 3 детали. Чему равна вероятность того, что: а) все 3 детали без дефектов; б) по крайней мере, одна деталь без дефектов.
2. В автопробеге участвуют три автомобиля. Первый может сойти с маршрута с вероятностью 0,15; второй и третий не дойдут до финиша, соответственно, с вероятностью 0,05 и 0,1. Требуется определить вероятность того, что до финиша дойдут: а) только один автомобиль; б) два автомобиля; в) по крайней мере, два автомобиля.
3. Часы изготавливаются на трех заводах и поступают в магазин. Первый завод производит 40% продукции, второй - 45%, а третий - 15 %. В продукции первого завода не спешат 80% часов, второго - 70% и третьего- 90%. Какова вероятность того, что купленные часы спешат?
4. Диаметр деталей, изготовленных цехом, является случайной величиной, распределенной по нормальному закону. Дисперсия ее равна 0,0001 см2, математическое ожидание - 2,5 см. В каких границах с вероятностью 0,98 можно гарантировать диаметр детали?
5. Имеются выборочные данные о дневном сборе хлопка (Х, кг):
| Х | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 |
| Число сборщиков |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. В результате специального обследования получено выборочное распределение времени простоя фрезерных станков одного цеха (Х - время простоя, мин; - эмпирические частоты; - теоретические частоты нормального распределения):
| x i | 5,5 | 10,5 | 15,5 | 20,5 | 25,5 | 30,5 | 35,5 |
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака Х генеральной совокупности с эмпирическим распределением выборки.
7. Имеются следующие данные по группе предприятий о выпуске продукции (Х, тыс.шт.) и себестоимости одного изделия (Y, руб.):
| Х | 2,0 | 3,5 | 4,0 | 4,5 | 5,5 | 6,0 |
| Y | 1,9 | 1,7 | 1,8 | 1,6 | 1,5 | 1,4 |
Вычислить коэффициент корреляции на основе этих данных. При уровне значимости 0,05 проверить нулевую гипотезу о равенстве нулю коэффициента корреляции в генеральной совокупности. Построить уравнение линейной регрессионной зависимости и объяснить его смысл. Спрогнозировать среднюю себестоимость одного изделия при выпуске 6,5 тыс. шт.
Вариант № 3
(Первая буква фамилии студента: У, Ф, Х)
1. Партия состоит из 10 деталей I сорта, 7 деталей II сорта и 5 деталей III сорта. Наудачу берутся 2 детали. Какова вероятность того, что детали будут одного сорта?
2. Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго - 0,8, для третьего - 0,9. Найти вероятность того, что: а) все трое промахнутся; б) только один стрелок попадет в цель.
3. Электролампы поставляются магазину тремя заводами. В очередной раз первый завод поставил 100 шт., второй - 150 шт., а третий - 200 шт. Продукция первого завода содержит 97% стандартных ламп, второго - 98%. Продукция третьего завода содержит только стандартные изделия. Определить вероятность того, что купленная в магазине лампа окажется нестандартной.
4. Диаметр стальных стержней, выпускаемых цехом, представляет собой случайную величину, распределенную по нормальному закону с математическим ожиданием 75 мм и средним квадратическим отклонением 0,3 мм. Найти вероятность брака, если допустимые размеры диаметра стержня (75±0,5) мм.
5. Дано распределение времени простоя станка за смену (Х, мин):
| Х | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Число станков |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. В результате обследования получено следующее распределение дневной выручки от продажи продукции в промтоварных магазинах (Х - дневная выручка,руб.; - эмпирические частоты (число магазинов); - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
| x i | |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить гипотезу о нормальном распределении признака Х генеральной совокупности.
7. Определить тесноту связи общего веса некоторого растения (Х, г) и веса его семян (Y, г) на основе следующих выборочных данных:
| Х | |||||||
| Y |
Проверить значимость коэффициента корреляции при a =0,05. Построить линейное уравнение регрессии и объяснить его.
Вариант № 4
(Первая буква фамилии студента: С, Т)
1. Собрание, на котором присутствуют 25 чел., в том числе 9 женщин, выбирает делегацию из трех человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут: а) две женщины и один мужчина; б) хотя бы одна женщина.
2. К испытываемому устройству подключены три прибора. Вероятности выхода из строя прибора, соответственно, равны: 0,3; 0,2; 0,15. Найти вероятность того, что за время проведения испытаний останутся работоспособными: а) один прибор; б) два прибора; в) хотя бы два прибора.
3. Количество продукции, поступающей на механическую обработку от трех литейных цехов, определяется соотношением 3: 4: 5. На 100 единиц продукции первого цеха приходится в среднем 3 единицы брака, второго и третьего цехов, соответственно, 2 и 4 единицы. Наудачу взятая отливка оказалась годной. Какова вероятность того, что она отлита во втором цехе?
4. В некоторой партии гаек средний диаметр оказался равным 82,6 мм, а среднее квадратическое отклонение 1,2 мм. Считая, что размер диаметра гайки подчиняется нормальному закону распределения, найти поле допуска, если брак составляет 1,24%.
5. В результате выборочного обследования получено распределение времени на выполнение технологической операции (Х, с) 20 рабочими:
| Х | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 |
| Число рабочих |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. В результате обследования получено выборочное распределение времени, затрачиваемого операторами бухгалтерских машин на обработку документов складского учета (Х - время, с; - эмпирические частоты (количество документов); - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
| x i | ||||||
|
| ||||||
|
|
Используя критерий Пирсона, при a =0,05 проверить, согласуется ли гипотеза о нормальном распределении признака Х генеральной совокупности с эмпирическим распределением выборки.
7. Представлены данные, отражающие статистическую связь издержек обращения (Y, тыс.руб.) и товарооборота (Х, тыс.руб.):
| Y | 5,0 | 5,2 | 5,8 | 6,4 | 6, 6 | 7,0 |
| Х | 17,6 | 17,5 | 18,0 | 18,1 | 18,2 | 18,5 |
При a = 0,1 проверить значимость указанной статистической связи. Построить уравнение регрессии, объяснить его. Спрогнозировать издержки обращения при заданном товарообороте в 17,9 тыс. руб.
Вариант № 5
(Первая буква фамилии студента: П, Р)
1. Группа студентов-спортсменов, состоящая из 5 студентов II курса и 4 студентов III курса, проводит тренировку. Одновременно тренируются двое. Какова вероятность того, что, войдя случайно на тренировку, мы застанем тренирующимися двух студентов одного курса?
2. Служба контроля качества проверяет партии деталей, изготовленных тремя рабочими. Вероятность того, что будет признана годной партия, изготовленная первым рабочим, составляет 0,97, вторым и третьим рабочим, соответственно, 0,95 и 0,92. Какова вероятность того, что среди партий деталей окажутся забракованными: а) одна партия деталей; б) две партии деталей; в) хотя бы одна партия деталей?
3. На двух станках изготавливают одинаковые детали. Вероятность того, что изготовленная деталь стандартная, для первого станка равна 0,8; для второго - 0,9. Производительность второго станка вдвое больше производительности первого. Найти вероятность того, что взятая наудачу деталь окажется стандартной?
4. Автомат штампует пуговицы. Контролируется диаметр пуговицы - Х, который распределен по нормальному закону с математическим ожиданием 10 мм и средним квадратическим отклонением 0,1 мм. Найти интервал, в котором заключен диаметр изготовленных пуговиц, если брак составляет 1%.
5. Дано распределение расхода сырья, идущего на изготовление одного изделия (Х, г):
| Х | 380-390 | 390-400 | 400-410 | 410-420 | 420-430 |
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. В результате обследования опытных участков одинакового размера получено выборочное распределение урожайности ржи (Х - урожайность, ц/га; - эмпирические частоты; - теоретические частоты, вычисленные в предположении о нормальном законе распределения):
| x i | |||||||
|
| |||||||
|
|
Используя критерий Пирсона, при уровне значимости 0,01 проверить, согласуется ли гипотеза о нормальном распределении признака Х генеральной совокупности с эмпирическим распределением выборки.
7. Имеются выборочные данные о стаже работы (Х, лет) и выработке одного рабочего за смену (Y, шт.):
| Х | ||||||
| Y |
Проверить значимость выборочного коэффициента корреляции при a =0,05. Построить линейное уравнение регрессии и объяснить его. Вычислить предполагаемую среднюю выработку при стаже 5,5 лет.
Вариант № 6
(Первая буква фамилии студента: Н, О)
1. Ящик содержит 10 деталей, среди которых 3 стандартные. Найти вероятность того, что среди отобранных 5 деталей окажутся: а) только 2 стандартные детали; б) все детали нестандартные?
2. На участке установлены три станка. Вероятность выхода из строя первого станка при его включении равна 0,02; второго - 0,03, а третьего - 0,05. Чему равна вероятность того, что при включении одновременно всех станков останутся работоспособными: а) только один станок; б) два станка; в) хотя бы один станок?
3. На склад поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй - 45%, третьей – 35 %. В продукции первой фабрики 5% нестандартных изделий, в продукции второй - 2%, третьей - 1%. Наудачу взятое изделие оказалось стандартным. Найти вероятность того, что оно произведено на первой фабрике.
4. Вес отдельного батона хлеба данной партии есть случайная величина Х, описываемая нормальным законом распределения с математическим ожиданием М(Х) =500 г и средним квадратическим отклонением s(Х) =8 г. Определить вероятность того, что вес взятого наугад из данной партии батона: а) будет в пределах от 496 до 508 г; б) отклоняется от математического ожидание не более чем на 3,2 г.
5. Дано распределение расхода материала на изготовление одного изделия:
| Расход материала, см | 240-250 | 250-260 | 260-270 | 270-280 | 280-290 |
| Число изделий |
Вычислить выборочные среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. Установить при уровне значимости 0,05, случайно или значимо расхождение между эмпирическими и теоретическими частотами, которые вычислены, исходя из предположения, что признак Х распределен нормально:
|
| ||||||||
|
|
7. В результате исследования зависимости выпуска валовой продукции (Y, тыс.руб.) от основных фондов (Х, тыс.руб.) однотипных предприятий получены следующие данные:
| Х | |||||
| Y |
Полагая, что между Х и Y имеет место линейная зависимость, определить выборочный коэффициент корреляции, объяснить его смысл, проверить значимость коэффициента корреляции при уровне значимости 0,05. Построить уравнение регрессии и объяснить его.
Вариант № 7
(Первая буква фамилии студента: Л, М)
1. Из 25 лотерейных билетов 4 выигрышных. Наудачу вынимают три билета. Какова вероятность того, что среди них окажутся: а) не более одного выигрышного билета; б) хотя бы один выигрышный билет?
2. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает: а) только один сигнализатор; б) хотя бы один сигнализатор.
3. На трех поточных линиях производятся одинаковые изделия, которые поступают в службу контроля качества. Производительность первой поточной линии вдвое больше производительности второй и вдвое меньше производительности третьей поточной линии; причем первая линия в среднем производит 50% изделий высшего сорта, вторая - 80%, третья - 30%. Наугад взятое на проверку изделие оказалось высшего сорта. Какова вероятность того, что это изделие произведено на второй поточной линии?
4. Найти дисперсию случайной величины, распределенной по нормальному закону, если известно, что отклонение случайной величины от ее математического ожидания, не превосходящее 0,1, имеет место с вероятностью 0,7887.
5. Имеются выборочные данные о дневном сборе урожая (Х, кг):
| xi | |||||
| Число работников |
Вычислить выборочные среднюю, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
6. Экономический анализ производительности труда предприятий отрасли позволил выдвинуть гипотезу о наличии двух типов предприятий с различной средней величиной показателя производительности труда. Для первой группы (12 объектов) средняя производительность труда в=119 деталей, исправленная выборочная дисперсия 
=126,91; для второй группы (12 объектов), соответственно, 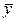в=107 деталей, 
=136,10. Считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y при уровне значимости 0,05 проверить, случайно ли полученное различие средних показателей производительности труда в группах или же имеются два типа предприятий с различной средней величиной производительности труда.
7. Определить тесноту связи выпуска продукции Х (тыс.шт.) и себестоимость одного изделия Y (руб.) на основе следующих данных:
| Х | |||||
| Y |
Проверить значимость выборочного коэффициента корреляции при уровне значимости 0,05. Построить линейное уравнение регрессии и объяснить его.
Вариант № 8
(Первая буква фамилии студента: К)
1. В коробке имеется 7 одинаковых изделий, среди них 4 окрашенных. Наудачу извлекаем 3 изделия. Найти вероятность того, что среди извлеченных трех изделий окажутся: а) только два окрашенных изделия; б) хотя бы одно изделие окрашенное.
2. Вероятность того, что в течение года в радиоприемнике выйдет из строя лампа № 1, равна 0,25. Вероятности выхода из строя ламп №2 и №3 равны, соответственно, 0,15 и 0,1. Найти вероятность того, что вышедший из строя радиоприемник не работает из-за неисправности: а) только одной лампы; б) двух ламп; в) по крайней мере, одной лампы.
3. Среди студентов академии 30% - первокурсники, 35% студентов учатся на втором курсе; на третьем и четвертом курсах их 20% и 15%, соответственно. По данным деканатов известно, что на первом курсе 20% студентов сдали сессию только на "отлично"; на втором - 30%, на третьем - 35%, на четвертом - 40% отличников. Наудачу вызванный студент оказался отличником. Чему равна вероятность того, что он первокурсник.
4. Завод изготавливает шарики для подшипников. Диаметр шарика является случайной величиной, распределенной по нормальному закону с математическим ожиданием 20 см и средним квадратическим отклонением 2 см. В каких границах с вероятностью 0,9216 можно гарантировать размер диаметра шарика?
