Решение нелинейного уравнения 1







Решение нелинейного уравнения 2
(Выполняется по варианту, аналогично примеру раздела 1)
.
Решение системы нелинейных уравнений 3


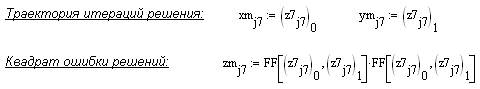


Решение системы нелинейных уравнений 4
(Выполняется по варианту, аналогично разделу 3)
Заключение.
Рассмотрен метод решения нелинейных уравнений и их систем.
Приведенные примеры демонстрируют алгоритм решения, который легко распространяется на системы из трех более уравнений.
Общие особенности метода: необходим подбор начальных приближений решения и итерационного коэффициента (в том числе и знака), что в сложных задачах затрудняет поиск решений.
Существуют более совершенные методы решений, но они имеют относительно сложные алгоритмы.
Методические указания по выполнению работы
Решение нелинейных уравнений методом простой итерации [1, с.21].
Большинство нелинейных уравнений, получаемых в реальных инженерных задачах, не имеет аналитических точных решений. Типичная форма уравнения уравнений имеет вид:
 . (1)
. (1)
Метод простой итерации требует приведения уравнения к следующему виду:
 , (2)
, (2)
что в простейшем случае достигается подстановкой:  .
.
Уравнения (1) и (2) могут иметь одно или несколько решений или не иметь решений.
Метод простой итерации состоит в следующей последовательности действий:
· Задается начальное приближение решения:  .
.
· Вычисляется последовательность приближений решения по формуле:
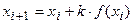 . (3)
. (3)
· Критерием остановки процесса поиска решения может являться либо заданное число шагов итерационного поиска, либо преодоление порога близости к нулю значения левой части уравнения (1).
Итерационный коэффициент  в формуле (3) введен для управления сходимостью итерационной последовательности. Существует пороговое значение коэффициента
в формуле (3) введен для управления сходимостью итерационной последовательности. Существует пороговое значение коэффициента  , разделяющее область сходимости
, разделяющее область сходимости 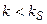 и область расходимости
и область расходимости 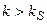 рекуррентной последовательности
рекуррентной последовательности 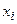 [1, с.23]. Последовательность (3) сходится к искомому решению уравнения (1), если оно существует и функция
[1, с.23]. Последовательность (3) сходится к искомому решению уравнения (1), если оно существует и функция  является непрерывно дифференцируемой.
является непрерывно дифференцируемой.
Начальное приближение решения  может существенно влиять на результат решения: неудачное начальное значение может не позволить методу решить уравнение.
может существенно влиять на результат решения: неудачное начальное значение может не позволить методу решить уравнение.
Проблемными моментами при решении нелинейных уравнений являются выбор начального приближения  и задание итерационного коэффициента сходимости
и задание итерационного коэффициента сходимости  .
.
Решение систем нелинейных уравнений методом итераций осуществляется аналогично приведенному выше алгоритму. Например, для системы трех нелинейных уравнений итерационная последовательность вычисляется следующим образом:
 (4)
(4)
Соотношение (4) является векторной формой формулы (3) и может быть обобщено на любое число неизвестных и уравнений.
Список литературы
1. Охорзин В.А. Прикладная математика в системе MATHCAD. – СПб.: Издательство «Лань». 2008. – 352 c.
2. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. – М.: Высш. шк. 2005. – 544 с.
http://old.teacher.dn-ua.com/old_version/excel/Laba7/part7.htm
ЗАДАНИЕ 7.2. Найти решение нелинейного уравнения.
| № | уравнение | № | уравнение | № | уравнение |

| 
| 
| |||

| 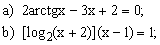
| 
| |||

| 
| 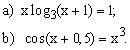
| |||

| 
| 
| |||

| 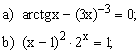
| 
| |||

| 
| 
| |||
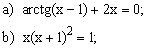
| 
| 
| |||

| 
| 
| |||

| 
| 
|
ЗАДАНИЕ 7.3. Найти решение системы нелинейных уравнений.
| № | Система уравнений | № | Система уравнений | № | Система уравнений |

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||
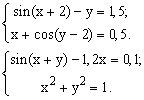
| 
| 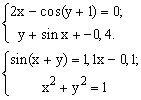
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||
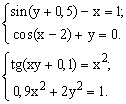
| 
| 
| |||

| 
| 
|






