Задано эмпирическое распределение непрерывной случайной величины X в виде последовательности интервалов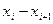 
и соответствующих им частот 
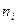, причем 
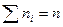(объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина X имеет показательное распределение.
Правило. Для того чтобы при уровне значимости α проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:
1. Найти по заданному эмпирическому распределению выборочную среднюю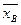 
. Для этого, приняв в качестве «представителя» i-го интервала его середину 
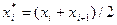, составляют последовательность равноотстоящих вариант и соответствующих им частот.
2. Принять в качестве оценки параметра λ показательного распределения величину, обратную выборочной средней:
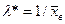
3. Найти вероятность попадания X в частичные интервалы (xi, xi+1) по формуле
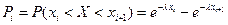
4. Вычислить теоретические частоты:
,
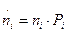где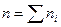 
- объем выборки.
5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы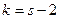 
, где s – число первоначальных интервалов выборки; если же было произведено объединение малочисленных частот, следовательно, и самих интервалов, то s – число интервалов, оставшихся после объединения.
Задача 648. В результате испытания 200 элементов на длительность работы получено эмпирическое распределение, приведенное в табл. 1 (во второй строке указаны интервалы времени в часах, в третьей строке – частоты, т.е. количество элементов, проработавших время в пределах соответствующего интервала).
Таблица 6
| № п/п | ||||||
|
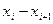
| 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
|
|
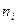
Составим гистограмму.
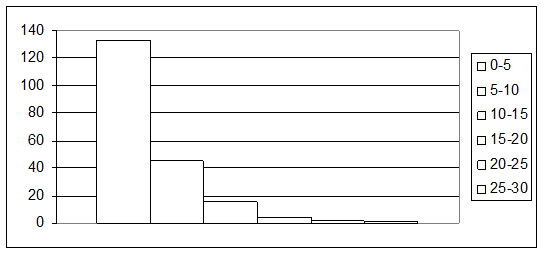
1. Найдем среднее время работы для всех элементов (в качестве среднего времени работы одного элемента примем середину интервала, которому принадлежит элемент):
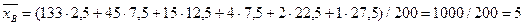
2. Найдем оценку параметра предполагаемого показательного распределения:
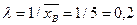
Таким образом, плотность предполагаемого показательного распределения имеет вид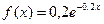 
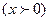
3. Найдем вероятности попадания X в каждый из интервалов по формуле
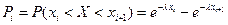
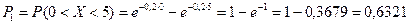
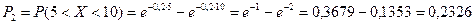
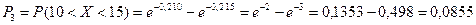
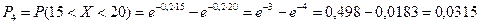
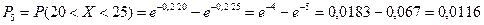
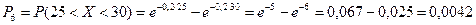
4. Найдем теоретические частоты: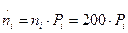 
, где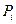 
- вероятность попадания X в i-й интервал.
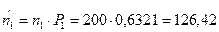
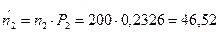
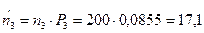
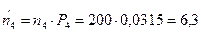
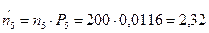
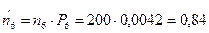
5. Сравним эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого составим расчетную таблицу, причем объединим малочисленные частоты (4+2+1=7) и соответствующие им теоретические частоты (6,30+2,32+0,84=9,46)
Таблица 7
| 
| 
| 
| 
|  
|
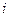
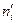
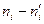
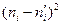
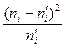
| 126,42 | 6,58 | 43,2964 | 0,3425 | ||
| 46,52 | -1,52 | 2,3104 | 0,0497 | ||
| 17,10 | -2,10 | 4,4100 | 0,2579 | ||
| 9,46 | -2,46 | 6,0516 | 0,6397 | ||
| Σ | 
| 
|
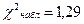
Замечание: Для упрощения вычислений в случае объединения малочисленных частот целесообразно объединить и сами интервалы, которым принадлежат малочисленные частоты в один интервал. Так, в рассматриваемой задаче, объединив последние три интервала, получим один интервал (15,30). В этом случае теоретическая частота
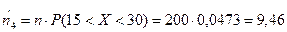
совпадает с суммой теоретических частот (9,46).
По таблице критических точек распределения χ2, по уровню значимости α=0,05 и числу степеней свободы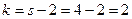 
находим критические области χкр2(0,05;2)=6,0.
Так как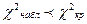 
– то нет оснований отвергнуть гипотезу о распределении X по показательному закону. Другими словами, данные наблюдений согласуются с этой гипотезой.
Задача
Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х c эмпирическим распределением выборки объема n=100, приведенным в табл. 8
| Номер интервала i | Граница интервала | Частота ni | |
| xi | xi+1 | ||
| n=100 |
Составим гистограмму
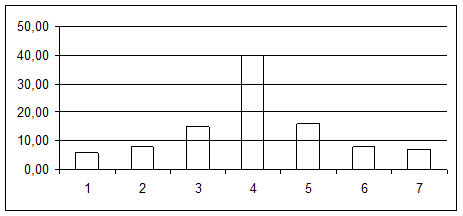
Решение
1. Вычислим выборочную среднюю и выборочное среднее квадратическое отклонение методом произведений. Для этого перейдем от заданного интервального распределения к распределению равноотстоящих вариант, приняв в качестве варианта xi* среднее арифметическое концов интервала: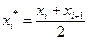 
. В итоге получим распределение:
| xi* | 5,5 | 10,5 | 15,5 | 20,5 | 25,5 | 30,5 | 35,5 |
| ni |
Вычислив выкладки по методу произведений найдем выборочную среднюю и выборочное среднее квадратическое отклонение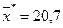 
, σ*=7,28.
Для вычисления составим таблицу и вычислим по формулам
Таблица 9
| № | Границы | Частота, ni |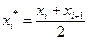
| ni· xi* | ni2 | ni2· xi* | |
| xi | xi+1 | ||||||
| 5,5 | |||||||
| 10,5 | |||||||
| 15,5 | 232,5 | 3487,5 | |||||
| 20,5 | |||||||
| 25,5 | |||||||
| 30,5 | |||||||
| 35,5 | 248,5 | 1739,5 | |||||
| Σ |
2. Найдем интервалы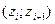 
учитывая что ; 
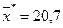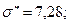
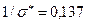. Для этого составим расчетную таблицу (левый конец первого интервала примем равным -∞, а правый конец последнего ∞).
Таблица 10
| i | Границы |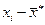 
| 
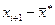
| Границы интервала | ||
| 
| 
| 
| |||
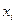
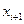
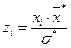
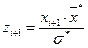
| - | -12,7 | -∞ | -1,74 | |||
| -12,7 | -7,7 | -1,74 | -1,06 | |||
| -7,7 | -2,7 | -1,06 | -0,37 | |||
| -2,7 | 2,3 | -0,37 | 0,32 | |||
| 2,3 | 7,3 | 0,32 | 1,00 | |||
| 7,3 | 12,3 | 1,00 | 1,69 | |||
| 12,3 | - | 1,69 | -∞ |
3. Найдем теоретические вероятности 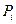и теоретические частоты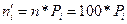 
Для этого составим расчетную таблицу №2.
Таблица №11
| i | Границы интервала |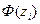 
| 
| 
| 
| |||
| 
| |||||||
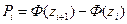
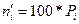
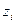
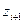
| - | -1,74 | -0,5000 | -0,4591 | 0,0409 | 4,09 | |||
| -1,74 | -1,06 | -0,4591 | -0,3554 | 0,1037 | 10,37 | |||
| Продолжение таблицы 11 | ||||||||
| -1,06 | -0,37 | -0,3554 | -0,1443 | 0,2111 | 21,11 | |||
| -0,37 | 0,32 | -0,1443 | 0,1255 | 0,2698 | 26,98 | |||
| 0,32 | 1,00 | 0,1255 | 0,3413 | 0,2158 | 21,58 | |||
| 1,00 | 1,69 | 0,3413 | 0,4545 | 0,1132 | 11,32 | |||
| 1,69 | - | 0,4545 | 0,5000 | 0,0455 | 4,55 | |||
| Σ | ||||||||
4. Сравним эмпирические и теоретические частоты, используя критерии Пирсона:
а) Вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу №3.
Таблица №12
| i |
|
| 
| 
| 
| 
| 
|
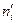
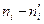
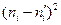
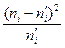
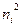
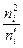
| 4,09 | 1,91 | 3,6481 | 0,8920 | 8,8019 | |||
| 10,37 | -2,37 | 5,6169 | 0,5416 | 6,1716 | |||
| 21,11 | -6,11 | 37,3321 | 1,7684 | 10,6584 | |||
| 26,98 | 13,02 | 169,5204 | 6,2833 | 59,3052 | |||
| 21,58 | -5,58 | 31,1364 | 1,4428 | 11,8628 | |||
| 11,32 | -3,32 | 11,0224 | 0,9737 | 5,6537 | |||
| 4,55 | 2,45 | 6,0025 | 1,3192 | 10,7692 | |||
| Σ |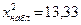 
| 113,22 |
Столбцы 7 и 8 служат для контроля вычислений по формуле
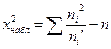
Контроль: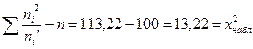 
Вычисления произведены правильно.
5) По таблице критических точек распределения x2 по уравнению значимости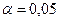 
и числу степеней свободы 
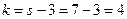(s-число интервалов) находим критическую точку правосторонней критической области 
.
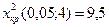Так как 13,33>9,5 (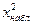
> 
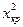) – отвергаем гипотезу о нормальном распределении генеральной совокупности 
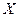. Данные наблюдений не согласуются с гипотезой.
