У таблиці 1 дана вибірка
Таблица 1 – Вихідні дані
| ||||||||||
| 7,5 | 6,9 | 6,1 | 5,2 | 4,6 | 3,7 | 2,9 | 1,7 | 1,2 | 0,9 |
Побудуємо графік точкової функції:
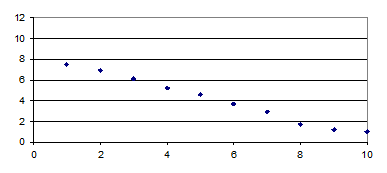
Рис. 1. Графік залежності 
від 
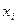
За розташуванням точок є можливість передбачити наявність лінійної кореляційної або регресійної залежності. Будемо шукати рівняння регресії у виді: 
Для визначення коефіцієнтів використовуємо метод найменших квадратів, згідно з яким:
Після нескладних перетворень отримаємо
(1)
где 
, 
. 
. 
Коефіцієнт b називається коефіцієнтом регресії. Вираз у чисельнику для b є коваріацією (кореляційний момент) величин У та Х, який характеризує ступінь розсіювання навколо середнього значення:
Складемо таблицю 2 та обчислимо вибіркові середні.
Таблиця 2 – Визначення вибіркових середніх значень
|
|
| 
| 
|
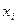
| 7,5 | 1,00 | 7,50 | |
| 6,9 | 4,00 | 13,80 | |
| 6,1 | 9,00 | 18,30 | |
| 5,2 | 16,00 | 20,80 | |
| 4,6 | 25,00 | 23,00 | |
| 3,7 | 36,00 | 22,20 | |
| 2,9 | 49,00 | 20,30 | |
| 1,7 | 64,00 | 13,60 | |
| 1,2 | 81,00 | 10,80 | |
| 0,9 | 100,00 | 9,00 | |
| 
| 
| 
|
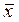
| 5,5 | 4,07 | 38,50 | 15,93 |
Обчислимо коефіцієнти за формулою (1):
Дисперсії змінних Х та Y визначаються за формулами
,
sх та sy називають середніми квадратичними відхиленнями.
Коефіцієнт кореляції визначається за формулою: 
При r>0 кореляційний зв'язок між змінними – прямий, при r<0 – зворотній.
Доповнимо таблицю двома стовпцями та обчислимо дисперсії.
Таблиця 3 – Остаточний варіант таблиці
|
|
|
|
| 
| 
|
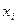
| 7,5 | 1,00 | 7,50 | 20,25 | 11,76 | |
| 6,9 | 4,00 | 13,80 | 12,25 | 8,01 | |
| 6,1 | 9,00 | 18,30 | 6,25 | 4,12 | |
| 5,2 | 16,00 | 20,80 | 2,25 | 1,28 | |
| 4,6 | 25,00 | 23,00 | 0,25 | 0,28 | |
| 3,7 | 36,00 | 22,20 | 0,25 | 0,14 | |
| 2,9 | 49,00 | 20,30 | 2,25 | 1,37 | |
| 1,7 | 64,00 | 13,60 | 6,25 | 5,62 | |
| 1,2 | 81,00 | 10,80 | 12,25 | 8,24 | |
| 0,9 | 100,00 | 9,00 | 20,25 | 10,05 | |
|
|
|
|
| 
| 
|
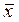
| 5,5 | 4,07 | 38,50 | 15,93 | 8,25 | 5,09 |
Обчислимо коефіцієнт кореляції
Після того, як знайдено рівняння лінійної регресії, проведемо оцінку значущості як рівняння в цілому, так і окремих його параметрів.
Коефіцієнт детермінації R 2= r2 .
Оцінка значущості рівняння регресії в цілому дається за допомогою F- критерію Фішера. При цьому висувається нульова гіпотеза Ho, що коефіцієнт регресії дорівнює нулю, тобто b = 0, і, отже, чинник х не робить впливу на результат у. Для цього порівнюють фактичне значення Fфакт та критичне (табличне) Fтабл значення F – критерію, при цьому Fфакт обчислюється за формулою 
Після обчислення цієї величини проводиться тест, який полягає в перевірці гіпотези Hо про статичну не значущість рівняння регресії. Рівень значущості a – це ймовірність відкинути правильну гіпотезу за умови, що вона вірна. Приймаємо a=0,05. Якщо Fтабл<Fфакт, то гіпотеза про випадкову природу оцінюваних характеристик відхиляється і признається статистична значущість і надійність рівняння регресії. Табличне значення вибирається із спеціальної таблиці з урахуванням того, що к1=1 к2=n-2.
Із таблиці визначимо Fтабл (при к1=1, к2 = 8, рівень значущості a=0,05). Значення Fтабл = 5,32. У нашому випадку Fтабл =5,32 < Fфакт = 1136,503.
Це означає, що гіпотеза Но про випадкову природу оцінюваних характеристик відхиляється і признається значущість рівняння регресії. Для оцінки статистичної значущості коефіцієнтів регресії і кореляції розраховуються t- критерій Ст’юдента та довірчі інтервали для кожного з показників. Висувається гіпотеза Hо про випадкову природу показників.
 |
Випадкові помилки параметрів обчислюються за формулами:
Якщо tтабл < tфакт, то Но відхиляється,тобто a, br відрізняються від нуля і сформувалися під впливом діючого чинника x. Для розрахунку довірчого інтервалу визначаємо граничні помилки.
 |
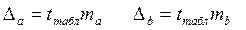Тоді довірчі інтервали мають вид:
Обчислення стандартних помилок – досить трудомісткий процес, тому для визначення 
використовуємо вбудовану функцію Excel ЛИНЕЙН(). Для цього введемо таблицю 1 на робочому листі (починаючи з чарунку А1), а потім помітимо область чарунків А12:В16, для чого клацнемо по значку вибору функцій, виберемо категорію "Статистические" та знайдемо функцію ЛИНЕЙН(). З'явиться вікно, в якому необхідно вказати інтервал значень 
. У полях "Конст" та "Статистика" введемо цифру 1. На рисунку 2 представлено заповнене вікно.
Рис 2. Введення аргументів функції ЛИНЕЙН()
Натиснемо ОК, потім клавішу F2, потім Enter при натиснутих одночасно Shift и CTRL. У поміченої області з'являться результати розрахунку (таблиця 4).
Таблиця 4 – Результати розрахунку
| -0,78242 | 8,373333 |
| 0,023209 | 0,144008 |
| 0,99301 | 0,210807 |
| 1136,503 | |
| 50,50548 | 0,355515 |
Проаналізуємо результати. У першому рядку таблиці отримані коефіцієнти b та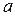 
, тобто b= - 0,78242; 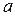= 8,37333. У другому рядку таблиці підраховані стандартні помилки mb =0,023209; ma = 0,144008.
Коефіцієнт детермінації R2 = 0,99301 вказано в третьому рядку, першого стовпця. Fфакт = 1136,503 (четвертий рядок, перший стовпець), число ступенів свободи дорівнює n-2=8 (четвертий рядок, другий стовпець).
Стандартна помилка Y дорівнює 0,210807 (третій рядок, другий стовпець). Нарешті, регресійна і залишкова суми квадратів представлена в нижньому рядку. Таким чином, рівняння парної регресії має вид:
y =8,37733 –0,78242 x
Рис. 3. Графік регресійної прямої
Оцінимо якість рівняння регресії, значущість коефіцієнтів і визначимо довірчі інтервали.
tb =-0,78242/0,023209=-33,7; ta = 8,37333/0,144008=58,14
Табличне значення tтабл = 2,306 (при рівні значущості a=0,05 та k=8). Табличне значення буде менше ta, tb, тому коефіцієнти рівняння регресії статистично значимі. Граничні помилки рівні:
Da = 2.306*0,144008=0,332 Db = 2.306*0,023209= 0,0535
Отже, довірчі інтервали коефіцієнтів рівняння мають вид:
8,04 £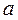 
£ 8,705 -0,8359£ b £ -0,7289
