Поиск:

Полиномиальное приближение

Рассмотрим квадратичную модель, в которой функция регрессии представляет собой полином второй степени. Уравнение регрессии квадратичной модели имеет следующий вид.

В качестве независимых переменных в уравнении используются переменные x и x ².

Построить график для каждого вида регрессионной модели

Всего должно быть построено пять графиков: линейный, полиномиальный, степенной, логарифмический, экспоненциальный. На графике необходимо указать вид уравнения и коэффициент детерминации R².

Построить сравнительную таблицу

Вид сравнительной таблицы.

№	Наименование регрессионной модели	Вид регрессионной модели	Коэффициент детерминации R²

Сделать вывод

Указывается, какая из регрессионных моделей лучше аппроксимирует связь между двумя рядами случайных величин.

Часть 2 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА

1. Определить реалистичное содержание целевой функции

(Целевая функция, функцию отклика, зависимая переменная, реакция системы на воздействие факторов, содержание целевой функции) Y - ________________________

Проходка за рейс

2. Определить реалистичное содержание (сущность) факторов

(Независимые переменные, от которых зависит целевая функция) Содержание факторов X₁- _{______________________________________} X₂- _{______________________________________} X₃- _{______________________________________}

Скорость вращения долота, Осевое усилие

3. Определить уровни варьирования значений факторов

Минимальное значение каждого фактора Х_i_min = ____________ Максимальное значение каждого фактора X_i_max= ____________

4. Определить среднее значение фактора

Среднее значение фактора определяется по формуле

. X_1ср= __________ X_2ср = __________ X_3ср = __________

5. Определить интервал варьирования фактора

Интервал варьирования определяется по формуле: dx_i = X_{i 0} – X_{i min} = X_{i max}- X_{i 0}. = ___________

6. Проверить корректность определения значений факторов

Для этого необходимо составить таблицу натуральных значений факторов

Фактор	X₁	X₂	X₃
Минимальное значение, Х_i_min«- 1»
Максимальное значение, X_i_max«+ 1»
Среднее значение, X_i_ср
Интервал варьирования dХ_i

7. Определить нормированные значения факторов

Нормированные значения определяются формулой

8. Составить матрицу планирования эксперимента (полный факторный)

Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.

Номер опыта	Нулевой фактор	Кодовый (нормированный) масштаб
Х_0н	Х_1н	Х_2н	Х_1нХ_2н
	+1	-1	-1	+1
	+1	+1	-1	-1
	+1	-1	+1	-1
	+1	+1	+1	+1

В примере, показанном ниже, рассматривается только два фактора.

9. Определение необходимого числа параллельных опытов

Рекомендуется проводить по каждому опыту равномерное количество дублирующих опытов. В общем случае их должно быть не менее 3…5. Провести по 5 параллельных опытов на каждую комбинацию факторов

10. Провести факторный эксперимент

Определить численные значения функции отклика в зависимости от комбинации значений факторов и составить матрицу с результатами экспериментов

Номер опыта	Нормированные значения факторов	Параллельные опыты
j	х_0н	х_1н	х_2н	х_1нх_2н	y_1j	y_2j	y_3j	y_4j	y_5j
	+1	-1	-1	+1
	+1	+1	-1	-1
	+1	-1	+1	-1
	+1	+1	+1	+1

j	X₀	X₁	X₂	X₁X₂	Y₁_j	Y₂_j	Y₃_j
	+1	-1	-1	+1
	+1	+1	-1	-1
	+1	-1	+1	-1
	+1	+1	+1	+1

11. Вычислить среднее значение функции отклика

(1) при m - число повторных опытов

Среднее значение выходной величины Y_i в каждой точке определим по формуле (1) при (m = 3) Y₁ = (43+35+48)/3 = 42 Y₂ = (90+86+94)/3 = 90, Y₃ = (10+16+16)/3 = 14, Y₄ = (56+54+58)/3 = 56

12. Вычислить дисперсию среднего арифметического для каждой строки матрицы эксперимента

m – количество параллельных опытов в строке матриц

Определим по формуле (2) построчную дисперсию S²{y₁}= [(43–42)² +(35–42)² + (48–42)²]/2 = 43, S²{y₂}= [(90–90)² +(86–90)² + (94–90)²]/2 = 16, S²{y₃}= [(10–14)² +(16–14)² + (16–14)²]/2 = 12, S²{y₄}= [(56–56)² +(54–56)² + (58–56)²]/2 = 4.

13. Составить таблицу расчета дисперсий

Номер опыта	Значение функции отклика, y_i_j	Среднее значение функции отклика y_ср	Дисперсия опыта, s²_yi
y₁	y₁	y₁	y₁	y₁

Номер опыта	y₁	y₁	y₁	Среднее значение функции отклика, y_j	Дисперсия опыта, s²{y_j}

Проверить однородность дисперсии с помощью критерия Кохрена

Критерий (коэффициент) Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них. Определить критерий Кохрена по формуле

где s_max – наибольшая величина дисперсии; s_i – дисперсия i-го опыта N – общее число опытов в матрице. В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N, где N – число опытов (количество строк в матрице планирования)

выбрать среди всей совокупности рассчитанных построчных дисперсий число с максимальной дисперсией

S²{y_i}мах

вычислить сумму всех построчных дисперсий

ΣS²{y_i}

вычислить отношение максимальной дисперсии к сумме всех построчных дисперсий: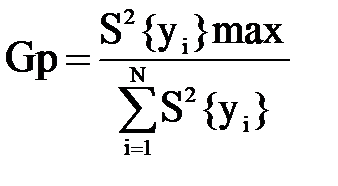

По данным из нашего примера определим расчетное значение коэффициента Gp = 43/(43+16+12+4) = 0,57.

Задать уровень значимости

Для инженерных задач достаточен уровень значимости a = 0,05

Определить степени свободы

степени свободы числителя (f₁) f₁= m –1 m – количество параллельных опытов в строке матриц степень свободы знаменателя (f₂) f₂ = N. N – общее число опытов в матрице

Cравнить расчетное значение коэффициента Кохрена с табличным значением Найти значение f₁ в горизонтальном заголовке таблицы (выбирается столбец), Найти значение f₂ выбирается слева в вертикальном заголовке таблицы (выбирается строка) Установить табличное величину критерия Gт на пересечении выбранных столбца и строки

В соответствии с таблицей коэффициентов для a = 0,05; f₁ = 3 – 1 = 2; f₂ = 4, Gт = 0,77

Если выполняется условие: Gp < Gт, то с достоверностью 1 – a все построчные дисперсии признаются однородными. В противном случае гипотезу отвергают.

Gт = 0,77; Gт > Gp, т.е. условие выполняется

14. Выбрать вид уравнения регрессии (модели отклика)

Рекомендуется линейная модель Y = b₀ X₀ + b₁X₁ + b₂X₂; Y = b₀ X₀ + b₁X₁ + b₂X₂ +b₁₂X₁Х₂; (Х₀=1).

15. Вычислить коэффициенты регрессии

16.Проверить статистическую значимость коэффициентов регрессии

Оценка производится по t-критерию Стьюдента. Т.е. проверяется отклонение от нуля найденной оценки. Для каждого коэффициента b_kвычисляется коэффициент Стьюдента:

где b_k – коэффициент уравнения регрессии S{b_k} – оценка среднего квадратичного отклонения погрешности определения коэффициента.

Определить оценку генеральную дисперсию воспроизводимости

Оценкой дисперсии воспроизводимости S²_в, характеризующая точность одного измерения, является средняя из всех построчных дисперсий

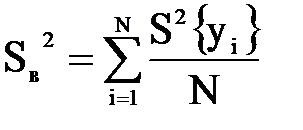
S²_в = (43 + 16 + 12 + 4)/4 = 18,75

Определитьдисперсию коэффициентов, найденных по экспериментальным данным

S²{b_k} = 18,75/(4*3)= 1,56

Выполнить оценкудисперсию коэффициентов, найденных по экспериментальным данным

Оценка

Для рассматриваемого примера S{b_k} = 1,25.

Вычислить критерий Стьюдента

Определим расчетные значения коэффициента Стьюдента t₀ = 50,5/1,25 = 40,4; t₁ = 22,5/1,25 = 18; t₂ = 15,5/1,25 = 12,4; t₁₂ = 1,5/1,25 = 1,2.

Выбрать уровень статистической значимости

a = 0,05

Определить число степеней свободы

f = N (m – 1)

f = 4 (3 – 1) = 8

Найти табличное значение коэффициента Стьюдента

При выбранном уровне статистической значимости a по таблицам распределения Стьюдента при числе степеней свободы f = N (m – 1) находят табличное значение коэффициента t_табл.

Из таблиц при уровне статистической значимости a = 0,05 и числе степеней свободы f = 4 (3 – 1) = 8, табличное значение коэффициента равно t_т = 2,3.

Сравнить табличное значение с расчетным

Если выполняется неравенство t_табл > t_k, то принимается нуль-гипотеза, т.е. считается, что найденный коэффициент a_k является статистически незначительным и его следует исключить из уравнения регрессии.

Сопоставление расчетных значений t_k с табличным t_т. Неравенство выполняется для t₁₂. Следовательно, можно предположить, что a₁₂ статистически незначим и его можно исключить из уравнения регрессии

Составить уравнение регрессии с учетом статистической значимости коэффициентов

Y = b₀ X_0н + b₁X_1н + b₂X_2н

Уравнение регрессии, содержащее статистически значимые коэффициенты, будет (в кодированной системе) Y' = 50,5 + 22,5x₁ – 15,5x₂.

Проверить адекватность модели (пригодность для практического применения)

Полученное уравнение регрессии необходимо проверить на адекватность исследуемому объекту.

Проверка адекватности выполняется по критерию Фишера Для этой цели необходимо оценить, насколько отличаются средние значения y_i выходной величины, полученной в точках факторного пространства, и значения y_i, полученного из уравнения регрессии в тех же точках факторного пространства. Адекватность модели проверяют по критерию Фишера F- критерию Fp= S²_ад/S²_в

Определить значения функции отклика по уравнению регрессии

Для рассматриваемого примера получаем: Y'₁ =50,5 +22,5 (–1) – 15,5 (–1) = 43,5; Y'₂ =50,5 +22,5 (+1) – 15,5 (–1) = 88,5; Y'₃ =50,5 +22,5 (–1) – 15,5 (+1) = 12,5; Y'₄ =50,5 +22,5 (+1) – 15,5 (+1) = 57,5

Определить оценку дисперсию адекватности

, где L – число значимых коэффициентов.

Рассчитаем оценку дисперсии адекватности: S²_ад = 3[(42 – 43,5)² + (90 – 88,5)² + (14 – 12,5)² + (56 – 57,5)²]/(4 – 3) = 27

Определить оценку генеральную дисперсию воспроизводимости

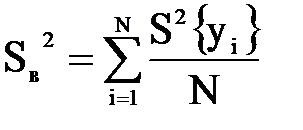
S²_в = (43 + 16 + 12 + 4)/4 = 18,75

Задать уровень значимости

a = 0,05

Вычислить критерий Фишера

Fp= S²_ад/S²_в

Fp = S²_ад/S²_в = 27/18,75 = 1,44.

Определить число степеней свободы

f_ад = N – l f_в = N(m - 1)

f_ад = (4 – 3) = 1 и f_в= 4 (3 – 1)=8

Найти табличные значения F- критерию

Найденное расчетным путем Fp сравнивают с табличным значением Fт,которое определяется при уровне значимости a и числе степеней свободы f_ад = N – l - по горизонтали (f₂) f_в = N(m - 1) – по вертикали (f₁)

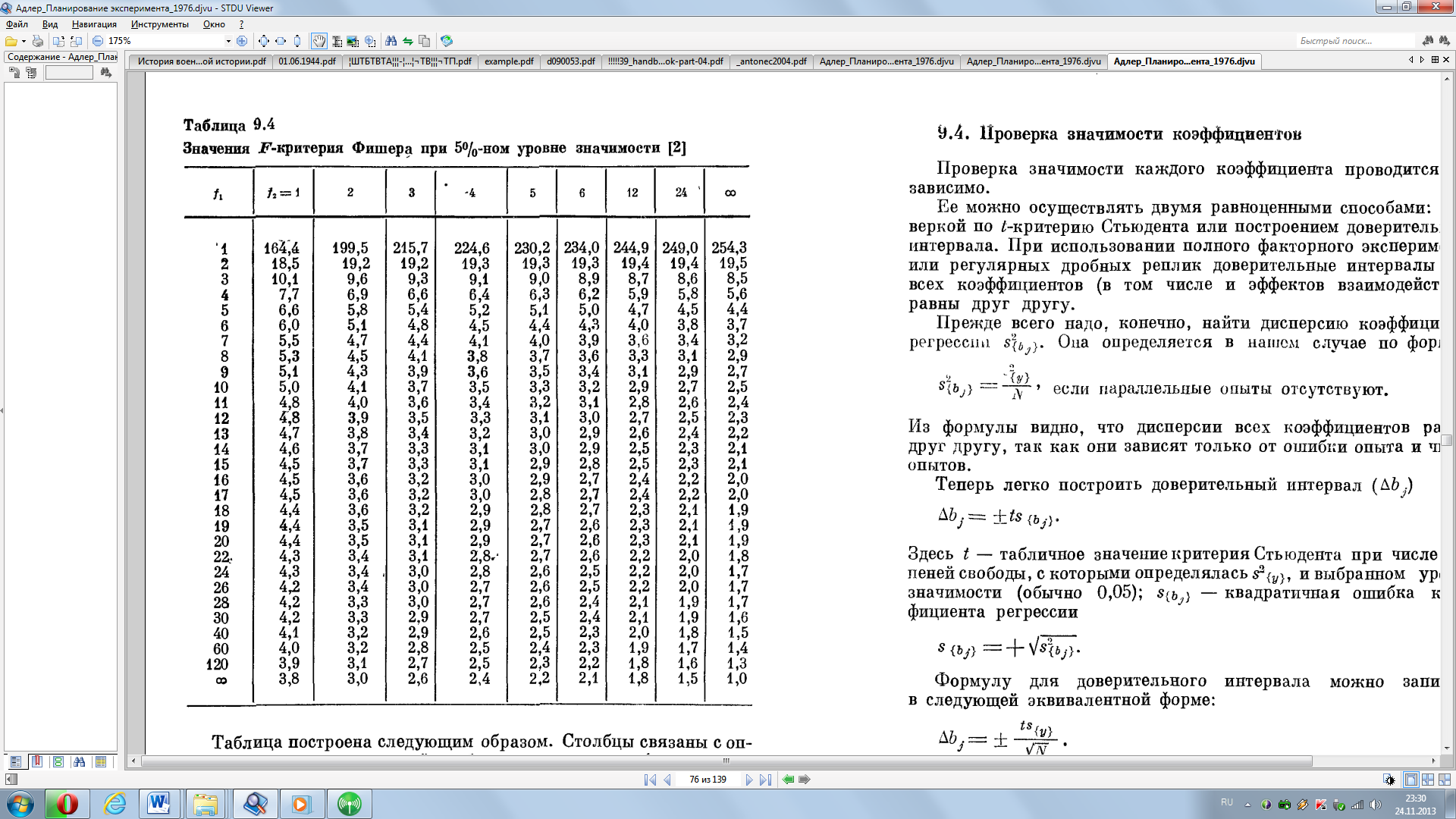
Табличное значение коэффициента Фишера при уровне статистической значимости a =0,05 и числе степеней свободы f_ад = (4 – 3) = 1 и f_в= 4 (3 – 1)=8 будет Fт=5,32

Сравнить расчетное значение критерия с табличным и сделать вывод об адекватности модели

Если Fp < Fт, то полученная математическая модель с принятым уровнем статистической значимости a адекватна экспериментальным данным

Следовательно, при выбранном уровне статистической значимости полученная в результате эксперимента регрессионная модель вида y' = 50,5 + 22,5x₁ – 15,5x₂ адекватна исследуемому объекту

17. Преобразовать уравнение регрессии в нормированных значениях факторов в уравнение с натуральными значениями факторов

Подставить в уравнение регрессии значения факторов в натуральных значениях по формуле Y = b₀ + b₁

+ b₂

+b₁₂

18. Оформить отчет по результатам работы

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА 1. Титульный лист, содержащий информацию о студенте (группа, фамилия, номер варианта); 2. Результаты подготовки (выбранные по варианту значения экспериментальных данных); 3. Основные теоретические положения (используемые формулы); 4. Результаты подготовки (матрица планирования в виде таблицы); 5. Листинг программы (язык программирования не имеет значения); 6. Ответы на контрольные вопросы; 7. Результат выполнения работы; 8. Выводы по лабораторной работе.

Основная учебная литература

1. Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных: учебн. пособ. / Н.И. Сидняев. – М.: Изд-во Юрайт, 2011.- 399с.

2.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб.пособ.-12-е изд., перераб. / В.Е. Гмурман.- М.: Изд-во Юрайт, 2010.- 479с.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособ. -12-е изд., перераб. / В.Е. Гмурман. – М.: Высшобраз.,2006. – 476с.

4 Боровков, А.А. Математическая статистика: Учебник / А. А. Боровков. – Изд. 4-е, стер. – Санкт-Петербург; М.; Краснодар: Лань, 2010. – 703 с.. (электронный ресурс).

Дополнительная учебная и справочная литература.

5 Короткова, Е. И. Планирование и организация эксперимента: учебное пособие [для хим. специальностей вузов] / Е. И. Короткова; Федер. агентство по образованию, Гос. образоват. учреждение высш. проф. образования, «Нац. исслед. Томск. политехн. ун-т». – Томск: Изд-во Том. политехн. ун-та, 2010. – 123 с.: a-ил.

6 Организация и планирование эксперимента: метод. указания к курсовой работе студентов специальности 150102 «Металлургия цв. металлов» оч. формы обучения / Иркут. гос. техн. ун-т; сост. О. В. Белоусова, Е. Г. Садохина. – Иркутск: Изд-во ИрГТУ, 2009. – 28 с.:

7 Организация и планирование эксперимента: программа, метод. указания и контр. работы для специальности 150102 «Металлургия цв. металлов» оч. формы обучения / Иркут. гос. техн. ун-т; сост. О. В. Белоусова, В. И. Щепин. – Иркутск: Изд-во ИрГТУ, 2009. – 35 с.: a-ил.

8 Альбом наглядных пособий по общей теории статистики: учеб. пособие для высш. с.-х. учеб. заведений по экон. спец. / С.С. Сергеев. – М.: Финансы и статистика, 1991. – 79 с.: a-ил.

9 Айвазян, С. А. Прикладная статистика в задачах и упражнениях:Учеб. для экон. специальностей вузов / С. А. Айвазян, В. С. Мхитарян. – М.: ЮНИТИ-Дана, 2001. – 270 с.: a-ил.

10 Афанасьева, Н. Ю. Вычислительные и экспериментальные методы научного эксперимента: Учеб. Пособие. / Н. Ю. Афанасьева. – М.: КНОРУС, 2010. – 330 с.: a-ил.

11 Барра, Ж.-Р. Основные понятия математической статистики/ Ж.-Р. Барра; пер. с фр. Ж-Р Барра. – М.: Мир, 1974. – 275 с.

12 Математическая статистика в разведочном бурении: справ.пособие / Рубен Александрович Ганджумян. – М.: Недра, 1990. – 224 с.: a-ил.

13 Горелова, Г. В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel: учеб.пособие / Г. В. Горелова, И. А. Кацко. – [2-е изд., испр. и доп.]. – Ростов н/Д: Феникс, 2002. – 395 с.

14 Вычисления в MathCAD / Д. А. Гурский. – Минск: Новое знание, 2003. – 813 с.: a-ил.

15 Ликеш И. Основные таблицы математической статистики / Иржи Ликеш; Перевод с чеш. Ю. А. Данилова. – М.: Финансы и статистика, 1985. – 356 с.: a-ил.

16 Математическая статистика на персональном компьютере (на основе программы MicrosoftExcel): практикум для студентов фак. технологии и компьютеризации машиностроения / сост. Г. Д. Гефан; Иркут.гос. техн. ун-т. – Иркутск: ИрГТУ, 2000. – 20 с.: a-ил. – (Высшая математика).

17 Сидняев, Н. И. Теория планирования эксперимента и анализ статистических данных: учебное пособие для магистров по специальности «Прикладная математика» / Н. И. Сидняев. – Москва: Юрайт, 2011. – 399 с.: a-ил.

1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.

2. Асатурян В.И. Теория планирования эксперимента: Учеб. пособие для втузов. М.: Радио и связь, 1983.

3. Налимов В.В. Теория эксперимента. М.: Наука, 1971.

4. Планирование и организация измерительного эксперимента / Е.Т. Володаpский, Б.Н. Малиновский, Ю.М. Туз.-К.: В.ш. Головное изд-во, 1987.

ВАРИАНТ 1

Sгл - глинистость,

К кар ~ карбонатность.

№ п.п.	S_ГЛ%	Ккар%
1.
1.		13,2
2.
3.
4.	31,5
5.	23,0
6.	25,0
7.
8.
9.
10.
11.
12.	35,6
13.
14.
15.
16.
17.
18.
19.		13,2
20.
21.
22.	31,5
23.	23,0
24.	25,0
25.

26.
27.
28.
29.
30.	35,6
31.
32.
33.
34.
35.
36.
37.		13,2
38.
39.
40.	31,5
41.	23,0
42.	25,0
43.
44.
45.
46.
47.
48.	35,6
49.
50.

ВАРИАНТ 2

Кпес. - песчанистость,

Ккар ~ карбонатность.

№ п.п.	Ккар%	Кпес. %
1.
2.	13,2
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.	13,2
21.
22.
23.
24.
25.

26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.	13,2
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.

ВАРИАНТ 3

Кпор - пористость,

Кпр - проницаемость,

№ п.п.	Кпор%	Кпр * 10^-15м2
1.
2.	24,7
3.	26,2
4.	25,8
5.	25,8
6.	25,8
7.	26.9
8.	25,9
9.	22,6
10.	24,4
11.	25,1
12.	24,9
13.	24,8
14.	24,4
15.	25,0
16.	24,3
17.	23,8
18.	22,4
19.
20.	24,7
21.	26,2
22.	25,8
23.	25,8
24.	25,8
25.	26.9

26.	22,6
27.	24,4
28.	25,1
29.	24,9
30.	24,8
31.	24,4
32.	25,0
33.	24,3
34.	23,8
35.	22,4
36.
37.	24,7
38.	26,2
39.	25,8
40.	25,8
41.	25,8
42.	26.9
43.	25,9
44.	22,6
45.	24,4
46.	25,1
47.	24,9
48.	24,8
49.	24,4
50.	25,0

ВАРИАНТ 4

Sгл - глинистость,

Кпр - проницаемость,

№ п.п.	S_ГЛ%	Кпр * 10^-15м2
1.
2.
3.
4.
5.	31,5
6.	23,0
7.	25,0
8.
9.
10.
11.
12.
13.	35,6
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.	31,5
24.	23,0
25.	25,0

26.
27.
28.
29.
30.
31.	35,6
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.	31,5
42.	23,0
43.	25,0
44.
45.
46.
47.
48.
49.	35,6
50.

Вариант 5.

№ п/п	Агрегат в работе %	Коэф. готовности
1.
2.
3.
4.
5.
6.	2,5
7.	9,7	0,2
8.		5,6
9.
10.
11.	26,3	66,3
12.	7,6
13.	10.66
14.	6,1	86,3
15.
16.
17.
18.
19.
20.	2,5
21.	9,7	0,2
22.		5,6
23.
24.

25.	26,3	66,3
26.	7,6
27.	10.66
28.	6,1	86,3
29.
30.
31.
32.
33.
34.	2,5
35.	9,7	0,2
36.		5,6
37.
38.
39.	26,3	66,3
40.	7,6
41.	10.66
42.	6,1	86,3
43.
44.
45.
46.
47.
48.	2,5
49.	9,7	0,2
50.		5,6

Вариант 6

№ п/п	агрегат в резерве, %	Кол-во вынужденных отказов
1.
2.
3.
4.
5.
6.
7.	9,9
8.
9.
10.
11.
12.	91,3	-
13.	84.5
14.
15.
16.
17.
18.
19.
20.
21.	9,9
22.
23.
24.

25.
26.	91,3	-
27.	84.5
28.
29.
30.
31.
32.
33.
34.
35.	9,9
36.
37.
38.
39.
40.	91,3	-
41.	84.5
42.
43.
44.
45.
46.
47.
48.
49.	9,9
50.

ВАРИАНТ 7

№ п/п	Агрегат в работе %	Удельн. расход масел
1.		14,89
2.		4.54
3.		14,50
4.		14,50
5.		14,50
6.	2,5	14,50
7.	9,7	14,50
8.		14,50
9.		14,50
10.		14,50
11.	26,3	14,50
12.	7,6	10,1
13.	10.66	13,8
14.	6,1	14,5
15.		14,89
16.		4.54
17.		14,50
18.		14,50
19.		14,50
20.	2,5	14,50
21.	9,7	14,50
22.		14,50
23.		14,50
24.		14,50

25.	26,3	14,50
26.	7,6	10,1
27.	10.66	13,8
28.	6,1	14,5
29.		14,89
30.		4.54
31.		14,50
32.		14,50
33.		14,50
34.	2,5	14,50
35.	9,7	14,50
36.		14,50
37.		14,50
38.		14,50
39.	26,3	14,50
40.	7,6	10,1
41.	10.66	13,8
42.	6,1	14,5
43. 1		14,89
44. 2		4.54
45. 3		14,50
46. 4		14,50
47. 5		14,50
48. G	2,5	14,50
49. 7	9,7	14,50
50. 8		14,50

ВАРИАНТ 8

№ п/п	Агрегат в работе %	Кол-во вынужденных отказов
1.
2.
3.
4.
5.
6.	2,5
7.	9,7
8.
9.
10.
11.	26,3
12.	7,6	-
13.	10.66
14.	6,1
15.
16.
17.
18.
19.
20.	2,5
21.	9,7
22.
23.
24.

25.	26,3
26.	7,6	-
27.	10.66
28.	6,1
29.
30.
31.
32.
33.
34.	2,5
35.	9,7
36.
37.
38.
39.	26,3
40.	7,6	-
41.	10.66
42.	6,1
43.
44.
45.
46.
47.
48.	2,5
49.	9,7
50.

ВАРИАНТ 9

№ п/п	Агрегат в работе %	Удельн. расход масел
1.		14,89
2.		4.54
3.		14,50
4.		14,50
5.		14,50
6.	2,5	14,50
7.	9,7	14,50
8.		14,50
9.		14,50
10.		14,50
11.	26,3	14,50
12.	7,6	10,1
13.	10.66	13,8
14.	6,1	14,5
15.		14,89
16.		4.54
17.		14,50
18.		14,50
19.		14,50
20.	2,5	14,50
21.	9,7	14,50
22.		14,50
23.		14,50
24.		14,50

25.	26,3	14,50
26.	7,6	10,1
27.	10.66	13,8
28.	6,1	14,5
29.		14,89
30.		4.54
31.		14,50
32.		14,50
33.		14,50
34.	2,5	14,50
35.	9,7	14,50
36.		14,50
37.		14,50
38.		14,50
39.	26,3	14,50
40.	7,6	10,1
41.	10.66	13,8
42.	6,1	14,5
43.		14,89
44.		4.54
45.		14,50
46.		14,50
47.		14,50
48.	2,5	14,50
49.	9,7	14,50
50.		14,50

ВАРИАНТ 10

№ п/п	Агрегат в работе %	Коэф. использования
1.		0,948
2.		0,804
3.		0,564
4.		0,952
5.		0,347
6.	2,5	0,069
7.	9,7	0,115
8.		0,22
9.		0,54
10.		0,316
11.	26,3	0,356
12.	7,6	0,008
13.	10.66	0,12
14.	6,1	0,065
15.		0,948
16.		0,804
17.		0,564
18.		0,952
19.		0,347
20.	2,5	0,069
21.	9,7	0,115
22.		0,22
23.		0,54
24.		0,316

25.

26,3

0,356

⇐ Предыдущая 1 2 34

Поделиться с друзьями:

Дата добавления: 2016-12-31; Мы поможем в написании ваших работ!; просмотров: 405 | Нарушение авторских прав

Поиск на сайте:

Лучшие изречения:

Начинайте делать все, что вы можете сделать – и даже то, о чем можете хотя бы мечтать. В смелости гений, сила и магия. © Иоганн Вольфганг Гете
==> читать все изречения...

1518 -

| 1358 -