Задача 3. Построение уравнений регрессии

Построить уравнение линейной регрессии

Статистический анализ двумерных данных. Анализ двумерных данных включает в себя три основных цели: 1. Описание и понимание взаимосвязи. 2. Прогнозирование и предсказание нового наблюдения. 3. Корректировка и управление процессом. Существует два вида анализа двумерных данных, представленных переменными X и Y: Регрессионный анализ, определяет форму (вид) связи между этими переменными. Регрессионный анализ всегда проводится после корреляционного анализа, когда между переменными установлено наличие взаимосвязи. Регрессионный анализ используется для прогнозирования одной переменной на основании другой (как правило, Y на основании X), или показывает, как можно управлять одной переменной с помощью другой. Определение формы зависимости между переменными X и Y является одной из главных задач регрессионного анализа. Для этого необходимо построить уравнение регрессионной связи между Y и X (уравнение регрессии) следующего вида: Y = f (x) + e, где f (x) - функцией регрессии, e – величина, учитывающая случайные воздействия. Для выборочных данных уравнение регрессионной связи удобно представить следующим образом:

При наличии случайной составляющей e _i значения y_i имеют определенный разброс. Поэтому нет смысла подбирать функцию регрессии, проходящую через все точки. Основное правило подбора вида функции регрессии заключается в том, чтобы все точки диаграммы рассеяния были сконцентрированы около графика этой функции. На практике, поскольку мы располагаем выборочными данными, невозможно точно построить функцию регрессии, можно только получить ее оценку, которую обозначим как

. Уравнение, включающее оценку для функции регрессии, называется выборочным уравнением регрессии и имеет вид:

. Построив «выборочную» функцию регрессии далее необходимо проверить достоверность функции и ее параметров, а также провести оценку неизвестных значений (прогноз) зависимой переменной Y. Простейшей, с точки зрения анализа, является линейная взаимосвязь между X и Y, которая выражается в том, что точки на диаграмме рассеяния случайным образом группируются вдоль прямой линии, имеющей наклон (вверх или вниз). По выборке можно построить выборочную линейную функцию регрессии вида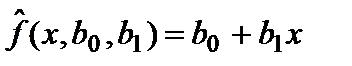

, которая является оценкой линейной функции регрессии f (x, b₀, b₁). Таким образом, выборочное уравнение линейной регрессии имеет вид:

. Коэффициенты b ₀, b ₁ являются оценками параметров b₀, b₁. Для вычисления коэффициентов b ₀, b ₁ используется метод наименьших квадратов (МНК), который характеризуется наименьшей суммой квадратов отклонений значений переменной Y от прямой. Это означает, что прямая на диаграмме рассеяния будет проходить «достаточно близко» к точкам (x_i, y_i). Коэффициент b ₁ определяет наклон прямой (его часто называют коэффициентом регрессии). При увеличении значения переменной X ровно на единицу значение переменной Y в среднем увеличивается (если b ₁>0) или уменьшается (если b ₁<0) на b ₁ единиц. Коэффициент b ₀ (постоянный член, или константа регрессии) определяет сдвиг прямой, т.е. такое значение Y, когда значение X равно нулю. При использовании МНК сдвиг определяется таким образом, чтобы прямая проходила через точку (

), где

– средние значения переменных X и Y соответственно. В тех случаях, когда нулевое значение X лишено смысла, сдвиг рассматривается как необходимая характеристика для построения функции регрессии и его не следует интерпретировать.

Подготовить набор исходных данных

При регрессионном анализе рассматриваются двумерные данные. В качестве исходных данных необходимо сформировать две последовательности величин с предположением наличия между ними взаимосвязи.

Построить график линейной зависимости между стоимостью и площадью жилого объекта

В Excel используются три метода построения функции линейной регрессии: команда Добавить линию тренда, инструмент анализа Регрессия и соответствующие статистические функции в Мастере функций. Инструмент анализа Регрессия помимо тех результатов, которые выдает команда Добавить линию тренда, позволяет получить дополнительную информацию о зависимости двух переменных.

Построить уравнение нелинейной регрессии

Анализируя диаграммы рассеяния двумерной совокупности данных, можно выявить три различных типа взаимосвязей между переменными X и Y. 1. Линейная взаимосвязь. 2. Отсутствие взаимосвязи. 3. Нелинейная взаимосвязь. Линейная взаимосвязь играет такую же важную роль для двумерных данных, как и нормальное распределение для одномерных данных. Прежде всего, линейную зависимость между переменными X и Y легче анализировать. На диаграмме рассеяния точки случайным образом могут концентрироваться вокруг прямой линии, или быть достаточно широко разбросаны, образуя некоторое облако. Набор данных линейной взаимосвязи не должен содержать сильных выбросов. Отсутствие взаимосвязи представляет собой особый случай линейной взаимосвязи, когда соответствующая диаграмма рассеяния имеет совершенно случайный характер, т. е. продвигаясь по ней слева направо, мы не обнаруживаем тенденции направленности вверх (увеличение) или вниз (уменьшение). Такая диаграмма имеет вид либо круглого, либо овального облака. Овал может иметь вертикальную или горизонтальную ориентацию, но без наклона. Фактически, если совокупность данных характеризуется отсутствием взаимосвязи, то, изменяя шкалу той или другой переменной, можно добиться того, что диаграмма рассеяния будет иметь круговую или овальную форму разброса точек. Нелинейная взаимосвязь характеризуется тем, что в двумерной совокупности данных точки на диаграмме рассеяния группируются вокруг некоторой кривой линии. Поскольку разновидностей кривых может быть чрезвычайно много, анализ нелинейной взаимосвязи существенно сложнее, чем линейной. Для переменных X и Y с нелинейной зависимостью корреляционный и регрессионный анализ следует использовать с осторожностью. В некоторых задачах бывает полезно преобразовать одну или обе переменные таким образом, чтобы получить между ними линейную взаимосвязь. Это позволяет упростить анализ (применив корреляцию и регрессию к линейной взаимосвязи), а полученные результаты, если удается, преобразовывают обратно в исходную форму. Важным шагом при выборе нелинейной формы зависимости является изучение графика. Ниже на рисунке изображены четыре выпуклые нелинейные кривые, которые могут быть получены на графике. Метка для каждой кривой обозначает направление выпуклости.

СЗ

СВ

ЮЗ

ЮВ

Направление выпуклости соответствует определенному виду функции регрессии.

Так, для данных, имеющих выпуклость в сторону северо-запада (СЗ), используются степенные (при x >1) и логарифмические функции; для данных, имеющих выпуклость в сторону юго-запада (ЮЗ), используются степенные, логарифмические или экспоненциальные функции; данным с выпуклостью в сторону юго-востока (ЮВ) соответствуют степенные (при x >1) и экспоненциальные функции.

Кроме того, все четыре кривые данных могут быть смоделированы квадратичной функцией (полиномом второй степени).

Если вид данных на графике не подходит к указанным выше примерам, то следует использовать какую-либо другую форму зависимости.

Например, если данные имеют две выпуклости (S -форма), то можно применить кубическую функцию (полином третьей степени).

В данной лабораторной работе рассмотрим четыре модели нелинейной зависимости между двумя переменными X и Y: полиномиальную, логарифмическую, степенную и экспоненциальную.

В качестве примера используем данные о ценах объектов недвижимости (см. лабораторную работу №5, таблицу 1).

Зависимой переменной Y является стоимость в тысячах долларов, а независимой переменной X – площадь в квадратных метрах.

Из проведенного в лабораторной работе №6 линейного регрессионного анализа для указанных данных получены график линейной функции регрессии и график остатков.

На графике остатков видно, что первые два объекта недвижимости с небольшой площадью и последние несколько объектов с большой площадью имеют отрицательныеостатки.

Это наблюдение показывает, что нелинейное приближение может дать лучшие результаты.

При внимательном рассмотрении диаграммы рассеяния (см. лабораторную работу №5, задание 1) можно заметить, что график функции регрессии имеет небольшую выпуклость в сторону СЗ, хотя кривизна небольшая.

Следовательно, для анализа можно использовать квадратичную, степенную или логарифмическую функции.