Задача №1
Построить изображение пирамиды в основании которой лежит равнобедренный треугольник.
Решение:
Здесь и в дальнейшем строить изображение пирамиды будем согласно приведенному алгоритму.
1. 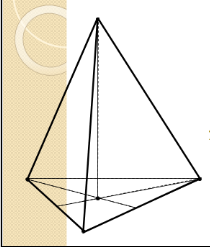 Строим основание пирамиды. Равнобедренный треугольник изображается произвольным треугольником.
Строим основание пирамиды. Равнобедренный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам. Одним из таких перпендикуляров будет медиана, проведенная к основанию треугольника. На проекционном чертеже основание высоты занимает произвольное местоположение на проведенной медиане.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Задача №2
Построить изображение пирамиды в основании которой лежит прямоугольный треугольник.
Решение:
1. 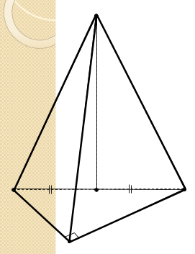 Строим основание пирамиды. Прямоугольный треугольник изображается произвольным треугольником.
Строим основание пирамиды. Прямоугольный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам. В основании прямоугольный треугольник, поэтому основание высоты – середина гипотенузы.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Задача №3
Построить изображение пирамиды в основании которой лежит правильный треугольник.
Решение:
1. 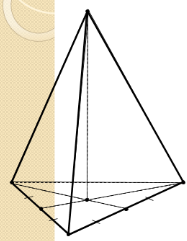 Строим основание пирамиды. Правильный треугольник изображается произвольным треугольником.
Строим основание пирамиды. Правильный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды. По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам. В основании правильный треугольник, поэтому основание высоты – точка пересечения его медиан.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
 Задача №4
Задача №4
Построить изображение пирамиды в основании которой лежит прямоугольник.
Решение:
1. Строим основание пирамиды. Прямоугольник изображается произвольным параллелограммом.
2. Строим высоту пирамиды. По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам. В основании прямоугольник, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Задача №5
Построить изображение пирамиды в основании которой лежит квадрат.
Решение:
1. 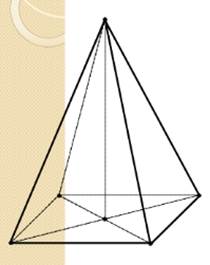 Строим основание пирамиды. Квадрат изображается произвольным параллелограммом.
Строим основание пирамиды. Квадрат изображается произвольным параллелограммом.
2. Строим высоту пирамиды. По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам. В основании квадрат, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Задача №6
Построить изображение пирамиды в основании которой лежит равнобедренная трапеция.
Решение:
1.  Строим основание пирамиды. Трапеция изображается трапецией.
Строим основание пирамиды. Трапеция изображается трапецией.
2. Строим высоту пирамиды. По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам. В основании равнобедренная трапеция, поэтому основание высоты занимает произвольное местоположение на отрезке соединяющем середины оснований.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.






