Определение 2.3.1. Пусть 
.
1) Группа 
называется - группой, если 
.
2) Группа называется 
- группой, если 
.
3) Группа называется -группой, если 
.
Замечание 2.3.1. Пусть 
.
1) Число 
называется -числом, если 
.
2) Число называется -числом, если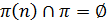 
.
3) Число называется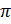 
d-числом, если 
,
где 
.
Замечание 2.3.2. Если =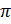 
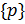, то - группа( - группа,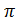 
d- группа) называется 
-группой (соответственно 
-группой, 
d-группой).
Замечание 2.3.3. Если 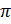= 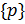, то - число( - число, 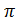d- число) называется -числом (соответственно -числом, d-числом).
Определение 2.3.2. Подгруппа 
группы называется холловской -подгруппой, если 
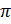— -число, 
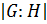— -число. Обозначается 
.
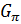Теорема 2.3.1 (Холла). Пусть — конечная разрешимая группа, 
. Тогда:
1) В существуют холловские -подгруппы.
2) Всякая -подгруппа группы содержится в некоторой холловской 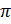-подгруппе группы .
3) Любые две холловские -подгруппы группы сопряжены в .
Определение 2.3.3. Конечная группа называется -разрешимой, где , если всякий главный фактор группы является либо -группой, либо абелевой -группой для некоторого 
.
2. Если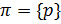 
, то -разрешимая группа, называется -разрешимой.
Теорема 2.3.2. Пусть .
1) Всякая подгруппа и факторгруппа -разрешимой группы является 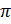-разрешимой.
2) Если 
и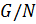 
-разрешимы, то 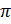-разрешима.
3) Если -разрешима и 
, то 
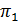-разрешима.
Следствие 2.3.1. Пусть 
.
1) Всякая подгруппа и факторгруппа -разрешимой группы является -разрешимой.
2) Если и 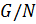-разрешимы, то -разрешима.
Теорема 2.3.3 (Чунихина). Пусть — конечная -разрешимая группа, . Тогда:
1) В существуют холловские -подгруппы и холловские -подгруппы.
2) Всякая -подгруппа группы содержится в некоторой холловской 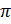-подгруппе группы ; всякая -подгруппа группы содержится в некоторой холловской -подгруппе группы .
3) Любые две холловские -подгруппы ( -подгруппы) группы сопряжены в .
Следствие 2.3.2. Пусть — конечная -разрешимая группа, . Тогда:
1) В существуют силовская -подгруппы и холловские -подгруппы.
2) Всякая -подгруппа группы содержится в некоторой силовских -подгруппе группы ; всякая -подгруппа группы содержится в некоторой холловские -подгруппе группы .
3) Любые две силовские -подгруппы (холловские -подгруппы) группы сопряжены в .
-свойства конечных групп:
1. Говорят, что группа обладает 
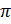-свойством, если в существуют холловские -подгруппы. Группа называется -группой, если обладает -свойством. Теоремы о существовании в группе холловских -подгрупп называются -теоремами.
2. Говорят, что группа обладает 
-свойством, если обладает -свойством и любые две холловские 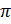-подгруппы группы сопряжены в . Группа называется -группой, если обладает -свойством. Теоремы о том, что любые две холловские -подгруппы группы сопряжены в , называются -теоремами.
3. Говорят, что группа обладает 
-свойством, если обладает -свойством и всякая 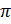-подгруппа группы содержится в некоторой холловской 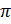-подгруппе группы . Группа называется -группой, если обладает -свойством. Теоремы о том, что всякая -подгруппа группы содержится в некоторой холловской 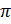-подгруппе группы , называются -теоремами.
Заключение
В реферате были выполнены следующие задачи:
1. Рассмотрены определения разрешимой группы, -группы, -группы, 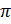d- группы, холловские 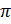-подгруппы, 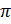- разрешимой группы и другие.
2. Изучены основные свойства разрешимых групп.
3. Исследованы критерии разрешимости конечных групп.
4. Изучены -разрешимые и -разрешимые группы.
5. Рассмотрены -свойства конечных групп.
Список литературы
1. Воробьев Н.Н. Алгебра классов конечных групп. Витебск: ВГУ имени П.М. Машерова, 2012.
2. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982.
3. Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры. - М.: Физико-математическая литература, 2000.
4. Кострикин А.И. Введение в алгебру. Часть 2. Линейная алгебра. - М.: Физико-математическая литература, 2000.
5. Кострикин А.И. Введение в алгебру. Часть 3. Основные структуры алгебры. - М.: Физико-математическая литература, 2000.
6. Курош А.Г. Теория групп. – М.: Физико-математическая литература, 2011.
7. Монахов В.С. Введение в теорию конечных групп и их классов: учебное пособие. – Мн.: Вышэйшая школа, 2006.
