Одной из задач начертательной геометрии является изображение пространственных форм на плоскости, которые должны быть удобоизмеряемыми, чтобы по ним можно было воспроизвести объект в натуре, и наглядными. Ортогональные проекции обладают сравнительно плохой наглядностью вследствие того, что на каждой проекции отсутствует одно измерение – например на фасаде отсутствует глубина. Тени, построенные на фасаде, позволяют лучше представить взаимное положение элементов, глубину ниш, величину выступов. По построенным теням можно получить общее представление о композиции фасада. Поэтому рассмотрим примеры, используя те же приемы, что и при построении теней геометрических тел.
Тени в нишах
Ниши это углубление в стене. Если задняя грань ниши параллельна фронтальной плоскости проекций, ниши называют плоскими
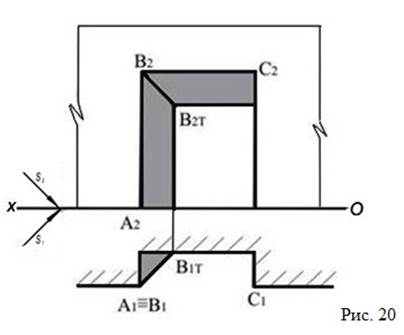
Тень, падающая от фронтального обрамления ниши, повторит его форму на задней грани (см. рис. 20).
Построение проекций собственной и падающей теней прямоугольной ниши нужно строить от ребер АВ и ВС. От вертикального ребра АВ (проекции А1В1, А2В2)тень падает на горизонтальную плоскость П1 и на фронтальную плоскость задней стенки ниши.
От горизонтальной прямой ВС (В1С1, В2С2) тень падает частично на заднюю фронтальную стенку ниши в виде прямой, параллельной ребру ВС, и частично на правую боковую грань ниши, где она параллельна профильной проекции луча света, так как ребро ВС занимает профильно – проецирующее положение.
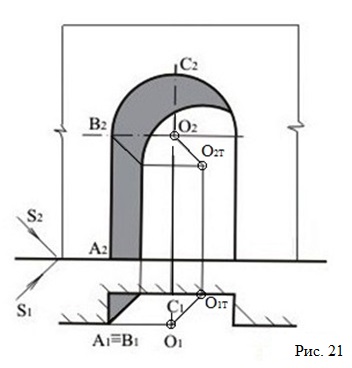
На рис. 21 показано построение тени в нише, перекрытой полуциркульной аркой.
Для построения тени в нише необходимо построить тень от прямой АВ и от дуги окружности, проходящей через точки В и С. Тень от дуги окружности будет окружность того же радиуса с центром в точке От.
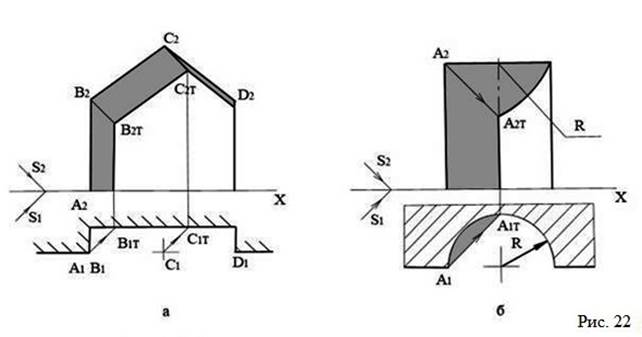
На рис. 22 показаны другие формы ниш, но построение теней выполняется аналогично построению теней в прямоугольной нише. Здесь тени от отрезков АВ, ВС, СД параллельны самим отрезкам.
В цилиндрической нише (см. рис.22б) падающая тень ограничена прямой линией, делящей нишу пополам, и четвертью окружности.
Падающие тени от выступающих частей здания.
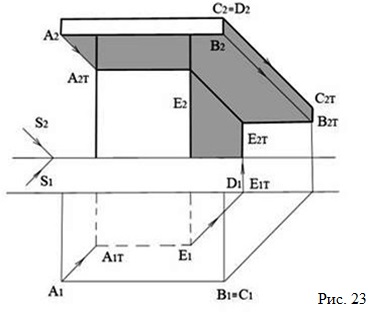Тень от карниза падает от прямых АВ, ВС и СД (см. рис. 23). Тень от прямой АВ будет параллельна самой прямой, так как прямая параллельна той плоскости, на которую падает тень. Тень от прямой ВС ложится на фронтальную плоскость параллельно самой прямой, а тень от прямой СД, как от прямой, перпендикулярной фронтальной плоскости, пройдет по направлению светового луча. Ребро Е дает параллельную тень на фронтальной плоскости проекций.
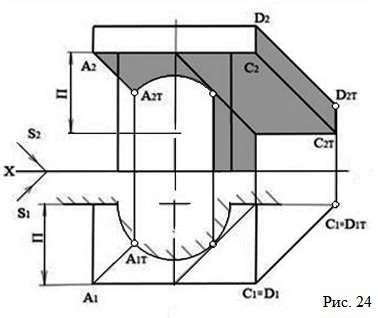Построение тени от полуколонны на стене и от абака на колонну и стену, показано на рис. 24, а также построена собственная тень полуколонны, имеющей форму полуцилиндра. Через тень точки С на стене проходит три линии, поэтому строятся три тени. Тень от СД вертикальна, тень от АС горизонтальна, тень от прямой, проходящей через точку С перпендикулярно к стене, параллельна фронтальной проекции луча света и расположена внутри тени от абака.
Тень, падающая от колонны, проходит по собственной тени колонны. Эта тень будет вертикальна, так как вертикальна граница собственной тени.
Через точку А также проходит три линии. Тень от вертикальной прямой не нужна, так как эта прямая не принадлежит границе собственной тени абака. Тень от прямой АС – в натуре дуга эллипса – проецируется на плоскость П2 в дугу окружности. Тень от АВ параллельна фронтальной проекции светового луча.
На рис. 25 показано построение теней от абака, имеющего форму полуцилиндра. В этом случае нужно взять на нижнем основании цилиндра некоторое количество точек и, проведя через них лучи света, определить тени точек на поверхности колонны.
Точка С найдена на пересечении границы собственной тени колонны с границей тени, падающей от абака на колонну. Она построена методом обратных лучей - через точку С2т* проведен обратный луч до пересечения с границей собственной тени в точке С2т.
Так же с помощью обратного луча построена точка А2т*, в которой граница падающей тени пересекается с левой контурной образующей колонны; вначале построена точка А1, затем найдена точка А2. Через точку А2 проведена фронтальная проекция луча света, которая пересекается с фронтальной проекцией образующей в точке А2т*.
Граница тени, падающей от абака на стену, представляет собой две дуги эллипсов и отрезок прямой, касательной к ним.
Продольное вспомогательное проецирование на осевую световую плоскость используется и при построении тени на сложные продольные формы. На рис. 41 показаны стена, цоколь и конус, от которого следует построить тень на вертикальную стену и цоколь здания.
Световая плоскость, проходящая через ось конуса, пересекает стену и цоколь здания по линии, зеркально симметричной этому профилю. Эту линию строят с помощью расстояния m от оси конуса до основной плоскости стены. Тень Sт² от вершины конуса падает на построенную линию пересечения, так как вершина лежит в плоскости α. Дальнейшее построение тени показано при определении точек тени 1т² и 2т² на одной из продольных прямых. Берут точку А на пересечении этой продольной прямой с линией пересечения световой плоскости α, проводят обратный луч света до пересечения с контуром собственной тени конуса в точках 1′2 и 3′2.
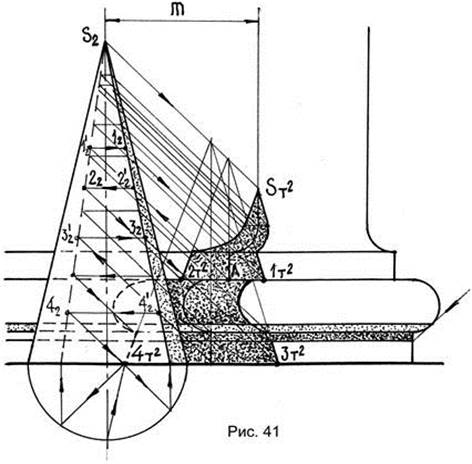Определяют симметричные им точки 12 и 22, через которые проводят лучи света до пересечения с той же продольной прямой, где и определяют 1т² и 2т². Тени на других характерных продольных формах строят в той же последовательности.
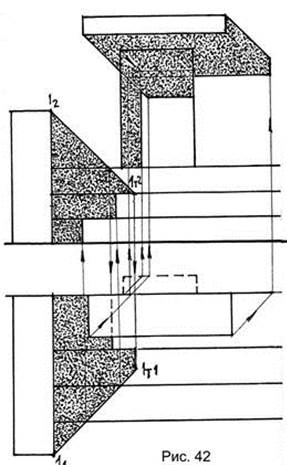На рис. 42 показано построения теней от барьеров на ступеньки и от козырьков на стены здания.
На рис. 50 показано построение тени от вазы на фронтальную стену. Сначала построены собственные тени на каждом элементе вазы и падающие от них на поверхности вазы, а затем – падающая на стену от границ полученных собственных теней.
Для определения контура падающей на стену тени строятся последовательно тени от всех зафиксированных горизонтальных окружностей вазы на плоскость, отстоящую от оси вазы на расстояние m. Проводятся огибающие кривые к построенным теням от горизонтальных окружностей вазы, которые и являются очерком падающей тени от вазы на фронтальную плоскость.
Выполнение задания можно разделить на четыре этапа.
1. Вычертить контур вазы, используя при этом построения архитектурных обломов (рис. 53-55). Задать расстояние m от оси вазы до фронтальной плоскости, на которую упадет тень от вазы.
2. 
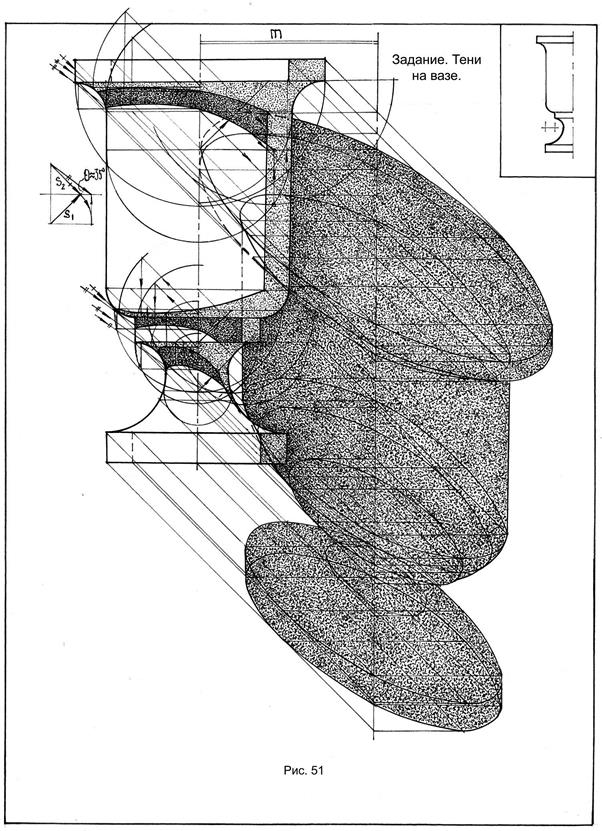
Построить собственные тени на вазе. Для этого необходимо уточнить, из каких поверхностей вращения состоит ваза, какие архитектурные обломы использованы при её конструировании. Например, на вазе, изображенной на рис. 51 и 56 (примеры выполнения задания), использованы такие элементы, как цилиндрические – в верхней, средней и нижней частях, архитектурные обломы – прямая выкружка, прямой четвертной вал, скоция. Таким образом, на цилиндрах, или в тех сечениях, где можно провести касательные цили-ндрические поверхности, собственные тени строятся, как показано на рис. 21. На выкружке и четвертном валу точки 1, 2, 3, 4, принадлежащие линии контура собственной тени, построены как на рис. 30, а на скоции точки 5, 6, 7, 8, и 9 построены, как показано на рис. 28.
3. Далее следуют построе-ния падающих теней. Для построения падающей тени от горизонтальной окружности на тело вращения используют способ вписанных световых квадратов
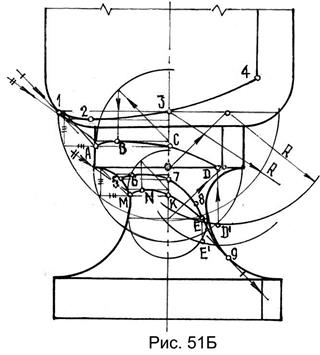
(рис. 46). Точки А и С (рис. 51, А) построены с помощью вписанного светового квадрата в основание цилиндрической плиты, который касается контура вазы. Так определяются точка А и в этом же сечении точка С на оси. Наивысшая точка В строится с помощью луча, проведенного под углом 35° из крайней точки горизонтальной окружности до пересечения с контуром вазы. Определяется сечение, которое делится в отношении 3:7 (рис. 21). Таким же образом построена точка N (рис. 51Б). Для построения точки D (рис. 51, А) выбрано произвольное сечение на вазе и повернуто во фронтальное положение. Далее центр сечения О проецируется под 45° в положение О′, из которого радиусом R проводим окружность. В пересечении двух окружностей определяется точка D′ и проецируется на исходное сечение I. Так построена точка D. Таким же образом построена точка Е (рис. 51Б). Кривые линии АВСD и MNKE – контуры падающей тени на вазе.
4. Для определения контура падающей тени от вазы на стену строятся последовательно тени от всех зафиксированных горизонтальных окружностей вазы. Очерком падающей тени будут линии, огибающие падающие тени от выбранных окружностей. На рис. 56 приведен еще один пример выполнения задания «Тени на телах вращения типа вазы в прямоугольных проекциях».
Задание выполняется на чертежной бумаге формата А3 в карандаше с последующей отмывкой китайской тушью или акварельными красками.
Интересным является способ построения теней на симметричных архитектурных формах с использованием вспомогательного проецирования на осевые плоскости.
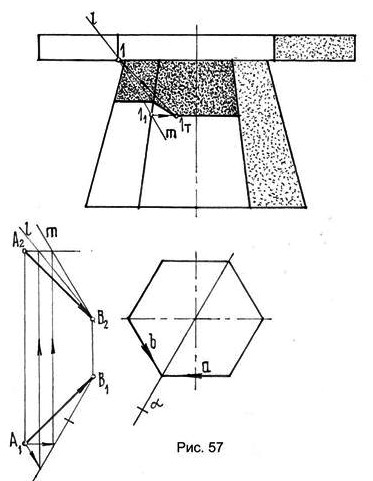На рис.57 показано применение этого приема при построении падающей тени от шестиугольной плиты на такую же в плане пирамиду.
Для построения падающей тени от точки I луч света АВ проецируется в направлении а на осевую плоскость α, в которой лежит точка I и левое среднее ребро пирамиды, параллельно горизонтальным прямым передней грани пирамиды. Фронтальной проекцией луча света при этом является отрезок m. Далее из точки I - фронтальной проекции изображения проводят луч, параллельный m, до пересечения с ребром пирамиды в точке I1.Затем проводят горизонтальную прямую, которая в пересечении с лучом света, проходящим через точку I, образует искомую тень IТ. Вправо от нее тень от продольной прямой, проводят на параллельную ей плоскость параллельную самой прямой.
Для определения падающей тени на левой грани луч света проецируется на ту же осевую плоскость в направлении b. Получено направление l, параллельная которому прямая, проведенная через точку I, пересекаясь с тем же ребром пирамиды, определит уровень падающей тени на первую грань пирамиды.
На рис.58 этот прием использован при построении тени довольно сложной формы, образованной пересечением горизонтальных цилиндров с одинаковыми направляющими. Для определения теней правой цилиндрической поверхности луч света АВ проецируется на фронтальную осевую плоскость параллельно образующей этой же поверхности. Проекцией луча света служит вертикальная прямая А3В2. Тогда вертикальная касательная к контуру поверхности определит границу собственной ее тени. Построение падающей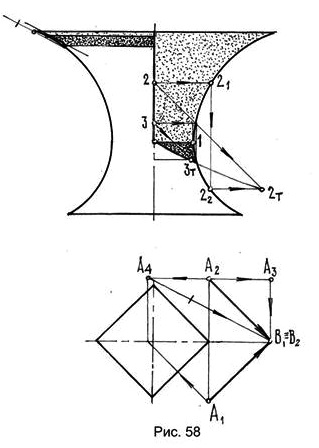 
тени показано при построении тени от точки 2. Для этого луч света проецируется на осевую фронтальную плоскость в направлении образующих, после чего получают проекцию 21 точки 2. Через точку 21 проводят вертикальную линию, пересекающую контур в точке 22. Пересечение луча света, проведенного через точку 2, с горизонтальной прямой, проходящей через точку 22, определяет искомую тень 2т. Поскольку тенью будет кривая линия, для уточнения ее формы необходимо построить таким же образом еще несколько точек тени.
Для определения теней на левой цилиндрической поверхности, луч света проецируется на ту же осевую плоскость в направлении образующих этой поверхности. Получают проекцию А4В2. Касательная к контуру, параллельная А4В2, определяет уровень собственной тени, секущая из крайней контурной точки – падающую тень.
На рис. 59 показано построение собственных и падающих теней на куполе. Купол составлен из пересекающихся горизонтальных цилиндрических поверхностей. Для построения собственных теней на левой и правой поверхностях использовано вспомогательное проецирование на осевую фронтальную плоскость β луча света АВ. Тогда касательная, параллельная А3В2, определит границу собственной тени на правой поверхности, а касательная, параллельная А4В2, – такую же тень на левой поверхности. Для определения собственной тени на средней поверхности использовано продольное проецирование на осевую плоскость α. Вспомогательная проекция С3D2 луча света СD определяет направление касательной к кривой пересечения, лежащей в той же плоскости α, для построения границы собственной тени.
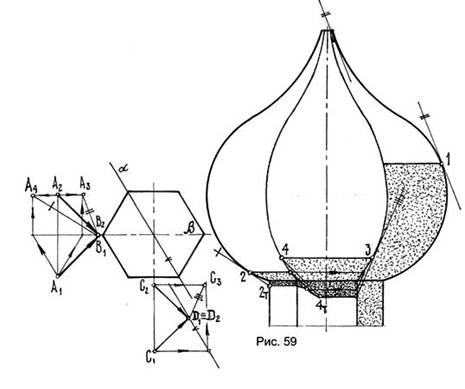Та же касательная, пересекаясь с ребром призмы, определит падающую тень на средней грани, а ранее проведенная касательная, параллельная А4В2 в пересечении с крайним ребром призмы, определит падающую тень на левой грани призмы.
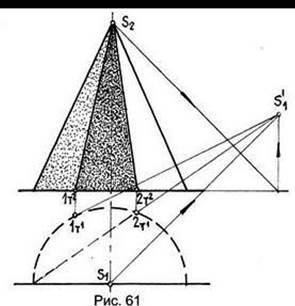На рис. 60 изображена цилиндрическая закрытая ниша. Падающая тень образуется от продольной и вертикальной прямых обрамления. Тень от продольной прямой зеркально повторяет план ниши и поэтому будет полуокружностью с центром, лежащим на оси цилиндра. Луч света из крайней левой точки 12 этой прямой, ограничит полуокружность 11. Она зафиксирует вертикальную прямую тени от вертикальной прямой обрамления. Собственная тень ниши образуется так же, как на поверхности цилиндра, только невидимая его образующая становится видимой.
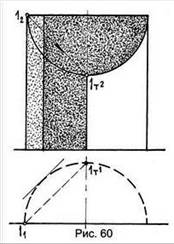
На рис. 61 показано построение тени в вертикальной конической нише. На рис. 66 построена тень, падающая от пирамиды на поверхность цилиндрической ниши, расположенной с ней на одной оси. При этом использовано продольное вспомогательное проецирование на световую плоскость, линией пересечения которой с поверхностью ниши является прямая Sт21. Тень от вершины S падает на эту линию пересечения, поскольку вершина лежит в осевой плоскости. Затем, чтобы построить падающую тень от точки I(I2) пирамиды, с помощью продольной прямой найдена симметричная её точка I′2 и через неё проведен луч света до пересечения с поверхностью в точке I0. Из центра О, лежащего на оси пирамиды, проведена полуокружность – пересечение поверхности ниши со световой плоскостью, проходящей через продольную прямую I2I′2. Полуокружность можно назвать тенью от продольной прямой на поверхность ниши, повторяющей зеркально план ниши. Так же построена тень 2т² от точки 2 на другом ребре, бросающем тень, и можно найти еще сколько угодно точек падающей тени.
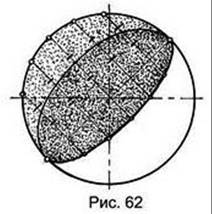На рис. 62 показано построение сферической ниши, которая образуется половиной поверхности сферы. Собственная тень ниши построена так же, как на рис. 32, где на сфере она была невидимой. Контур падающей тени строят путем деления полухорд, расположенных под углом 45° к горизонтальному направлению, на три равные части и откладывания одной трети на их продолжениях. В практике встречаются ниши с глубинной осью.
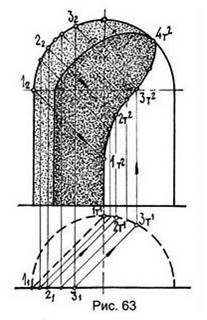
Тень в цилиндрической нише со сферическим завершением изображена на рис. 63.
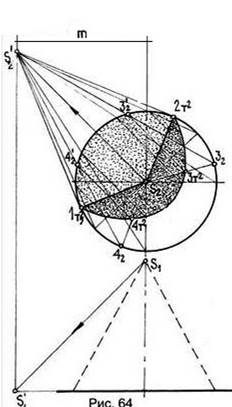
На рис. 64 показано построение теней в конической нише, глубинная ось которой равна m. Вершина конуса проецируется на основание в направлении, параллельном лучам света, в результате чего получают точку S′2. Касательные прямые к окружности основания, проведенные через точку S′2, определяют образующие собственной тени конуса. Построение точек падающей тени можно проследить при определении точки 3т². Для этого строят вспомогательную проекцию S′232 произвольно взятой образующей S3 конуса. Точка пересечения 3′2 перенесена лучом света на ту же образующую S232. Так можно построить сколько угодно точек падающей тени.
Построение тени в плоской шестигранной нише с глубиной m показано на рис. 65.
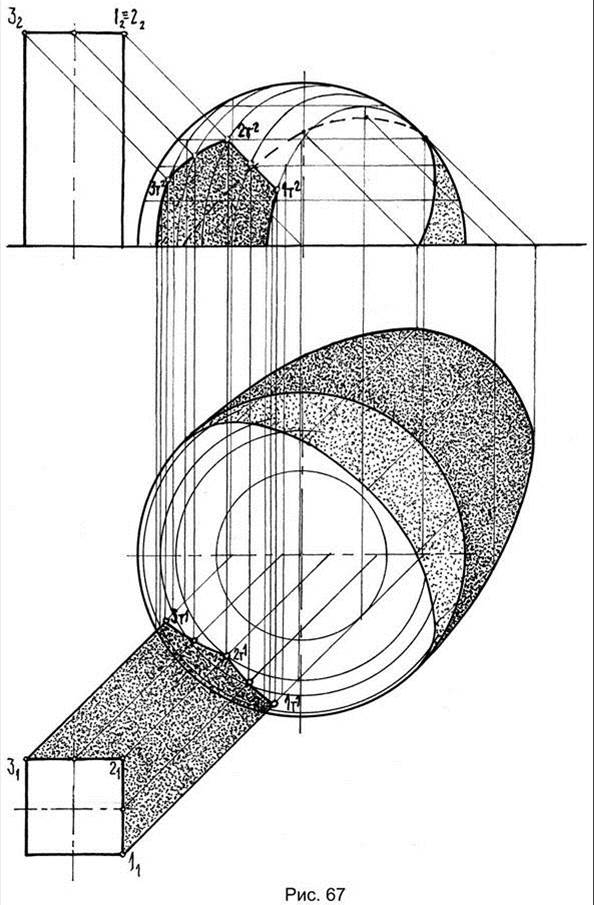
Если тени падают на сложные поверхности (при различном сечении поверхностей, отбрасывающих тень), а применить описанные приемы нельзя, то используются способы секущих плоскостей и обратных лучей. Секущие плоскости, как правило, используются проецирующие, и тени при этом строятся с использованием двух проекций.
На рис. 67 через вертикальные ребра призмы проведены вертикальные световые плоскости, определены линии пересечения и с поверхностью сферы. Последние ограничены световыми лучами из граничных точек тех же ребер. Промежуточные точки теней от горизонтальных ребер найдены с использованием дополнительных секущих плоскостей.
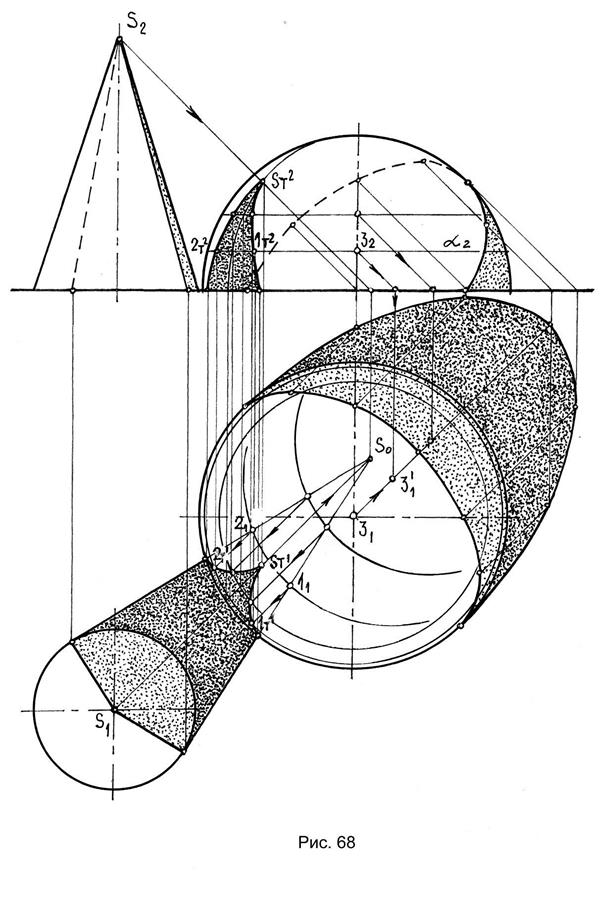
На рис. 68 тени отбрасывают наклонные образующие конуса, поэтому для построения линий пересечения проще использовать способ обратных световых лучей. Для этого строят падающую тень от конуса на горизонтальную плоскость его основания. На ту же плоскость в направлении света проецируют произвольное сечение α. Точки пересечения полученных теней 11 и 21 спроецированы затем в направлении, обратном световым лучам, на сечение α, где и получены точки тени 1т¹ и 2т¹.световым лучам, на сечение α, где и получены точки тени 1т¹ и 2т¹.
