ТЕНИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ
При построении теней в ортогональных проекциях направление лучей света принимают параллельным диагонали куба, грани которого параллельны плоскостям проекций (рис. 1). Все три проекции диагонали наклонены к осям проекций под углом 45º.
Падающие тени от точки, прямой и плоской фигуры. Способ следа луча.
Чертёж любого сооружения состоит из отрезков прямых или кривых линий, которые в совокупности могут представлять различные геометрические формы.
Тень от точки на какую-либо поверхность (см. рис. 2) является точкой пересечения с этой поверхностью луча света, проведённого через данную точку. От точки, расположенной в пространстве тень может падать или на пл. π1 или π2. На рис.2 показано построение тени точек А и В на эпюре. Из двух теней Ат и Ату, Вт и Вту, первые - Ат и Вт будут реальными и действительными, вторые - Ату и Вту будут мнимыми.
Тень от прямой линии на поверхность - это есть линия пересечения лучевой плоскости с этой поверхностью. Плоскость, проходящая через заданную прямую линию параллельно световому лучу называется лучевой плоскостью. Тень от прямой линии может быть точкой, прямой, ломаной или кривой.
Построение тени отрезка прямой на две плоскости проекций ведется в следующей последовательности:
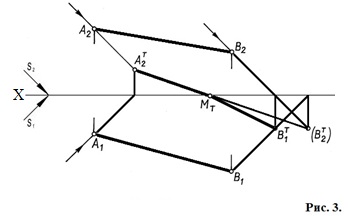
1. Тень отрезка на одну из плоскостей строят, предполагая, что второй не существует. В примере на рис. 3 сначала построена тень отрезка на фронтальную плоскость проекций.
2. Если построенная тень пересекает ось проекций, то в этой точке тень преломляется и с одной плоскости проекций переходит на другую. В эту точку и будет направлена преломившаяся тень отрезка прямой. На рис. 3 такой точкой является реальная тень точки В на горизонтальной плоскости проекций.
Закономерности расположения теней отрезков прямых частного положения:
· Если отрезок прямой параллелен плоскости, то тень от него на эту плоскость параллельна отрезку и равна ему по величине.
· Если прямая перпендикулярна к плоскости, то тень, падающая от неё на эту плоскость, совпадает с проекцией светового луча на этой плоскости.
· Если прямая параллельна направлению светового луча, то тень от неё – точка.
· Параллельные прямые имеют параллельные тени.
Тень плоских фигур
Построение теней плоской фигуры упрощается в тех случаях (см. рис. 4), когда точка или принадлежащая ей прямая, расположена в плоскости проекций, потому, что точки B и C или прямая BC совпадают со своей тенью.
Тень четырехугольника, занимающего общее положение.
Чтобы построить падающую тень плоской фигуры четырехугольника ABCD, занимающего общее положение (см. рис. 5), когда его вершины и стороны не принадлежат плоскостям проекций, нужно найти тени от каждой его вершины, соединив между собой прямыми линиями одноименные тени точек.
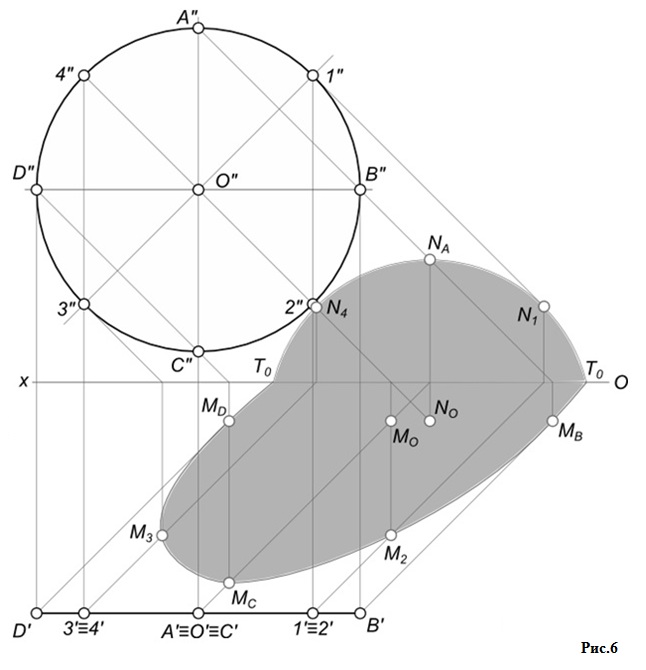
При построении тени круга, расположенного параллельно фронтальной плоскости проекций (см. рис. 6), разделяем круг на 8 равных частей и находим тени всех этих точек, которые соединяем плавной кривой. На фронтальной плоскости проекций достаточно найти тень от центра круга, которая послужит центром для проведения окружности, служащей контуром падающей тени от круга.
Тени геометрических тел
Построение тени прямого параллелепипеда, стоящего на горизонтальной плоскости проекций (см. рис. 7).
Построение тени прямого кругового цилиндра, стоящего на горизонтальной плоскости проекции.
Чтобы построить контур собственной тени поверхности цилиндра (см. рис. 8), необходимо провести к этой поверхности касательные лучевые плоскости, параллельные направлению лучей света, и найти линии касания (образующие цилиндра). Вдоль этих образующих пройдет контур собственной тени.
Контур падающей тени от цилиндра состоит из падающих теней от образующих 2 и 4 и падающей тени от полуокружности DAB.
Построение тени прямого кругового конуса, стоящего на горизонтальной плоскости проекций.
В данном случае (см. рис. 9), тень основания конуса совпадает с ним, остается найти тени только от вершины конуса, которые падают на фронтальную плоскость проекции в точку NS и горизонтальную плоскость проекции в точку MS. Из точки MS проводим прямые касательные окружности основания и находим на ней точки A`≡MA и B`≡MB, соединив которые с вершиной конуса S`, получим падающую тень конуса на горизонтальной плоскости проекций.
Падающую тень конуса на фронтальную плоскость проекции получим, соединив точки преломления T0 и NS.
Тени от шара в ортогональных проекциях строят исходя из представления, что шар в лучах света формирует цилиндр, пересечение образующих которого с плоскостями проекций дает их линии пересечения или границы тени, основываясь на этом представлении, выполняем следующее (см. рис. 10):
· через центр шара O проводим луч света и находим его следы MO и NO на плоскостях проекций;
· через центр шара O, перпендикулярно световым лучам, проводим плоскость β, задав ее следами;
· находим линию пересечения поверхности шара с плоскостью β, которая определяет границы собственной тени шара α, применяя для этого перемену плоскости проекции;
· отмечаем на горизонтальной плоскости проекции G` и проведя через точку G вспомогательную горизонтально проецирующую плоскость δΗ находим ее недостающую проекцию G", применяя при этом конкурирующие точки и определение видимости;
· проводим лучи света через центр шара O и точку G находим их следы MO и MG на горизонтальной плоскости проекции, определяющие большую полуось эллипса;
· проводим луч света через точку F, находим ее след на горизонтальной плоскости проекции MF. Отрезок MO MF определяет малую полуось эллипса; выполняем построение эллипса до точек перелома тени;
· аналогично выполняем построение падающей тени от шара на фронтальную плоскость проекции.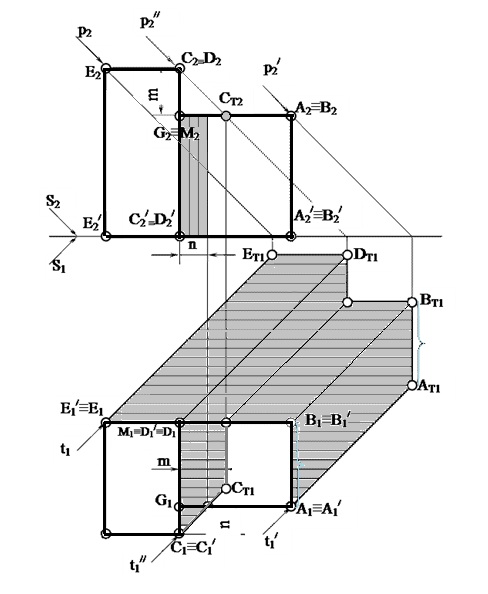 
Построение теней разновысотных объектов
Построение теней лестничного марша
