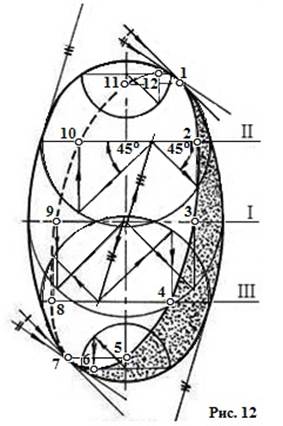
Собственные тени сферы можно построить специальным способом (см. рис. 11), задав двенадцать характерных точек для проекции окружности – контура собственной тени сферы. Поясное сечение сферы, принадлежащее описанному цилиндру, делится в соотношении 3/7 в обе стороны от центра (точки 3 и 9). В сечении, где касательная – образующая обертывающего конуса – наклонена под углом 45°, определяются точки – на контуре сферы и 11 – на ее оси.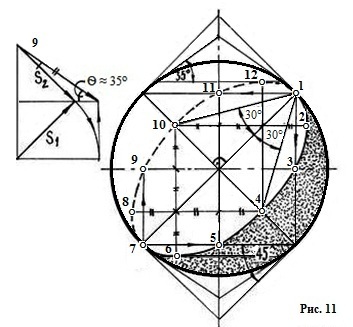 
Точки находятся следующим образом: Если надеть на сферу конус, с вершиной, обращенной вниз, то найдем точки 5 и 7. В сечении, где можно провести касательный конус к сфере с образующими, наклоненными к основанию этого конуса под углом θ≈350, определяется точка 12, делящая радиус в отношении 3/7, если касательный конус располагается вершиной вверх; и точка 6, если конус – располагается вершиной вниз, точка 12 называется – наивысшей, а точка 6 - наинизшей.
Для построения точек 4 и 10 необходимо из точки 1 провести прямые, под углом 30° по отношению к прямой 1-7, до прямой, проходящей под прямым углом к прямой 1-7. Точки 2 и 8 строятся путем отложения трех горизонтальных одинаковых отрезков, для точки 2 точка 10, а для точки 8 точка 4.
При построении эллипсоида вращения (рис. 12), использован прием «обертывающего вертикального цилиндра», который «надевается» на поясное сечение эллипсоида. Далее делим радиус в обе стороны от центра в отношении 3/7 и получаем точки 3 и 9. Точки тени на контуре и на оси 1, 11 и 5, 7 получаются путем проведения касательных конусов с образующими под 45° к основанию. Для построения наивысшей точки 12 и наинизшей – 6 проведены касательные конусы θ≈350, с вершинами, обращенными вверх и вниз, соответственно, радиус сечения делится в отношении 3/7. В произвольно выбранных сечениях II и III проведены обертывающие конусы и выполнены необходимые построения. Так построены точки собственной тени на эллипсоиде: 2, 10 в сечении II и 4,8 в сечении III.
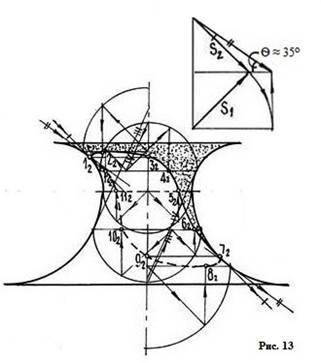На рис. 13 показаны построения точек контура собственной тени на поверхности вращения одного из архитектурных обломов, образующая которого есть кривая – скоция,. Поясное сечение поверхности вращения, которое принадлежит описанному цилиндру, делится в отношении 3/7. Получаем точки 5 и 11. На контуре поверхности и на оси построены точки 1,3 и 7,9 в результате построения обертывающих конусов (вершиной – вверх и вершиной - вниз) с образующими под углом 45°. Точки 2 и 8, наивысшая и наинизшая, строятся с помощью описанных конусов с образующими под углом θ≈35° и делением радиусов в отношении 3/7.
Построения собственной тени на поверхности тора
Последовательность построения точек контура собственной тени на торе (см. рис. 14), следующая:
1. Строятся точки в поясном сечении, где описывают цилиндр, и радиусы делятся в отношении 3/7. Это точки 3 и 9.
2. Определяются точки на контуре поверхности и на оси 1,11 и 5,7. Для этого проводятся лучи, касательные к контуру, параллельные лучу S2.
3. Проводится луч под θ≈35°, касательный к контуру поверхности, радиус в этом сечении делится в отношении 3/7. Определяются наивысшая точка 12 и наинизшая 6.
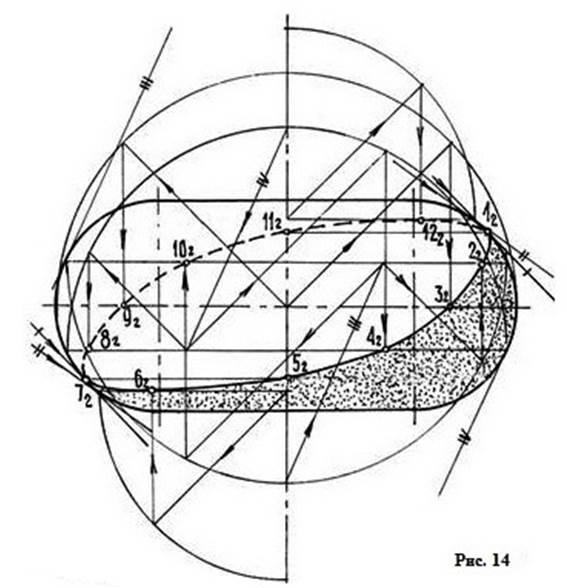4. Для построения дополнительных точек выбираются произвольные сечения на поверхности, описываются конусы с вершинами, направленными вверх и вниз, и строятся точки 2,10 и 4,8.
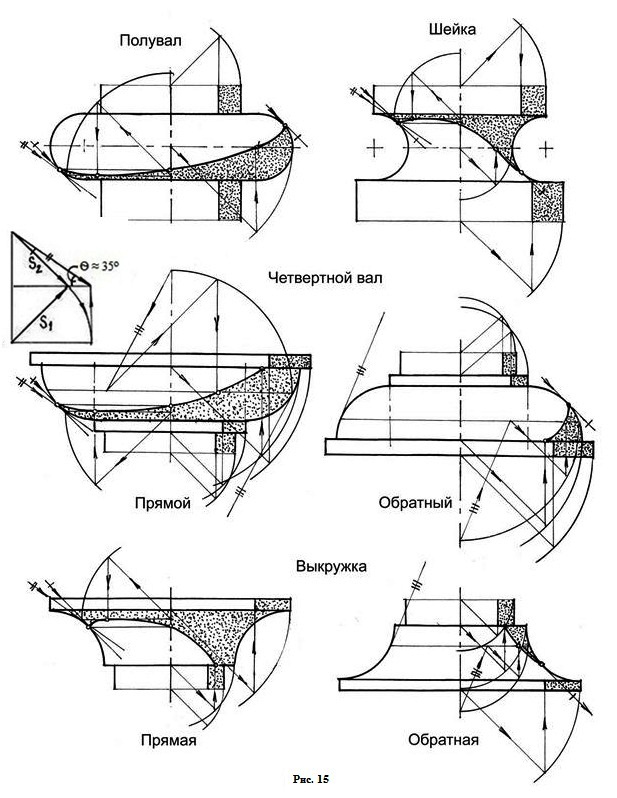
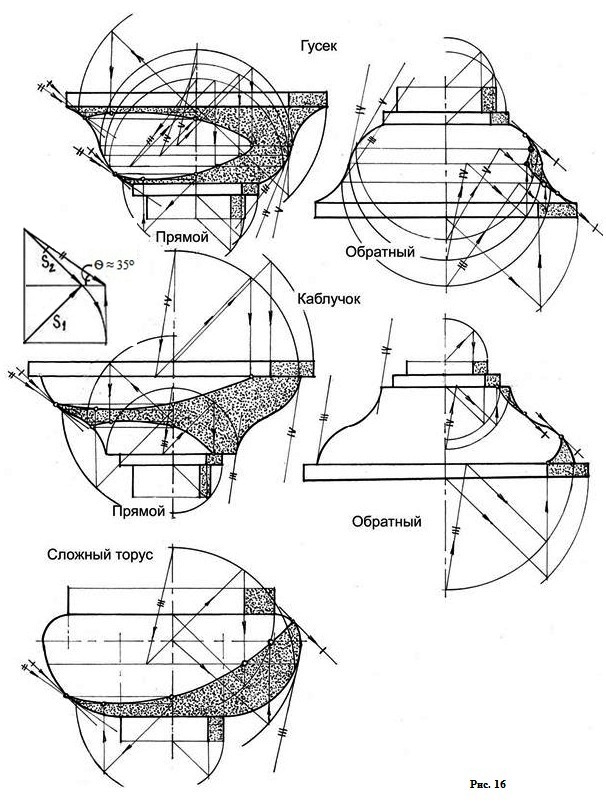
Примеры построения собственных теней на архитектурных обломах, которые образуют тела вращения (рис. 15, 16), приведены ниже.
Построение падающей тени от сферы на фронтальную плоскость
Падающие тени на фронтальную плоскость от поверхностей вращения можно построить с использованием продольного вспомогательного проецирования на вертикальную световую плоскость без применения второй (горизонтальной) проекции поверхности. На рис. 17 показано построение падающей тени от сферы на фронтальную плоскость, отстоящую от центра сферы на указанное расстояние m. При этом линией пересечения световой плоскости с фронтальной будет вертикальная прямая a, отстоящая на проекции от оси сферы на то же расстояние m.
Тени от высшей точки 12 и низшей точки 6 - точек контура собственной тени сферы, лежащих в световой плоскости, будут находиться на прямой а – это точки 12т² и 6т².
Симметричными точками контура собственной тени сферы относительно световой плоскости, будут точки, лежащие на одной горизонтальной прямой, например, точки 1 и 11. Чтобы построить тень 1т² от точки 1, следует из точки 11 провести луч света до пересечения с прямой d, а затем через точку пересечения – горизонтальную прямую до пересечения с лучом, проходящим через точку 1. Для построения тени 11т² от точки 11 следует провести горизонтальную прямую через точку пересечения прямой а с лучом 12т². При построении падающей тени 2т² от точки 2 нужно провести луч из точки 10 до пересечения с прямой а и из неё провести горизонтальную прямую до пересечения с лучом из точки 2. Точка тени 10т² строится с помощью горизонтальной прямой, проведенной через точку пересечения луча 2т² с прямой а и луча из точки 10. Так же строятся и другие точки эллипса падающей тени от сферы.
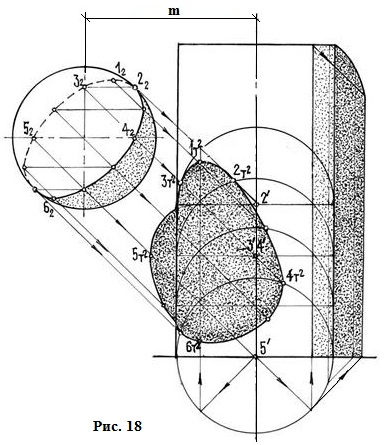На рис. 18 построены тени от сферы на поверхности вертикального цилиндра вращения. В этом случае тени от продольных проецирующих прямых зеркально повторяют форму плана, т.е. изображаются на цилиндре полуокружностями. Тени 1т² и 6т² от высшей и низшей точек собственной тени лежат на вертикальной образующей пересечения осевой световой плоскости с поверхностью цилиндра. Построение остальных точек тени можно проследить при определении точек 2т² и 3т² от симметричных относительно осевой плоскости точек 2 и 3. Для построения тени 2т² через точку 3 проведен луч света до пересечения с осью цилиндра в точке 3′, построена полуокружность с центром 3′, пересечение которой с лучом света, проведенным через точку 2, определит тень 2т². Тень 3т² – пересечение луча света 3т² с полуокружностью с центром 2′. Остальные точки тени построены аналогично.
Построение тени от вертикальной квадратной призмы на стену и цоколь здания.
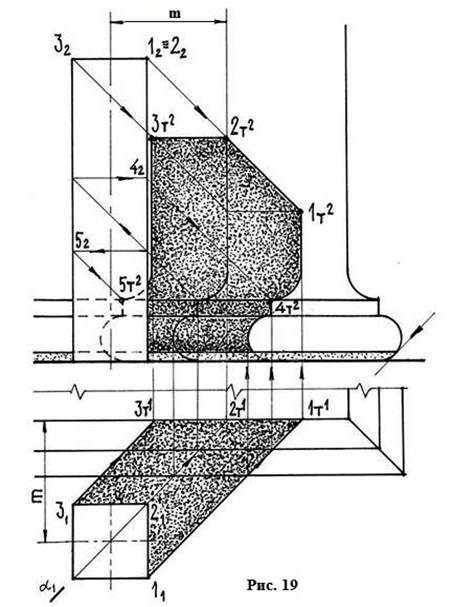
На рис. 19 показано, что тень от вертикальной прямой на продольные формы зеркально повторяет профиль последней. Световая плоскость α пересекает форму по линии, вертикально симметричной её профилю. Тень 2т² будет находиться на линии пересечения световой плоскости со стеной и цоколем здания, поскольку точка 2 находится в плоскости α. Тень 2т²3т² от продольного ребра 23 на вертикальную плоскость стены будет параллельна этому ребру. А тень 1т²2т² от глубинного ребра 12 совпадает с проекцией светового луча.
