Режекторные и селекторные фильтры.

Режекторный фильтр (фильтр-пробка) подавляет определенную частоту во входном сигнале. Он может быть спроектирован непосредственно по z-диаграмме.

Комплексная z-плоскость. Простейший режекторный фильтр типа НЦФ имеет один нуль на единичной окружности в z-плоскости в точке с частотой, которую необходимо подавить. Так, например, если из входного сигнала требуется исключить постоянную составляющую (нулевая частота), то импульсная реакция фильтра НЦФ имеет вид:

H(z) = 1-z. (9.3.1)

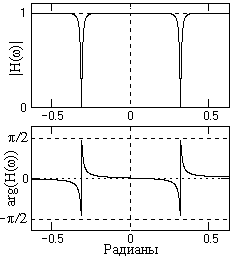
Нуль функции (9.3.1) равен n1=1. Как можно видеть на рис. 9.3.1, коэффициент передачи сигнала H(w) на любой частоте w_i от 0 до w_N=p/Dt - частоты Найквиста, определяемый выражением (9.3.1), будет равен длине вектора V_n1, проведенного из нуля функции H(z) - точка n1 на действительной оси, до соответствующей частоты w_i - точки z(w_i) на единичной окружности. На частоте w = 0 длина этого вектора равна нулю. Амплитудно-частотная характеристика фильтра, приведенная пунктиром на рисунке 9.3.2 для передаточной функции (9.3.1), далека от идеальной для фильтр-пробки.

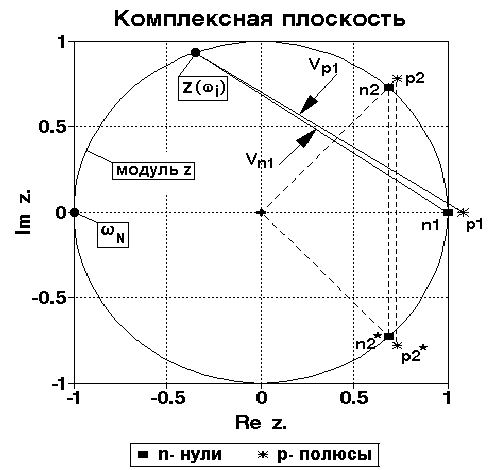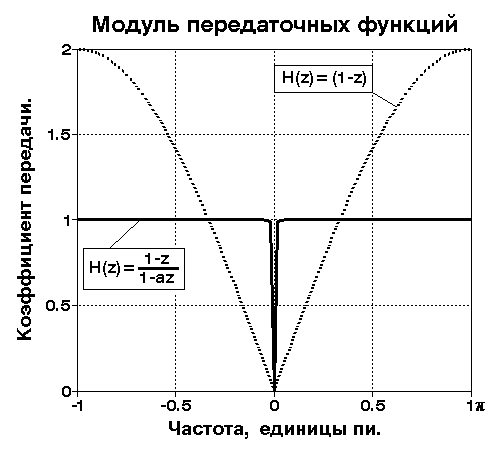Рис. 9.3.1. Синтез фильтров. Рис. 9.3.2. АЧХ фильтров.

Режекторный фильтр постоянной составляющей сигнала. Сконструируем простейший РЦФ, добавив к оператору (9.3.1) один полюс вне единичной окружности на малом расстоянии от нуля:

H_п(z) = G(1-z)/(1-az), z_p= 1/a. (9.3.2)

Допустим, что полюс помещен в точке p₁ = 1.01, при этом, а=0,99. Масштабный коэффициент G получим нормировкой H(z) к 1 на частоте Найквиста. Для приведенных условий G=0.995. Отсюда, при Dt=1:

H_п(z) = 0,995(1-z)/(1-0.99z),

y(k) = 0.995[x(k) –x(k-1)]+ 0.99y(k-1).

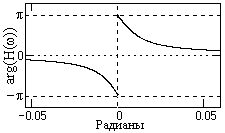Рис. 9.3.3.

Отображение нуля n₁ и полюса р₁ на z-плоскости и АЧХ фильтра для исключения постоянной составляющей приведены на рис.9.3.1. Коэффициент передачи сигнала на произвольной частоте w_i равен отношению длин векторов V_n1(z) и V_p1(z) соответственно из нуля и полюса до точки z(w_i) на единичной окружности и близок к единице для всех частот, за исключением нулевой:

|H_п(z)| = G V_n1(z)/V_p1(z).

Фазочастотная характеристика фильтра приведена на рис. 9.3.3 и определяется разностью фазовых углов векторов V_n1(z) и V_p1(z):

j_п(w) = j_n1-j_p1.

Режекторный фильтр произвольной частоты. При проектировании на подавление любой другой частоты w_v нули и полюсы располагаются на соответствующем радиусе z-плоскости. Радиальный угол направления на нуль и полюс определяются выражением:

j_v = p·w_v/w_N. (9.3.3)

Наличие двух знаков в выражении (9.3.3) отражает тот факт, что для получения вещественной функции фильтра нули и полюсы должны быть комплексно-сопряженными парами (их произведение дает вещественную функцию), т.е.:

H_v(z) = G(z-z_n)(z-z_n*)/[(z-z_p)(z-z_p*)]. (9.3.4)

Нули фильтра располагаются на единичной окружности:

z_n = cos j_v + j sin j_v = Re z_n + j Im z_n. (9.3.5)

Полюсы - на полярном радиусе R:

z_p = R cos j_v + j R sin j_v = Re z_p + j Im z_p. (9.3.6)

Пример положения нулей (n2 и n2*) и полюсов (р2 и р2*) приведен на рис.9.3.1. Подставляя (9.3.5-9.3.6) в (9.3.4), получаем:

H_v(z) = 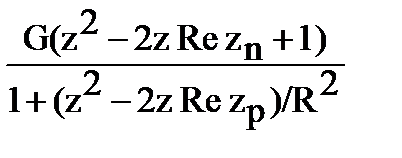, (9.3.7)

G = [1+(1+2Re z_p)/R²] / (2+2Re z_n). (9.3.8)

При приведении уравнения (9.3.7) в типовую форму:

H_v(z) = 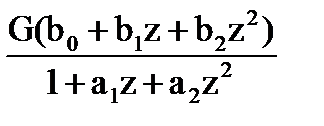, (9.3.7')

b₀ = 1, b₁ = -2·Re z_n, b₂ = 1. (9.3.9)

a₁ = - (2·Re z_p)/R², a₂ = 1/R².

Соответственно, алгоритм вычислений:

y(k) = G·[x(k) +b₁·x(k-1)+x(k-2)] – a₁·y(k-1) – a₂·y(k-2). (9.3.10)

Пример. Проведем расчет режекторного фильтра на частоту питания приборов f_s = 50 Гц, которая очень часто попадает в измеренные данные. Шаг дискретизации данных Dt = 0.001 сек.

Частота Найквиста: f_N = 1/2Dt = 500 Гц.

Радиальный угол на нули и полюса фильтра в z-плоскости: j = p·f_s/f_N = 0.1π.

Радиус полюса фильтра примем равным R = 1.01. Значения нуля и полюса:

z_n = cos j + j sin j = 0.951 + 0.309 j, z_p = R·cos j_v + j R·sin j_v = 0.961 + 0.312 j.

Значение масштабного множителя G по (9.3.8): G = 0.99.

Значения коэффициентов передаточной функции: b₁ = -2·Re z_n = -1.902,

a₁ = - (2·Re z_p)/R² = -1.883, a₂ = 1/R² = 0.98.

Частотная передаточная функция фильтра при подстановке коэффициентов в уравнение (9.3.7') и замене z = exp(-jω):

H(w) = 0.99[1-1.902·exp(-jω)+exp(-2jω)] / [1-1.883·exp(-jω)+0.98·exp(-2jω)].

Алгоритм фильтра: y(k) = 0.99[x(k) - 1.902 x(k-1) + x(k-2)] + 1.883 y(k-1) – 0.98 y(k-2).

Для проверки вычисленного в примере фильтра на рис. 9.3.4 приведен модельный входной сигнал, состоящий из суммы двух равных по амплитуде гармоник с частотой 50 и 53 Гц, и сигнал на выходе фильтра (смещен вверх). Справа на рисунке приведены спектры входного и выходного сигналов. Спектр выходного сигнала зарегистрирован после интервала установления реакции фильтра, который хорошо заметен на начальной части графика выходного сигнала. После установления сигнал на выходе фильтра практически полностью освобожден от гармоники 50 Гц.

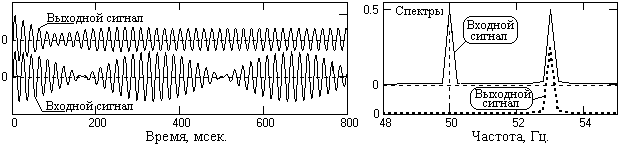
Рис. 9.3.4.

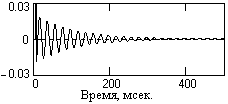Рис. 9.3.5.

При R → 1 ширина полосы подавления фильтра становится все более узкой, но при этом увеличивается длительность импульсной реакции фильтра и, соответственно, время установления фильтра при изменении спектра входного сигнала. В первом приближении значимая часть импульсной реакции режекторных фильтров равна (4÷5)/(R-1). Пример импульсной реакции для фильтра, вычисленного выше, приведен на рис. 9.3.5. Отклик фильтра получен при подаче на вход РЦФ импульса Кронекера. На графике не показан начальный пик отклика (отсчет на нулевой точке), амплитуда которого равна значению G.

Селекторный фильтр. Если в уравнении (9.3.4) опустить нули, то получим селекторный фильтр, выделяющий сигналы одной частоты ω_s – частоты селекции, с передаточной функцией:

H_s(z) = G/[(z-z_p)(z-z_p*)] = G1/(1+a₁z+a₂z²). (9.3.11)

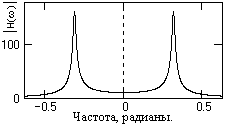Рис. 9.3.6.

Характер передаточной функции (9.3.11) можно представить непосредственно по z-плоскости (рис. 9.3.1). При расположении полюсов фильтра за пределами единичного круга (например, в точках р2 и р2*) значение коэффициента передачи фильтра на произвольной частоте ω на единичной окружности будет обратно пропорционально величине векторов из этих точек окружности на полюса фильтра. При изменении ω от нуля до ±π (движение по единичной окружности на z-плоскости по или против часовой стрелки) один из векторов (на полюс противоположной полуплоскости) изменяется в достаточно небольших пределах (не превышая значения 2), в то время как второй из векторов (на полюс в своей полуплоскости) будут сначала уменьшаться, достигает минимума при расположении ω на полярном радиусе полюса (на частоте селекции ω_s), а затем снова начинает увеличиваться. Соответственно, значение H_s(ω) максимально на частоте селекции ±ω_s и при R → 1 может быть очень высоким. Пример передаточной функции приведен на рис. 9.3.6.

При необходимости фильтр может быть пронормирован к 1 на частоте селекции определением значения G1 по условию H_s(ω) = 1 при ω = ω_s, т.е.:

G1 = 1+a₁ z(w_s)+a₂ z(w_s)².

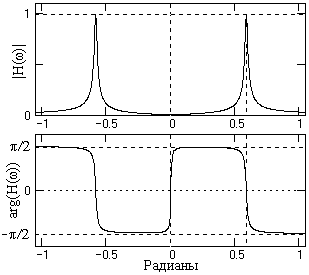Рис. 9.3.7.

Фильтр (9.3.11) в принципе не может иметь нулевого коэффициента передачи на других частотах главного диапазона. Если последнее является обязательным, то фильтр выполняется методом обращения режекторного фильтра H_v(z):

H_s(z) = 1-H_v(z).

H_s(z) = 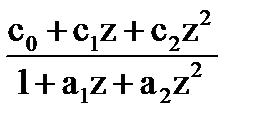. (9.3.12)

с₀ = 1-G, c₁ = a₁-Gb₁, c₂ = a₂-G.

Пример передаточной функции фильтра приведен на рис. 9.3.7. Пример применения фильтра для выделения гармонического сигнала на уровне шумов, мощность которых больше мощности сигнала, приведен на рис. 9.3.8.

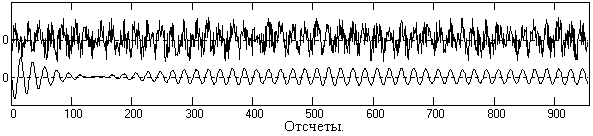Рис. 9.3.8. Фильтрация сигнала селекторным РЦФ.

Курсовая работа 11-07. Разработка программы расчета много- режекторных и селекторных рекурсивных цифровых фильтров и фильтрации цифровых сигналов.

Курсовая работа 12-07. Разработка программы расчета режекторных РЦФ повышенной добротности параллельной комбинацией режекторного РЦФ с двумя боковыми селекторными РЦФ и фильтрации цифровых сигналов.

Курсовая работа 13-07. Разработка программы расчета селекторных РЦФ повышенной добротности параллельной комбинацией селекторного РЦФ с двумя боковыми режекторными РЦФ и фильтрации цифровых сигналов.

Курсовая работа 14-07. Исследование дополнения интегрирующего фильтра Симпсона режекторным фильтром на частоту Найквиста и разработка программы обработки цифровых данных комбинированным фильтром.